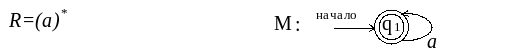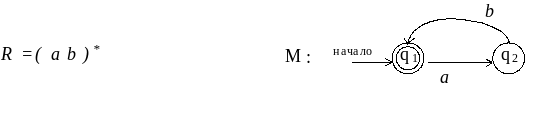Лекция 5 Характеристика процесса сканирования

Лексический анализ ( или сканирование) образует первый этап процесса компиляции. На этом этапе символы, составляющие исходную программу, считываются и группируются в отдельные лексические элементы, называемые лексемами. Лексический анализ важен для процесса компиляции по следующим причинам:

- замена в программе идентификаторов и констант лексемами делает представление программы удобнее для дальнейшей обработки;

- уменьшается длина программы, т.к. из нее устраняются несущественные пробелы и комментарии.

С точки зрения реализации процесса сканирования различают два подхода - прямой и непрямой лексический анализ. При прямом лексическом анализе требуется найти одну из многих лексем, которые заданы в описании данного языка.

Моделью прямого лексического анализатора служит множество работающих параллельно конечных автоматов (КА), каждый из которых распознает лексемы заданного типа. Эти КА можно представить и реализовать как один конечный преобразователь, моделирующий работу всех КА и выдающий сигнал о том, какой из них распознал очередную лексему.

При непрямом лексическом анализе требуется, прочитав цепочку символов, определить, образует ли эта цепочка лексему некоторого конкретного типа. В этом случае сканер работает вместе с синтаксическим анализатором, как некоторая программная процедура SCAN

Синтаксический анализатор обращается к SCAN всякий раз, когда ему нужен новый символ при анализе текста программы и построения ее внутреннего представления. В ответ на вызов, SCAN распознает очередную лексему в исходной программе и передает ее анализатору через таблицу лексем.

Непрямой сканер более экономичен ( в смысле экономии памяти), т.к. он не создает полной таблицы лексем для всего исходного текста программы.

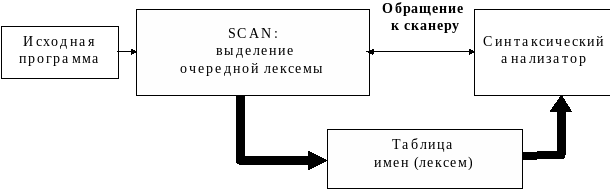
Рис.

Большинство лексем в языках программирования могут быть описаны в виде регулярных выражений, а так же соответствующих регулярных грамматик. Мы говорили о соответствии между регулярными грамматиками и КА. Практическое значение этого соответствия состоит в том, что для распознавания лексем, описываемых регулярными выражениями, можно использовать соответствующие КА.

Распознавание лексем выполняется следующим образом:

- входная цепочка считывается до тех пор, пока КА не достигнет заключительного состояния;

- по достижению заключительного состояния КА сигнализирует о нахождению лексемы данного типа и сканер заносит информацию о ней в таблицу имен (символов).

Таким образом, проблему построения непрямого лексического анализатора для данного типа лексем можно представить как проблему построения и реализации КА, который по достижению заключительного состояния, выдает на выходе лексему ( в этом смысле его можно рассматривать и как конечный преобразователь). В общем случае, такой КА является недетерминированным (НКА), однако, ,НКА можно преобразовать в эквивалентный ему детерминированный КА.

Рассмотрим способы описания лексем.

Построение недетерминированного конечного автомата по расширенному регулярному выражению

Рассмотрим теперь метод получения КА, распознающих лексемы языка, заданные регулярными выражениями.

Вход А1 : расширенное регулярное выражение R в алфавите  , не содержащее символа  и операций «  » «  ».

Выход А1 : недетерминированный КА (НКА) - М, для которого L(М)=R.

Описание А1: Получим автомат М₀ такой, что L(М₀)= R ₀ , выполняя рекурсивно следующие действия:

1. Если R₀=е, тогда М₀=( {q}  , , q, {q} ), где q - новое состояние;

2. Если R ₀ =а, где a , тогда М₀= ( {q₁,q₂}, ,₀ , q₁, {q₂} ), где ₀ (q₁,a) = {q₂}, в остальных случаях ₀ не определена; q₁ и q₂- новые состояния;

3. Если R₀=R₁| R₂, тогда применяем весь алгоритм к R₁ и R₂ и получаем соответственно М₁= ( Q ₁,, ₁, q₁, F₁ ) и

М₂=( Q₂ ,  , ₂, q₂ , F₂ ) , где Q₁ и Q₂ не пересекаются, а затем построим М₀=(Q₁Q₂ {q₀}, ,  ₀ ,q₀ ,F₀), где

а) q₀-новый символ;

б) ₀ включает ₁ и ₂, т.е. ₀ (q₀ ,a)= ₁ (q₁ ,a) ₂ (q₂ ,a);

в) F₀=F₁F₂ , если q₁ F₁ и q₂ F₂ , в противном случае F₀ =F₁F₂ { q₀ }.

4. Если R₀=R₁ R₂ , то применим весь алгоритм к R₁ и R₂ и получим М₁ и М₂ , как в п.3 .Построим М₀=(Q₁  Q₂ , , ₀ , q₁, F₀ ) , где

а) ₀ включает ₂ ; ₀ (q ,a)= ₁ (q ,a) для всех q  Q и a   , если q  F₁, и ₀ (q ,a)= ₁ (q ,a)  ₂ (q₂ ,a) в противном случае;

б) F₀=F₂ , если q₂  F₂ , и F₀=F₁ F₂ в противном случае.

5. Если R₀=R₁^* , то применим весь алгоритм к R₁ и получим М₁=( Q₁ ,, ₁ , q₁ , F₁).

Построим М₀=( Q₁  {q₀}, , ₀ , q₀ , F₁ {q₀}), где q₀ - новый символ и ₀ определяется соотношениями:

а) ₀ (q₀ ,a)=₁ (q₁ , a);

б) если q  F₁ , то ₀ (q ,a)=₁ (q ,a);

в) если q  F₁ , то ₀ (q ,a)=₁ (q,a)  ₁ (q₁ , a).

6. Если R₀=R₁⁺ , то применим весь алгоритм к R₁ и получим М₁, как в п.5. Построим М₀=( Q₁, , ₀ , q₁ ,F₁), где ₀ (q,a)=₁(q,a), если q  F₁ , и ₀ (q ,a)=₁ (q ,a) ₁ (q₁ ,a), если q  F₁.

7. Если R₀=R₁^*n, то применим весь алгоритм к R₁ и получим М₁ , как в п.5. Построим М₀ =(Q₁ {1,..., n}, , ₀ , [q₁ ,1], F₀), где

а) если q  F₁ или i=n, то ₀ ([q ,i], a )={[p , i] |₁ (q ,a) содержит p};

б) если q  F₁ и i<n, то ₀ ( [ q , i ] , a)={ [p , i] | ₁( q , a) содержит p}U{ [p ,i +1] | ₁(q₁ ,a) содержит p }

в) F₀={ [q , i ] | q  F₁ , 1  i  n } U { [q₁ ,1] }.

8. Если R₀=R₁⁺ⁿ , выполним то же , что и в (7) , но пункт (7,в) заменим на F₀={ [q , i ] | q  F₁ , 1 i  n }.

Пример . Пусть R = (0 | 1) , преобразуем его в НКА :

1. R можно представить как R = (R₁ | R₂) , где R₁ = 0 , R₂ .

2. Применяя п. 2 для R₁ и R₂ , получаем :

3. Применяя п. 3 к R = (R₁ | R₂), объединяем состояния автоматов М₁ , М₂ и получаем результирующий автомат М

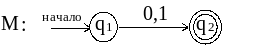
Пример . Пусть R = (0 | 1)^* , преобразуем его в НКА :

1. Используя результаты , полученные в примере 4.2, и применяя п.5 для R , получим автомат М:

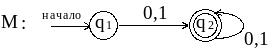
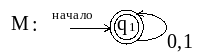
2. Согласно п. 5 , объединяем q₁ и q₂ и получаем

Пример . Пусть R = (a | b) (a | b |0 | 1)^* , выполним его преобразование в НКА :

1. Представим r как R = R₁ R₂ ,

где R₁ = (R₃ | R₄) , R₂ = ( )^* , R₃ = a , R₄ = b ;

= (R₅ | R₆ | R₇ | R₈) , R₅ = a , R₆ = b , R₇ = 0 , R₈ = 1 ;

2. Автоматы , соответствующие выражениям R₁ и R₂ легко получить , используя результаты примеров 4.2 , 4.3. Для R₁ получим

для R₂

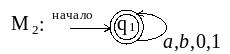
3. Применяем п. 4 к выражению R = R₁ R₂ и получаем результирующий автомат М:

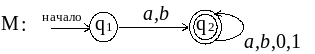
Пример Пусть R = (00 | 11)^* , преобразуем его в НКА :

1. Представим R следующим образом :

R = R1* , R1 = R2 | R3

R2 = R4 R5 , R3 = R6 R7 ,

R4 = 0 , R5 = 0, R6 = 1 , R7 = 1

2. Для R₂ и R₃ применяем пп. 2 и 4 ( можно использовать результаты предыдущих примеров ) и получаем автоматы М₂ и М₃ :

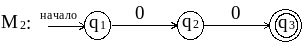
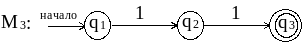
3. Применяя п. 3 к R₁ = R₂ | R₃ , получаем из М₂ и М₃ результирующий автомат М₁ :

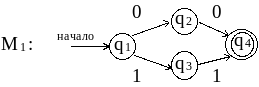
4. Применяя п. 5 к R = R₁^* , получаем из М₁ автомат М

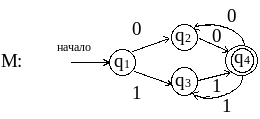
Для того, чтобы лучше усвоить и закрепить навыки преобразований, полученные в этих примерах, и использовать их в дальнейшем, приведём соответствия между некоторыми простыми регулярными выражениями и КА:
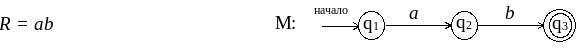
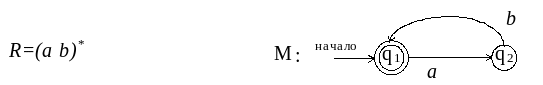
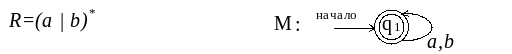