Свойства.

1. - наивысшая степень точности.

Покажем что в случае условие теоремы не выполняется:

Для любого многочлена степени

.

2. Узлы симметричны на .

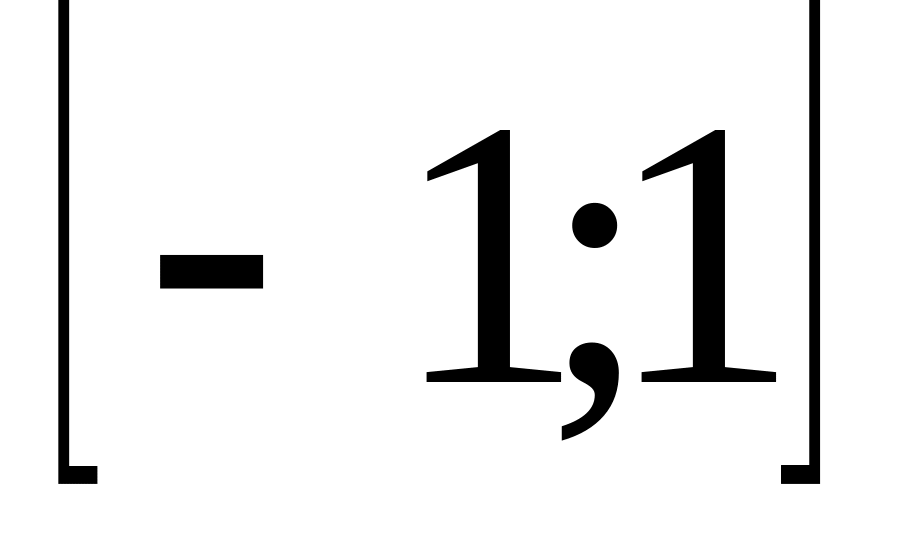3. все коэффициенты 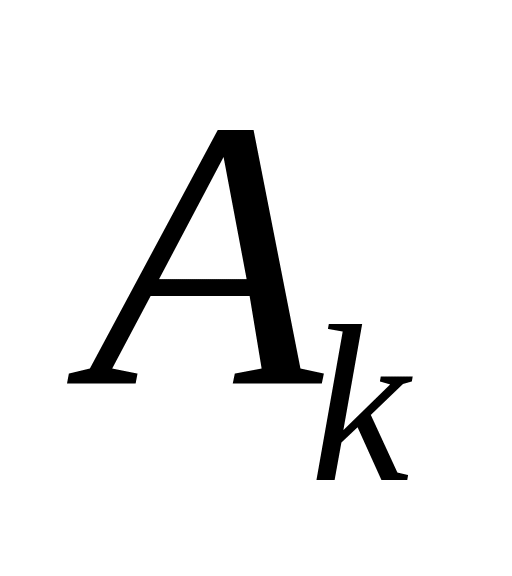положительны и для симметричных узлов равны.

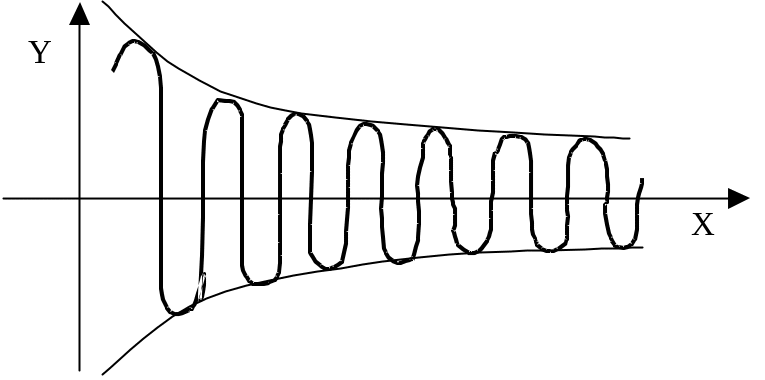
34 Интегрирование быстроосциллирующих функций.

Осцилляция – быстрое изменение знака. При возрастании числа осцилляция усиливается. Рассмотрим 2 интеграла:

Потребуем, чтобы эти интегралы сходились, для этого функция должна убывать быстрее, чем функция , т.е. ,

где и - некоторые константы больше нуля. Формулы Ньютона-Котеса работают для осцилляционных функций плохо. Выведем квадратурные формулы для интегралов таких типов. Возьмем в качестве весовой функции: . Рассмотрим функцию на конечном интервале : .

Заменим функцию многочленом Лагранжа. Тогда аналогично будем иметь, что

(1)

С ростом числа - степени многочлена, числа узлов, подсчет по формулам (1) затруднителен. Рассмотрим маленький отрезок длины шага . Тогда многочлен есть линейная функция:

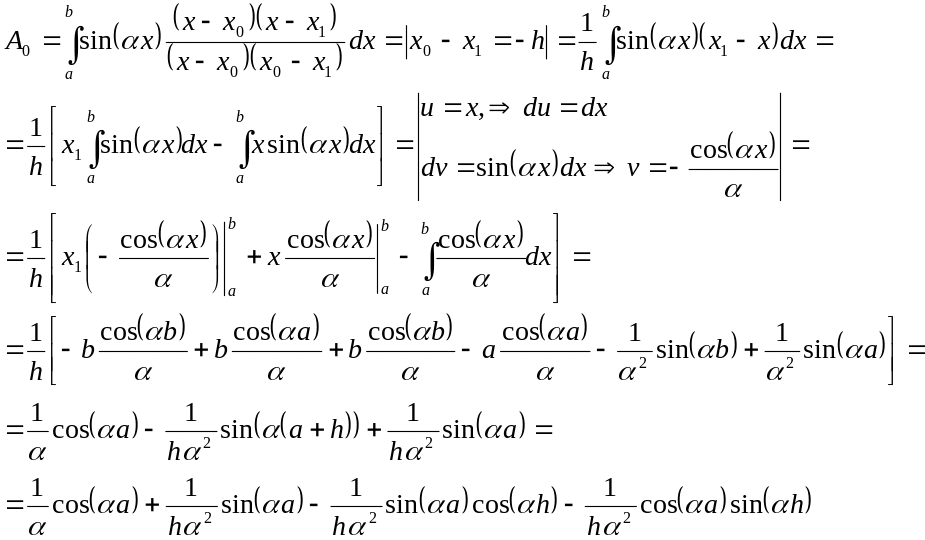
Следовательно

Аналогично

Теперь разобьем на интервалов, на каждом из которых применим полученные формулы. Получим в общем, виде:

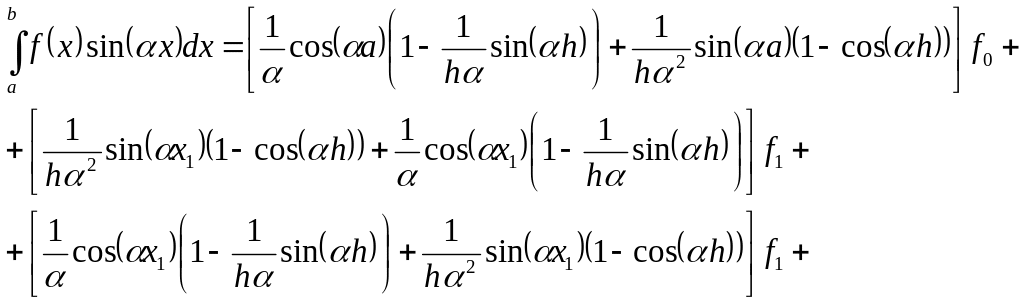
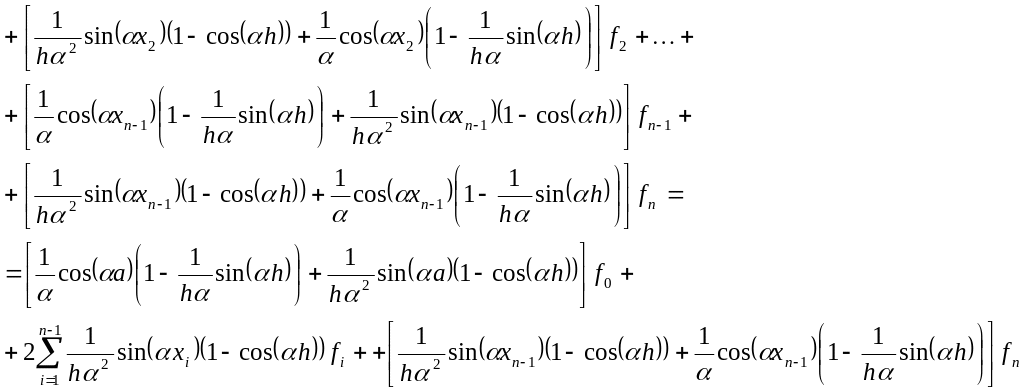
Представим первоначальный интеграл в следующем виде:

так как , то . Таким образом, формула для синус–преобразования выглядит так:

Аналогично получим формулу для косинус–преобразования:

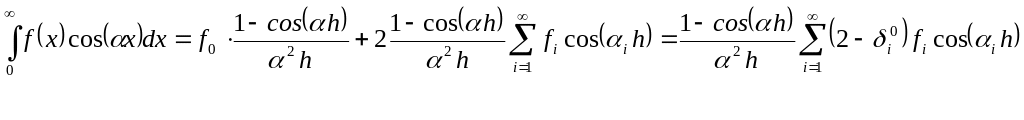
36-41 Общ. часть

Численные методы решение задач Коши для обыкновенных дифференциальных уравнений (д. у.).

Будем рассматривать д. у. следующего вида : . Т.е. требуется найти решение уравнения у=f(x,y), вида у=у(х), удовлетворяющее условию у(х₀)=у₀. Функций, удовлетворяющих уравнений (1) много, но лишь одна из них проходит через точку (х₀, у₀). Для несложных функций f(x,y) решение такой задачи может быть найдено аналитически.

Существование и единственность задачи Коши дается в теореме Пикара.

Теорема Пикара: если функция f(x,y) определена в некоторой области G={(x,y): |x-x₀|a, |y-y₀|b} и по переменной у удовлетворяет условию Липщица: |f(x,y₁)-f(x,y₂)|L|y₁-y₂|, L – const Липшица, то на некотором отрезке |x-x₀| h, h>0 существует и единственно решение задачи Коши (1)-(2).

Если функция f(x) – дифференцируемая, ограничена и по у имеет производную, то в качестве const Липшица можем взять: L= | |. Рассмотрим несколько методов нахождения решения задачи Коши.

36 Метод Пикара.

Основан на расщеплении функции f(x).

Пусть f(x) представляется в виде суммы двух функций: f(x,y)=f₁(x,y)+f₂(x,y). Таких, чтобы задача Коши с функцией f₁ могла бы иметь решение, а функция f₂ должна быть достаточно малой функцией. Т.е., чтобы задача Коши: (3) была разрешима для любой функции g.

Если имеет место (3), то можно построить итерационный процесс для решения задачи (1)-(2). Этот итерационный процесс называется итерационным процессом Пикара. Построим его по следующему правилу:

Возьмем у⁰(х)=у(х₀)=у₀ за начальное приближение.

, =g(x) - решением этой новой задачи Коши является функция у¹(х).

, = g(x) - решением этой новой задачи Коши является функция у²(х).

(4) решением этой задачи Коши является функция у^к+1(х).

Самый простой вариант метода Пикара – когда f₁1, f₂=f, тогда задача Коши (4) имеет следующий вид: у⁽⁰⁾=у₀

(5)

проинтегрируем уравнение задачи Коши (5) от х₀ до х:

(y^(k+1))dx= f(x,y ^(k) (x))dx y^(k+1)(x)=y^(k+1)(x₀)+ f(x,y^(k)(x))dx

Решение задачи Коши – интеграл. Вычисление таких интегралов затрудняет процесс вычисления.

(7) - формула Пикара. Выясним сходимость метода:

- функциональная последовательность.

|y^(k+1)(x)-y^(k)(x)|=| - |=| -

- |=| [f(x,y^(k))-f(x, y^(k-1))]dx| | f(x,y^(k))-f(x, y^(k-1))|dx

{для f применим неравенство Липшица} L |y^k(x)-y^k-1(x)|dx

Т.е. разность на к-том шаге может быть определена через разность на (к-1)-м шаге. Оценим модуль разности при к=1:

|y¹(x)-y⁰(x)| {A= }A(x-x₀)

оценим при к=2:

|y²(x)-y¹(x)| L |y¹-y⁰|{A= }AL (x-x₀)dx=AL =

= L²

оценим при к=3:

|y³(x)-y²(x)| L |y²-y¹|{A= }AL² dx=

= L² (x-x₀)³= L³

в итоге получим: | y^k+1(x)-y^k(x)| L^(k+1)

L^(k+1) - это (к+1)-й член ряда Тейлора для функции . Ряд сходится и его (к+1)-й член стремится к нулю при к. Следовательно с увеличением шага итераций к | y^k+1(x)-y^k(x)|0.

Т.о. метод Пикара сходится.

Замечание: при малых величинах L(x-x₀)0.1;0.01 метод Пикара достаточно быстро сходится, решение можно получить за 5-10 итераций с 15-ю точными знаками после запятой

Интегралы в формуле вносят погрешность.