
Приближённые вычисления.
По данной теме сначала изучите § 1 – 4 гл. 1 [2] или § 1 – 5 гл. 1 [7]. Внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [2], гл. 1, № 1.2 – 1.20 (чётные) или [7], гл. 1, № 1 (6 – 9), 3, 4, 6 – 16.
При сложении и вычитании приближённые вычисления рекомендуется выполнять так:
а) выделить слагаемое с наименьшим числом верных десятичных знаков;
б) округлить остальные слагаемые так, чтобы каждое из них содержало на один десятичный знак больше, чем выделенное;
в) выполнить действие, учитывая все сохранённые десятичные знаки;
г) результат округлить и сохранить столько десятичных знаков, сколько их в приближённом числе с наименьшим числом десятичных знаков.
Пример 1. Вычислить сумму приближённых чисел 0,6, 0,42 и 0,286. Найти границу погрешности результата.
Решение. Округлим все данные, сохранив два десятичных знака, и выполним сложение: 0,6 + 0,42 + 0,286 ≈ 0,6 + 0,42 + 0,29 = 1,31 ≈ 1,3.
При умножении и делении приближённые вычисления рекомендуется выполнять в следующем порядке:
а) выделить исходное данное с наименьшим числом верных значащих цифр;
б) округлить остальные данные так, чтобы каждый из них содержало на одну значащую цифру больше, чем в выделенном;
в) выполнить действия, учитывая все сохранённые значащие цифры;
г) сохранить в результате столько значащих цифр, сколько имеет исходное данное с наименьшим числом верных значащих цифр.
Пример 2. Найти частное приближённых чисел 654,1 и 8,5 и границу погрешности результата.
Решение. Округлим делимое, сохранив три значащие цифры, т. е. до единиц: 654,1 ≈ 654. Выполним деление и оставим в результате две значащие цифры: 654,1 : 8,5 ≈ 654 : 8,5 ≈ 76,9 ≈ 77.
КОМПЛЕКСНЫЕ ЧИСЛА.
Основные понятия и определения. Решение многих задач сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов математики. Стремление сделать уравнения разрешимыми – одна из главных причин расширения понятия числа.
Так, для разрешимости уравнения x +a=b положительных чисел недостаточно и приходится вводить отрицательные числа и нуль.
Для решения уравнения ax = b (a≠0) недостаточно целых чисел и приходится вводить дробные числа. Целые и дробные числа образуют множество Q рациональных чисел.
На множестве рациональных чисел разрешимы уравнения вида ax=b (a≠0), однако уравнение x2=2 не имеет рациональных корней. Необходимость решения таких уравнений явилась одной из причин введения иррациональных чисел.
Рациональные и иррациональные числа образуют множество R действительных чисел.
Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение x2+1=0 не имеет действительных корней. Поэтому приходится расширять множество действительных чисел до нового множества, такого, чтобы в этом множестве уравнения вида x2+a2=0 имели решение.
Корень уравнения x2+1=0 или x2= - 1 называется мнимой единицей и обозначается буквой i.
Таким образом, символ i удовлетворяет условию i2= - 1.
Комплексным числом называется выражение вида a+bi, где a и b – действительные числа, а i – мнимая единица.
Число а называется действительной частью комплексного числа, а число bi – мнимой частью.
Комплексное число часто обозначают одной буквой z.
Множество комплексных чисел принято обозначать буквой С.
Запись комплексного числа в виде z=a+bi называется алгебраической формой записи комплексного числа.
Два комплексных числа a1+b1i и a2+b2i называются равными тогда и только тогда, когда a1=a2 и b1=b2, т. е. когда равны их действительные части и коэффициенты при мнимой части.
Понятия «больше» и «меньше» для комплексных чисел не определяются.
Комплексное число z = 0 + 0i называется нулём и обозначается 0; комплексное число z = a +0i отождествляется с действительным числом а, т. е. a + 0i = a; комплексное число z = 0 + bi называется чисто мнимым и обозначается bi, т. е. 0 + bi = bi.
Число 0 является единственным числом, которое одновременно и действительное, и чисто мнимое.
Комплексные числа a + bi и a - bi называются сопряжёнными.
Действия над комплексными числами в алгебраической форме. Суммой двух комплексных чисел z1 = a1 + b1i и z2 =a2 ± b2i называется комплексное число z1 + z2 = (a1 + a2) + (b1 + b2)i.
Произведением двух комплексных чисел z1 = a1 + b1i и z2 = a2 + b2i называется комплексное число z1z2 = (a1a2 - b1b2) + (a1b2 + a2b1)i.
Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел z2 = a2 + b2i и z1 = a1 + b1i определяются формулами:
Z2 - z1 = (a2 - a1) + (b2 - b1)i
![]() =
= ![]() +
+ ![]() i,
i,
где a1+b1i ≠0+ 0i.
Формулы, определяющие правила действий над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия над двучленами a1+b1i и a2+b2i и заменить i2 на -1.
При
делении на комплексное число достаточно
умножить числитель и знаменатель дроби
![]() на
число, сопряжённое знаменателю, т. е. на
a1-
b1i.
на
число, сопряжённое знаменателю, т. е. на
a1-
b1i.
Возведение комплексного числа в степень производится по формулам возведения двучлена в степень, но при этом надо учитывать, что:
СТЕПЕНИ i
i1= i, i4n+1= i1= i,
i2= - 1, i4n+2= i2= - 1,
i3= - i, i4n+3= i3= -i,
i4= 1, i4n= 1.
Например, i24=1, i59=i4 ∙ 14+3=i3=−i, i42= i4∙10+2= i2=−1.
Пример 1. Найти сумму и произведение комплексных чисел z1= 2-7i и z2= 3+5.
Решение. Сумму находим формальным сложением двучленов 2-7i и 3+5i:
z1+z2= (2-7i) = (3+5i) = 2-7i+3+5i= 5-2i.
Произведение находим формальным перемножением двучленов 2-7i и 3+5i с последующей заменой i2 на -1:
z1z2= (2-7i) (3+5i) = 6-21i+10i-35i2 = 6-11i+35 = 41-11i.
Пример 2. Даны комплексные числа z1 = 3-4i и z2 = 10+5i. Найти разность и частное z2-z1 z2/z1.
Решение. Разность находим формальным вычитанием двучленов 10+5i и 3-4i:
z2-z1 = (10+5i) – (3-4i) = 10+5i-3+4i = 7=9i.
Чтобы найти частное z2/z1 , умножим числитель и знаменатель этой дроби на число, сопряжённое знаменателю z1:
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() = 0,
4+2, 2i.
= 0,
4+2, 2i.
Пример
3.
Найти комплексное число z
= ![]() .
.
Решение. Выполнив в знаменателе дроби возведение в степень, получим
Z
= ![]() =
= ![]() =
= ![]() .
.
Умножив числитель и знаменатель полученной дроби на число, сопряжённое знаменателю, т. е. на -5-12i, получим
Z
= ![]() =
= ![]() =
= ![]() =
= ![]() = -i.
= -i.
Геометрическая интерпретация комплексного числа. Комплексные числа, как и действительные, допускают простую интерпретацию, если вместо координатной прямой использовать координатную плоскость.
Комплексное
число z
= a+bi
изображается на координатной плоскости
точкой M
(a,
b)
или вектором ![]() ,
начало которого совпадает с началом
координат, а конец – с точкой M
(рис. 1).
,
начало которого совпадает с началом
координат, а конец – с точкой M
(рис. 1).







Рис. 1 Рис. 2






Рис. 3
Сама координатная плоскость называется при этом комплексной плоскостью, ось абсцисс – действительной осью, а ось ординат – мнимой осью.
Модулем
комплексного
числа называется абсолютная величина
вектора, соответствующего этому числу.
Для модуля числа z
= a+bi
используются обозначения r,
![]() или
или ![]() .
.
На основании теоремы Пифагора (рис. 1) получается формула
= r
= ![]() .
.
Например, комплексное число z = 8-6i имеет модуль, равный 10, так как
= ![]() =
= ![]() =
= ![]() = 10.
= 10.
Аргументом
комплексного числа z≠0
называется величина угла
![]() между
положительным
направлением действительной оси и
вектором, соответствующим этому числу
(рис. 1).
между
положительным
направлением действительной оси и
вектором, соответствующим этому числу
(рис. 1).
Для
аргумента числа z
= a+bi
используются обозначения
![]() ,
arg
z
или arg
(a+bi).
,
arg
z
или arg
(a+bi).
Аргумент комплексного числа z≠0 в отличие от модуля определяется не однозначно.
Так,
аргументами числа 5 являются следующие
углы: ![]() =
0,
=
0, ![]() =2
=2![]() ,
,
![]() =
-2
и вообще каждый из углов
=
-2
и вообще каждый из углов ![]() =
2
=
2![]() ,
k
,
k![]() Z;
аргументом числа 3i
– следующие углы:
=
Z;
аргументом числа 3i
– следующие углы:
=
![]() ,
=
+2
,
=
- 2
(рис. 2) и вообще каждый из углов
=
+ 2
k,
k
Z.
,
=
+2
,
=
- 2
(рис. 2) и вообще каждый из углов
=
+ 2
k,
k
Z.
Любые два аргумента комплексного числа отличаются друг от друга на слагаемое, кратное 2 .
Аргумент комплексного числа z = a+bi можно находить так:
а)
найти острый угол ![]() =
arctg
=
arctg
![]() ;
;
б)
найти аргумент комплексного числа в
зависимости от того, в какой координатной
четверти лежит вектор, соответствующий
этому числу: в ı
четверти
=
;
во ıı
четверти
=
–
;
в ııı
четверти
=![]() ;
в ıv
четверти
;
в ıv
четверти
![]() .
.
Пример
4. Найти
аргумент комплексного числа z
= 1 – i
![]() .
.
Решение.
Находим угол
= arctg
![]() = arctg
=
/3.
Вектор, соответствующий данному
комплексному числу, лежит в ıv
координатной
четверти (рис. 3), поэтому аргументами
числа являются каждый из углов
= 2
-
= arctg
=
/3.
Вектор, соответствующий данному
комплексному числу, лежит в ıv
координатной
четверти (рис. 3), поэтому аргументами
числа являются каждый из углов
= 2
- ![]() + 2
k
=
+ 2
k
= ![]() + 2
,
k
Z.
+ 2
,
k
Z.
Аргументы действительных и чисто мнимых чисел надо находить непосредственно, исходя из их геометрической интерпретации, а не используя приведённое выше правило (тем более, что для чисто мнимых чисел это правило вообще нельзя применять).
Тригонометрическая
форма комплексного числа.
Пусть дано комплексное число z
= a
+ bi.
Из ![]() OMA
(см. рис. 1) можно выразить действительные
числа a
и b
через модель r
и аргумента
числа z
следующим образом: a
= r
cos
,
b
= r
sin
.
Таким образом, комплексное число можно
записать в виде
OMA
(см. рис. 1) можно выразить действительные
числа a
и b
через модель r
и аргумента
числа z
следующим образом: a
= r
cos
,
b
= r
sin
.
Таким образом, комплексное число можно
записать в виде
Z = r (cos + i sin ),
где r – модуль комплексного числа, а - один из его аргументов. Представление комплексного числа z ≠ 0 в указанном виде называется тригонометрической формой записи комплексного числа.
Для
того чтобы перейти от алгебраической
формы записи комплексного числа z
= a
+ bi
к тригонометрической, достаточно найти
его модуль и один из аргументов. Аргумент
комплексного числа z
= a
+ bi
можно находить и из системы ![]()
Пример 5. Записать число z = - - i в тригонометрической форме.
Решение. Находим модуль
r
= ![]() =
= ![]() =
= ![]() = 2.
= 2.
Находим угол
![]() = arctg
= arctg ![]() = arctg
= arctg ![]() = arctg
= arctg ![]() =
= ![]() .
.
Вектор,
соответствующий данному комплексному
числу, лежит в ııı
координатной четверти ( рис. 4), поэтому
одним из аргументов является
= ![]() +
=
+
= ![]() .
Следовательно
,
.
Следовательно
,
Z
= -
![]() - i
= 2 ( cos
+ i
sin
).
- i
= 2 ( cos
+ i
sin
).
Для того чтобы перейти от тригонометрической формы записи комплексного числа z = r (cos + i sin ) к алгебраической, достаточно найти действительные числа a и b по формулам a = r cos , b = r sin .



Рис. 4
Пример
6. Записать
число z
= 2 (cos
![]() + i
sin
)
в алгебраической форме.
+ i
sin
)
в алгебраической форме.
Решение. Сначала найдём cos и sin :
cos
= cos (![]() )
= cos
)
= cos ![]() =
=
![]() ,
,
sin
![]() = sin (
)
= - sin
=
-
= sin (
)
= - sin
=
- ![]() .
.
Тогда
a
= 2 (![]() )
=
,
b
= 2 (- 1/2 ) = - 1. Следовательно, z
= 2 (cos
+ i
sin
)
=
- i.
)
=
,
b
= 2 (- 1/2 ) = - 1. Следовательно, z
= 2 (cos
+ i
sin
)
=
- i.
Действия над комплексными числами, заданными в тригонометрической форме. Если z1 = r1 (cos + i sin ) и z2 = r2 (cos 2 + i sin 2), то
z1z2 = r1r2 (cos ( 1 + 2) + i sin ( 1 + 2)),
![]() =
=
![]() (cos (
(cos (![]() )
+ i sin (
)).
)
+ i sin (
)).
Если z = r (cos + i sin ), то
zn = (r (cos + i sin ))n = rn (cos n + i sin n ),
![]() =
= ![]() =
= ![]() (cos
(cos ![]() )
)
где
![]() - арифметический корень, k
= 0, 1, 2, ..., n
– 1.
- арифметический корень, k
= 0, 1, 2, ..., n
– 1.
Пример
7.
Даны комплексные числа z1
= 12 (cos
2250
+ i
sin
2250)
и z2
= ![]() (cos
750
+ i
sin
750).
Найти их произведение z1z2
и частное z1/z2.
Ответ записать в алгебраической форме.
(cos
750
+ i
sin
750).
Найти их произведение z1z2
и частное z1/z2.
Ответ записать в алгебраической форме.
Решение. Применяя правила умножения и деления комплексных чисел, имеем
z1z2
= 12∙
![]() (cos
(2250
+ 750)
+ i sin (2250
+ 750))
= 18 (cos 3000
+ i sin 3000)
=18(
- i
)=
9
– 9i
;
(cos
(2250
+ 750)
+ i sin (2250
+ 750))
= 18 (cos 3000
+ i sin 3000)
=18(
- i
)=
9
– 9i
;
![]() = 12:
(cos
(2250
– 750)
+ i sin (2250
– 750))
= 8 (cos 1500 + i sin 1500) = 2 (-
+ i
= 12:
(cos
(2250
– 750)
+ i sin (2250
– 750))
= 8 (cos 1500 + i sin 1500) = 2 (-
+ i ![]() )
= -
4
+ 4i.
)
= -
4
+ 4i.
Пример 8. Вычислить z = (2(cos 240 + i 240))5.
Решение. Находим
Z = 25 (cos 5∙240 + i sin 5∙240) = 32 (cos 1200 + i sin 1200) = 32 (- + i ) = - 16 + 16i .
Пример 9. Вычислить ( - i )10.
Решение. Запишем число – i в тригонометрической форме. Находим
 r
=
r
= ![]() =
=
= 2,
=
=
= 2,
= arctg
![]() = arctg
= arctg
=
,
= arctg
= arctg
=
,
= 2
-
=
![]() или
= 3300.
или
= 3300.
Тогда - i = 2 (cos 3300 + i sin 3300) и, значит,
z = (2 (cos 3300 + i sin 3300))10 = 210 (cos 33000 + i sin 33000) = 210 (cos (600 + 9∙3600) +
+ i sin (600 + 9∙3600) + i sin (600 + 9∙3600)) = 210 (cos 600 + i sin 600) = 1024 ( + i )= 512 + 512i .
Пример
10.
Вычислить ![]() .
Ответ записать в тригонометрической и
алгебраической формах.
.
Ответ записать в тригонометрической и
алгебраической формах.
Решение. Запишем число – 81 в тригонометрической форме: - 81 = 81 (cos + i sin ). Следовательно,
= ![]() =
= ![]() (cos
(cos
![]() + i
sin
)
=
+ i
sin
)
=
=
3 (cos
(![]() )
+ i sin (
)),
где
k = 0, 1, 2, 3.
)
+ i sin (
)),
где
k = 0, 1, 2, 3.
При k = 0, 1, 2, 3 получим:
Z0
= 3 (cos
![]() + i sin
)
= 3 (
+ i sin
)
= 3 (![]() )
=
)
= ![]() ;
;
Z1
=
3 (cos
(![]() )
+ i sin (
))
= 3 (-
)
+ i sin (
))
= 3 (-
![]() )
= -
)
= - ![]() +
+ ![]() ;
;
Z2
= 3 (cos
(![]() )
+ i sin (
))
= 3
(
)
+ i sin (
))
= 3
(![]() )
= -
)
= - ![]() ;
;
z3
= 3 (cos
(![]() )
+ i sin (
))
= 3 (
)
+ i sin (
))
= 3 (![]() )
=
.
)
=
.
Показательная форма комплексного числа. Рассматривая функцию y = ex для комплексного переменного, Эйлер установил замечательное соотношение
![]() =
cos
+ i sin
,
=
cos
+ i sin
,
которое называется формулой Эйлера.
Из этой формулы следует, что каждое комплексное число Z≠0 можно записать в форме
Z
=
r (cos
+ i sin
)
= ![]() ,
,
которая называется показательной формой записи.
Над комплексными числами, заданными в показательной форме, удобно производить умножение и деление, возведение в натуральную степень и извлечение корня:
r1
![]() r2
r2
![]() = r1
r2
= r1
r2
![]() ;
;
![]() =
= ![]() ;
;
(reiφ)n
=
![]() ;
;
![]() ,
k = 0, 1, 2, ... , (n – 1).
,
k = 0, 1, 2, ... , (n – 1).
Пример
11.
Представить число
![]() в
алгебраической форме.
в
алгебраической форме.
Решение.
По условию, r
= 4,
=
![]() ,
откуда
,
откуда
a
= 4 cos ![]() ,
,
b
= 4 sin ![]() .
.
Значит,
z
= 4![]() .
.
Пример 12. Выполнить действия и записать ответ в тригонометрической и показательной формах:
Z
= 10 (![]() ).
).
Решение. Сначала выполним действия:
Z
= 10 (![]() )
= 10
(
)
= 10
(![]() )
=
)
=
=
10 (![]() )
=
10
)
=
10
![]() =
=
![]() =
3 + 3i.
=
3 + 3i.
Теперь запишем число в тригонометрической и показательной формах, для чего найдём его модуль и аргумент:
r
= ![]() ,
,
= ![]() .
.
Тогда
z
= 3![]() ,
z
= 3
,
z
= 3![]() .
.
ВЕКТОРЫ И КООРДИНАТЫ НА ПЛОСКОСТИ.
Понятие вектора. Некоторые физические величины (сила, скорость, ускорение и др.) характеризуются не только числовым значением, но и направлением. Например, для того чтобы охарактеризовать движение тела в данный момент, недостаточно сказать, что оно движется со скоростью 50 км/ч, надо ещё указать направление его движения, т. е. направление скорости. В связи с этим указанные физические величины удобно изображать направленными отрезками. Такой способ изображения физических величин отличается наглядностью.
Направленный отрезок называется вектором .Термин «вектор» происходит от латинского слова «vector», что означает «несущий», «ведущий» или «переносящий».
Для
обозначения векторов пользуются
строчными латинскими буквами, над
которыми ставят стрелки: ![]()
![]() ,
,
![]() ,
... . Иногда вектор обозначают указанием
концов отрезка, изображающего вектор.
Например, вектор
,
... . Иногда вектор обозначают указанием
концов отрезка, изображающего вектор.
Например, вектор ![]() на рис. 5 можно обозначить
на рис. 5 можно обозначить ![]() (А – начало, В – конец вектора).
(А – начало, В – конец вектора).
Абсолютной
величиной
(или модулем) вектора называется длина
отрезка, изображающего вектор. Абсолютная
величина вектора
обозначается ![]() .
.
Направлением вектора называется направление, задаваемое лучом АВ.





Рис. 5 Рис. 6 Рис.7





Рис. 8
Вектор
называется нулевым,
если его начало совпадает с концом; ![]() ,
,
![]() - нулевые векторы.
- нулевые векторы.
Абсолютная
величина нулевого вектора равна нулю:
![]() = 0. Нулевой вектор не имеет определённого
направления.
= 0. Нулевой вектор не имеет определённого
направления.
Два нулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Векторы
,
,
коллинеарны ( рис. 6 ): ![]() ІІ
ІІ
.
При этом векторы
и
одинаково направлены , векторы
и
ІІ
ІІ
.
При этом векторы
и
одинаково направлены , векторы
и ![]() противоположно направлены.
противоположно направлены.
Нулевой вектор считается коллинеарным любому вектору.
Единичным
вектором
(или ортом)
называется вектор единичной длины. Орт
вектора
обозначается
0;
таким образом, ![]() = 1.
= 1.
Два вектора называются равными, если они совмещаются параллельным переносом (рис. 7).
Равные
векторы одинаково направлены и равны
по абсолютной величине; обратно: если
векторы одинаково направлены и равны
по абсолютной величине, то они равны.
Если
=
,
то
и
одинаково направлены и ![]() =
= ![]() ;
обратно; если
;
обратно; если ![]() и
одинаково направлены и
и
одинаково направлены и ![]() =
,
то
=
.
=
,
то
=
.
Координаты
вектора. Из
школьного курса математики известно,
что прямоугольная система координат
на плоскости определяется заданием
прямоугольного базиса ( ![]() ,
,
![]() ) и точки О ( рис. 8);
) и точки О ( рис. 8); ![]() – единичный
вектор оси абсцисс (Ox);
- единичный вектор оси ординат (Oy);
О – начало координат.
– единичный
вектор оси абсцисс (Ox);
- единичный вектор оси ординат (Oy);
О – начало координат.
Справедлива
теорема:
любой вектор
плоскости
можно разложить единственным образом
по
базисным векторам,
т. е.
= ![]() +
+ ![]() .
Коэффициенты x
и y
этого разложения называются координатами
вектора
в данной системе координат. Вектор
с координатами x
и y
записывают так:
(x,
y).
.
Коэффициенты x
и y
этого разложения называются координатами
вектора
в данной системе координат. Вектор
с координатами x
и y
записывают так:
(x,
y).
Координаты
точки А
(рис. 8) совпадают с соответствующими
координатами вектора ![]() .
Точку А с координатами x
и y
записывают так: А ( x,
y).
.
Точку А с координатами x
и y
записывают так: А ( x,
y).
Если точка лежит на оси абсцисс, то её ордината равна нулю: B (x, O); если же точка лежит на оси ординат, то её абсцисса равна нулю: C (0, y).
Расстояние
от точки A
(x,
y)
до оси абсцисс равно ![]() ,
а до оси ординат равно
,
а до оси ординат равно ![]() .
.
Абсолютная величина вектора равна квадратному корню из суммы квадратов его координат (рис. 8):
![]() .
.
Например,
абсолютная величина вектора ![]() ( - 5, 12) равна 13, так как
( - 5, 12) равна 13, так как ![]() .
.
Если
вектор задан двумя точками A
(xA,
yA)
и B
(xb,
yb),
то координаты вектора равны разностям
одноимённых координат конца и начала
вектора: ![]() (xb
– xA,
yb
–
ya).
(xb
– xA,
yb
–
ya).
Имеет место теорема: если векторы равны, то их соответствующие координаты равны также. Обратно: если соответствующие координаты векторов равны, то и сами векторы равны.
Пример
1.
Вычислить абсолютную величину вектора
![]() ,
если А ( - 2, 5), К (4, - 3).
,
если А ( - 2, 5), К (4, - 3).







Рис.10
 Рис.
9
Рис.
9
Решение. Сначала найдём координаты вектора: (4 – ( - 2), - 3 – 5), (6; - 8). Затем находим его абсолютную величину:
![]()
Сложение
векторов.
Суммой
векторов
![]() и
(x2,
y2)
называется вектор
(x1
+ x2,
y1
+ y2),
т. е.
и
(x2,
y2)
называется вектор
(x1
+ x2,
y1
+ y2),
т. е.
![]() (x1,
y1)
+
(x1,
y1)
+ ![]() (x2,
y2)
=
(x2,
y2)
= ![]() (x1
+ x2,
y1
+ y2).
(x1
+ x2,
y1
+ y2).
Справедлива
теорема: каковы бы ни были точки А, В, С,
имеет
место векторное равенство
![]() (рис. 9).
(рис. 9).
Векторное равенство называют правилом треугольника сложения векторов.
Сумма векторов и (рис. 10) найдена по правилу параллелограмма.
Вектором,
противоположным
вектору
,
называется вектор ![]() .
По определению, вектор, противоположный
нулевому вектору, есть нулевой вектор.
.
По определению, вектор, противоположный
нулевому вектору, есть нулевой вектор.
Сумма
двух противоположных векторов равна
нулю: ![]()
Разность
векторов
и
(обозначается ![]() )
называется сумма вектора
и вектора ( -
), противоположного
:
)
называется сумма вектора
и вектора ( -
), противоположного
:
![]() .
.
Если
векторы
и
отложены от одной точки О (рис. 11), то для
нахождения разности удобно пользоваться
таким правилом : ![]() .
.
Умножение вектора на число. Произведением вектора на число λ называется вектор λ (λx1, λy1), т. е.
λ∙![]() (x1,
y1)
= λ
(λx1,
λy1).
(x1,
y1)
= λ
(λx1,
λy1).
Справедлива
теорема: абсолютная
величина вектора ![]() равна произведению
равна произведению
![]() .
.






Рис. 11 Рис. 12
Направление
вектора
при ![]() совпадает с направлением вектора
,
если λ
совпадает с направлением вектора
,
если λ![]() 0,
и противоположно направлению вектора
,
если λ
0,
и противоположно направлению вектора
,
если λ![]() 0.
0.
На
рис. 12 изображены векторы
,
![]() ,
CD
= - 3
.
,
CD
= - 3
.
Произведением нулевого вектора на любое число и произведением любого вектора на нуль называется нулевой вектор.
Справедлива
теорема: для
того чтобы вектор
был коллинеарен ненулевому вектору
,
необходимо
и достаточно, чтобы существовало число
λ, удовлетворяющее условию ![]() .
Иными словами, соответствующие координаты
коллинеарных векторов пропорциональны.
Обратно: если соответствующие координаты
двух векторов пропорциональны, то
векторы коллинеарны.
.
Иными словами, соответствующие координаты
коллинеарных векторов пропорциональны.
Обратно: если соответствующие координаты
двух векторов пропорциональны, то
векторы коллинеарны.
Например,
векторы ![]() и
и ![]() коллинеарны, так как 10 = ( - 2)∙( - 5) и – 4 =
( - 2)∙2; кроме того, эти векторы противоположно
направлены, поскольку
коллинеарны, так как 10 = ( - 2)∙( - 5) и – 4 =
( - 2)∙2; кроме того, эти векторы противоположно
направлены, поскольку ![]() .
.
Пример
2. Даны
векторы ![]() ,
,
![]() .
Вычислить абсолютную величину вектора
.
Вычислить абсолютную величину вектора
![]() .
.
Решение.
Сначала найдём координаты векторов ![]() и -3
,
а затем сложим эти векторы:
и -3
,
а затем сложим эти векторы:



Рис. 13

![]()
![]()
Найдём
абсолютную величину вектора ![]() :
:
![]() .
.
Скалярное
произведение векторов.
Скалярным произведением векторов
(x1,
y1)
и
(x2,
y2)
называется число x1x2
+ y1y2
(равное сумме попарных произведений
соответствующих координат векторов).
Для скалярного произведения векторов
используется такая же запись, как и для
произведения чисел: ![]() .
.
Скалярное
произведение ![]() обозначается
обозначается ![]() и называется скалярным
квадратом.
Очевидно,
и называется скалярным
квадратом.
Очевидно, ![]()
![]() 2
.
2
.
Найдём,
например, скалярное произведение
векторов ![]() и
и ![]() :
:
![]() .
.
Углом
между
ненулевыми
векторами ![]() и
и ![]() называется угол ВАС (рис. 13). Углом между
любыми двумя векторами
и
называется угол между равными им
векторами с общим началом. Угол между
одинаково направленными векторами
считается равным нулю.
называется угол ВАС (рис. 13). Углом между
любыми двумя векторами
и
называется угол между равными им
векторами с общим началом. Угол между
одинаково направленными векторами
считается равным нулю.
Справедлива теорема: скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними:
![]() .
.
Из этой теоремы следует, что если векторы перпендикулярны, то их скалярное произведение равно нулю. Обратно: если скалярное произведение отличных от нуля векторов равно нулю, то векторы перпендикулярны.
Например,
векторы ![]() и
и ![]() перпендикулярны, так как
перпендикулярны, так как
![]()
![]() .
.
Вычислите
угла между двумя векторами.
Согласно предыдущей теореме, имеем
![]() cos
,
где
- величина угла между векторами
и
.
Отсюда
cos
,
где
- величина угла между векторами
и
.
Отсюда
Cos
= ![]() (где
,
(где
,
![]() ),
),
или в координатах
cos
=  .
.
Пример
3.
Вычислить угол между векторами ![]() и
и ![]() .
.
Решение. Для вычисления угла между векторами и воспользуемся приведённой формулой, но сначала найдём скалярное произведение векторов, абсолютные величины и произведение абсолютных величин векторов:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тогда
cos
![]() , т.
е.
, т.
е.
![]() .
.
Расстояние между двумя точками. В прямоугольной системе координат расстояние между двумя точками A (x1, y1) и B (x2, y2) вычисляется по формуле
![]() .
.
Это вытекает из того, что расстояние между двумя точками А и В равно абсолютной величине вектора , которая равна квадратному корню из суммы квадратов координат вектора, а вектор имеет координаты (x2 – x1, y2 – y1) (из координат конца вектора вычитаются одноимённые координаты начала вектора).
Пример 4. Вычислить расстояние между точками М и К, если и М ( - 5, 7) и К (7, - 9).
Решение.
Найдём
координаты вектора: ![]() (7 – ( - 5), - 9 – 7),
(12, - 16). Теперь найдём его длину:
(7 – ( - 5), - 9 – 7),
(12, - 16). Теперь найдём его длину: ![]() .
.





Рис. 14 Рис. 15
Деление отрезка в данном отношении. Если точка М делит отрезок между точками А (x1, y1) и В (x2, y2) в отношении АМ : МВ = λ (рис. 14), то координаты точки деления М находятся по формулам
X
= ![]() ,
y =
,
y = ![]() .
.
Если точка М делит отрезок АВ пополам, то λ = 1 и координаты точки М находятся по формулам
X
= ![]() ,
y
=
,
y
= ![]() ,
,
т. е. каждая координата середины отрезка равна полусумме одноимённых координат начала и конца отрезка.
Пример 5. Даны точки В ( - 1, 3) и С (8, - 12). Найти координаты точек М и N, которые делят отрезок на три равные части (рис. 15).
Решение.
Точка N
делит отрезок ВС в отношении λ
= ![]() ,
тогда xN
=
,
тогда xN
= ![]() ,
yN
=
,
yN
= ![]() .
.
Подставляем в эти формулы координаты точек В и С:
XN
= ![]() ,
,
YN
= ![]() ,
т. е. N
(5 – 7).
,
т. е. N
(5 – 7).
Точка М делит отрезок BN пополам; значит,
XM
= ![]() ,
yM
=
,
yM
= ![]() .
.
или
xM
= ![]() ,
yM
=
,
yM
= ![]() ,
,
т. е. М (2, - 2).
Пример
6.
Даны векторы ![]() (3, - 2) и
(5, 1). Вычислить скалярное произведение
(5
(3, - 2) и
(5, 1). Вычислить скалярное произведение
(5![]() )
∙ 5
.
)
∙ 5
.
Решение.
Сначала найдём координаты векторов
5![]() и 5
:
и 5
:

![]()
5![]()
Скалярное произведение векторов равно сумме попарных произведений соответствующих координат векторов:
(5
)
5![]()
Пример 7. Доказать, что треугольник с вершинами A (2, 2), B ( - 1, 6) и С ( - 5, 3) – прямоугольный.
Решение. Сначала найдём длину каждой стороны треугольника АВС:
![]()
![]()
![]() ;
;
![]()
Теперь воспользуемся теоремой, обратной теореме Пифагора: если в треугольнике сумма квадратов двух сторон равна квадрату большей стороны, то этот треугольник прямоугольный и против большей стороны лежит прямой угол.
Так
как ![]() то треугольник АВС – прямоугольный и
величина угла АВС равна 900.
то треугольник АВС – прямоугольный и
величина угла АВС равна 900.
Пример 8. Найти на оси Oy точку М, отстоящую от точки K (3, 7) на 5 единиц.
Решение.
Так как точка M
лежит на оси Оy,
то её абсцисса равна 0: M
(0, y).
Остаётся найти её ординату из условия
![]() Имеем
Имеем ![]() По условию,
По условию, ![]() откуда 9 + (y
– 7)2
= 25, (y
– 7)2
= 16, y
– 7 = ± 4, y1
= 11, y2
= 3. Итак, задача имеет два решения: М1
(0, 3) и М2
(0, 11).
откуда 9 + (y
– 7)2
= 25, (y
– 7)2
= 16, y
– 7 = ± 4, y1
= 11, y2
= 3. Итак, задача имеет два решения: М1
(0, 3) и М2
(0, 11).
П
 ример
9.
Даны три вершины A
( - 1, 2), B
(4, 3), C
(7, 5) параллелограмма ABCD.
Вычислить координаты вершины D.
ример
9.
Даны три вершины A
( - 1, 2), B
(4, 3), C
(7, 5) параллелограмма ABCD.
Вычислить координаты вершины D.





Рис. 16 Рис. 17
Решение. Диагонали параллелограмма ABCD (рис. 16) точкой М делятся пополам, т. е. точка М – середина отрезков AC и BD. Имеем xМ(xA + xC)/2, yM = m(yA +yC)/2, или xM = ( - 1+7)/2 = 6/2 = 3, yM = (2+5)/2 = 7/2 = 3,5. Итак, М (3, 3,5).
Далее, xM = (xB = xD)/2, откуда xD = 2xM - xB, xD = 2∙3 – 4 = 2; yM = (yB + yD)/2, откуда yD = 2yM - yB, yD = 2∙3, 5 – 3 = 4. Итак, D (2, 4).
Пример 10. Найти центр тяжести треугольной однородной пластинки, вершинами которой служат точки A (1, 4), B ( - 5, 0) и C ( - 2, - 1).
Решение. Из физики известно, что искомая точка М есть точка пересечения медиан треугольника, которая делит каждую медиану в отношении 2 : 1, считая от вершины треугольника (рис. 17).
Точка K – середина стороны АВ. Тогда xK = (xA = xB)/2, xK = (1 – 5)/2 = - 2, yK = (yA + yB)/2, yK = (4 + 0)/2 = 2.
Итак, K ( - 2, 2).
Точка М делит отрезок CK в отношении λ = 2/1 = 2. Тогда
xM
= ![]() xM
=
xM
= ![]()
yM
= ![]() ,
yM
=
,
yM
= ![]()
Итак, М ( - 2, 1).
У РАВНЕНИЕ
ЛИНИИ НА ПЛОСКОСТИ.
РАВНЕНИЕ
ЛИНИИ НА ПЛОСКОСТИ.
По данной теме сначала изучите § 28 – 41 гл. 2 [4] или § 1 – 10 гл. 2, § 1, 2 гл. 3 [7]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из этого пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [4], гл. 2, № 7, 13 – 18, 25, 39 – 43, 44 (1 – 3), 51, 54, 66 – 68, или [7], гл. 2, № 14 – 51.
Понятие об уравнении линии на плоскости.
Пусть
на плоскости задана прямоугольная
система координат xOy
(рис. 18). Рассмотрим в этой системе
координат некоторую линию ![]() .
.
Уравнением данной линии (в выбранной на плоскости системе координат) называется такое уравнение с переменными x и y, которому удовлетворяют координаты каждой точки, лежащей на этой линии, и не удовлетворяют координаты каждой точки, не лежащей на ней.
В общем виде уравнение линии в прямоугольных координатах записывается так: F (x, y) = 0.
Если известно уравнение некоторой линии, то для любой точки плоскости можно установить, лежит ли точка на этой линии или нет. Для этого достаточно подставить в данное уравнение вместо переменных x и y координаты точки; если при этом получается верное числовое равенство, то точка лежит на линии; если равенство окажется неверным, то точка не лежит на линии.
Например, точка A ( - 2, 2) лежит на линии x2 – 2y = 0, так как ( - 2)2 – 2 ∙ 2 = 0; точка В (2, - 3) не лежит на линии x3 – y2 = 3, поскольку 23 – ( - 3)2≠3.
Прямая на плоскости и её уравнения. Прямые – самые простые линии на плоскости. Им соответствуют и самые простые уравнения. Имеет место теорема: всякая прямая на плоскости определяется уравнением первой степени с двумя переменными x и y: всякое уравнение вида Ax + By + C = 0 при любых действительных значениях коэффициентов А, В и С, исключая одновременное равенство нулю коэффициентов А и В, определяет прямую.
Уравнение Ax + By + C = 0 называется общим уравнением прямой. Его частные случаи:
X = 0 – уравнение оси координат Oy;
Y = 0 – уравнение оси абсцисс Ox;
X = a – уравнение прямой, проходящей через точку А (a, 0) параллельно оси ординат (рис.19);
Y = b – уравнение прямой, проходящей через точку В (0, b) параллельно оси абсцисс (рис.20).





Рис. 19 Рис. 20


Рис. 21
Положение прямой на плоскости относительно системы координат можно задать различными способами. Например, прямая однозначно определяется: двумя различными точками; точкой и направлением; отрезками, отсекаемыми прямой на осях координат, и т. д. Однако, обязательно должна быть дана точка, лежащая на этой прямой.
Пусть точка М1 (x1, y1) лежит на прямой 𝒍 (рис. 21): M1 (x1, y1) 𝒍. Для составления уравнения прямой 𝒍 можно использовать следующую схему:
взять на прямой 𝒍 произвольную точку с текущими координатами x, y : М (x, y) 𝒍 (рис. 21);
найти координаты вектора, лежащего на прямой 𝒍, начинающегося в данной точке М1 и оканчивающегося в точке M :
 (x
– x1,
y
- y1);
(x
– x1,
y
- y1);найти координаты известного вектора, параллельного ( или перпендикулярного) прямой;
воспользоваться условием коллинеарности (или перпендикулярности) векторов.
В зависимости от способа задания прямой рассматривают различные виды её уравнения.
Уравнение
прямой, проходящей через данную точку
М1
(x1,
y1),
с заданным нормальным вектором ![]() (
А, В) (рис. 22):
(
А, В) (рис. 22):
A (x – x1) + B (y – y1) = 0.
Нормальным вектором прямой называется всякий ненулевой вектор, перпендикулярный этой прямой. Любая прямая имеет бесконечное множество нормальных векторов, которые коллинеарны между собой.










Рис. 22 Рис. 23
Рис. 24
Уравнение прямой, проходящей через данную точку M1 (x1, y1), с заданным направляющим вектором (m, n) (рис. 23):
![]()
Направляющим вектором прямой называется всякий ненулевой вектор, параллельный этой прямой. Любая прямая имеет бесконечное множество направляющих векторов, которые коллинеарны между собой.
Уравнение прямой с угловым коэффициентом (рис. 24):
y = kx + b.
Угловым коэффициентом прямой называется тангенс угла наклона прямой к положительному направлению оси абсцисс: k = tg (рис. 24).
Уравнение прямой в отрезках:
![]()
где a и b – длины отрезков, отсекаемых прямой 𝒍 на осях координат (рис. 25), взятые с соответствующими знаками (в зависимости от того, положительные или отрицательные полуоси координат пересекает прямая 𝒍).
Так,
уравнение прямой 𝒍1
(рис. 26) имеет вид ![]() или
3x
– 2y
– 6 = 0.
или
3x
– 2y
– 6 = 0.
Уравнение прямой, проходящей через две данные точки М1 (x1, y1) и M2 (x2, y2):
![]()
Если абсцисс точек М1 и М2 параллельна оси ординат и уравнение её имеет вид

 x
= a.
x
= a.




Рис. 25 Рис. 26
При равенстве ординат точек М1 и М2, т. е. при y1 = y2 = b, прямая М1М2 параллельна оси абсцисс и её уравнение таково:
y = b.
Общее уравнение прямой:
Ax + By + C = 0.
Его частные случаи:
если A ≠ 0, В ≠ 0, С = 0, то Ax + By = 0 – уравнение прямой, проходящей через начало координат;
если А ≠ 0, В = 0, С ≠ 0, то Ax + C = 0 – уравнение прямой, параллельно оси Ox;
если А ≠ 0, В = 0, С = 0, то Ax = 0 или x = 0 – уравнение оси Oy;
если А = 0, В ≠ 0, С ≠ 0, то By + C = 0 – уравнение прямой, параллельно оси Ox;
если А = 0, В ≠ 0, С = 0, то By = 0 или y = 0 – уравнение оси Ox.
Каждое из приведённых уравнений прямой можно получить, используя рассмотренную выше схему составления уравнения прямой.
Составим, например, уравнение прямой 𝒍, проходящей через две данные точки: M1 (x1, y1) и M2 (x2, y2) (рис. 27).
возьмём на прямой 𝒍 произвольную точку с текущими координатами x, y : M (x, y) 𝒍.
найдём координаты вектора, лежащего на прямой 𝒍 : (x – x1, y – y1).
найдём координаты известного вектора, параллельного прямой 𝒍 :
 (x2
– x1,
y2
–
y1).
(x2
– x1,
y2
–
y1).Так как
 ,
то соответствующие координаты этих
векторов пропорциональны:
,
то соответствующие координаты этих
векторов пропорциональны:
![]()




Рис. 27
Это и есть уравнение прямой 𝒍, проходящей через точки М1 и М2.
Действительно,
это уравнение с двумя переменными x
и y,
причём ему удовлетворяют координаты
точек, лежащих на прямой 𝒍,
и не удовлетворяют координаты точек,
не лежащих на этой прямой (так как если
K
![]() 𝒍,
то M1K
∦
𝒍,
то M1K
∦![]() и, следовательно, соответствующие
координаты этих векторов не пропорциональны).
и, следовательно, соответствующие
координаты этих векторов не пропорциональны).
Если прямая задана общим уравнением Ax + By + C = 0, то её нормальный вектор имеет координаты (A, B), а угловой коэффициент k = - A/B.
Так прямая 2x – 3y + 7 = 0 имеет нормальный вектор n (2, - 3) и угловой коэффициент k = 2/3.
Угол между двумя прямыми. Угол между двумя прямыми называется величина меньшего из углов, образованных этими прямыми (рис. 28).
Угол между двумя прямыми можно вычислять по формуле
cos
![]() или
cos
или
cos
![]()
где
![]() ,
,
![]() - нормальные векторы прямых 𝒍1
и 𝒍2,
а
- нормальные векторы прямых 𝒍1
и 𝒍2,
а ![]() ,
,
![]() - направляющие векторы этих прямых (рис.
28).
- направляющие векторы этих прямых (рис.
28).
Эта формула удобна для вычисления угла между прямыми, заданными их общими уравнениями.
Если прямые 𝒍1 и 𝒍2 не перпендикулярны, то угол между ними можно вычислить и по формуле
tg
![]()
где k1 и k2 – угловые коэффициенты прямых 𝒍1 и 𝒍2. Эта формула удобна для вычисления угла между прямыми, заданными их уравнениями с угловыми коэффициентами.






Рис. 28
Пример 1. Вычислить угол между прямыми x + 5y – 3 = 0 и 2x – 3y + 4 = 0.
Решение. Угол между данными прямыми найдём по формуле
cos
![]() где
где ![]() (1,
5),
(1,
5), ![]() (2, - 3).
(2, - 3).
Сначала найдём скалярное произведение нормальных векторов, их абсолютные величины и произведения абсолютных величин нормальных векторов:
![]()
![]()
![]()
Тогда
cos
![]() ;
;
![]() arccos
arccos
![]()
Итак, угол между данными прямыми равен 450.
Условие параллельности двух прямых. Пусть на плоскости заданы две прямые: A1x + B1 + C1 = 0 (𝒍1) и A2x + B2y + C2 = 0 (𝒍2). Если прямые параллельны (𝒍1‖𝒍2), то их нормальные векторы (A1, B1) и (A2, B2) коллинеарны (рис. 29), а это значит, что их соответствующие координаты пропорциональны: А1/A2 = B1/B2. Справедливы и обратное утверждение.
Итак, две прямые параллельны тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны (или когда их угловые коэффициенты равны между собой: k1 = k2).
Например, прямые 3x – y + 1 = 0 и 6x – 2y – 3 = 0 параллельны, так как 3/6 = ( - 1)/( - 2).
Условие
перпендикулярности двух прямых.
Если прямые перпендикулярны (𝒍1┴𝒍2),
то их нормальные векторы
(A1,
B1)
и
(A2,
B2)
также перпендикулярны (рис. 30), а это
значит, что их скалярное произведение
равно нулю: ![]() или A1A2
+ B1B2
= 0. Справедливо и обратное утверждение.
или A1A2
+ B1B2
= 0. Справедливо и обратное утверждение.








Рис. 29 Рис. 30
Итак, две прямые перпендикулярны тогда и только тогда, когда коэффициенты при переменных связаны равенством А1А2 + В1В2 = 0 (или когда их угловые коэффициенты обратны по модулю и противоположны по знаку: k1 = - 1/k2).
Например, прямые 3x + 2y – 1 = 0 и 6y – 4x + 7 = 0 перпендикулярны, так как 3 ∙ ( - 4) + 2 ∙ 6 = 0.
Точка пересечения двух прямых. Если прямые A1x + B1y + C1 = 0 и A2x + B2y + C2 = 0 не параллельны, то для нахождения точки их пересечения надо решить систему, составленную из уравнений этих прямых:
![]()
Решение системы (x1, y1) даёт координаты точки пересечения этих прямых.
Например, прямые x + 3y = 0 и 2x + 5y = - 1 пересекаются в точке ( - 3, 1), так как упорядоченная пара чисел x = - 3, y = 1, т. е. ( - 3, 1), является решением системы:
![]()
![]()
![]()
![]()
![]()
Построение прямой. Для построения прямой достаточно построить две её точки.
а) Для построения прямой Ax + By + C = 0, не проходящей через начало координат, достаточно найти точки её пересечения с осями координат:
Ox:
![]() Oy:
Oy: ![]()
б )
Для построения прямой Ax
+ By
= 0, проходящей через начало координат,
достаточно взять точки (0, 0) и (t,
- At/B),
где t
)
Для построения прямой Ax
+ By
= 0, проходящей через начало координат,
достаточно взять точки (0, 0) и (t,
- At/B),
где t![]() R.
R.







Рис.31 Рис.32
Пример 2. Построить прямую 2x – 3y – 9 = 0.
Решение. Данная прямая не проходит через начало координат, поэтому находим точки её пересечения с осями координат:
Ox:
![]() 2x – 9 = 0, 2x = 9, x = 4, 5;
2x – 9 = 0, 2x = 9, x = 4, 5;
Oy:
![]() - 3 – 9 = 0, -3y = 9, y = - 3.
- 3 – 9 = 0, -3y = 9, y = - 3.
Строим найденные точки и проводим через них прямую (рис. 31).
Пример 3. Построить прямую x + 2y = 0.
Решение. Данная прямая проходит через начало координат, поэтому строим точки (0, 0) и (2, - 1) и проводим через них прямую (рис. 32).
Пример 4. Даны вершины треугольника А ( - 2, 1), В (4, - 3), С ( - 3, 5). Составить уравнение: высоты, опущенной из вершины В на сторону АС; медианы, проведённой из вершины С (рис. 33). Сделать чертёж.
Решение. Воспользуемся схемой составления уравнения прямой. Сначала найдём уравнение высоты BK:
M (x, y) BK;
 (x – 4, y – ( - 3)),
(x – 4, y + 3);
(x – 4, y – ( - 3)),
(x – 4, y + 3); ( - 3 – ( - 2), 5 – 1),
( - 1, 4).
( - 3 – ( - 2), 5 – 1),
( - 1, 4). ┴
┴ 
 = 0, или - 1 (x
– 4) + 4 (y
+ 3) = 0, - x
+ 4 + 4y
+ 12 = 0,
= 0, или - 1 (x
– 4) + 4 (y
+ 3) = 0, - x
+ 4 + 4y
+ 12 = 0,
X – 4y – 16 = 0 – уравнение высоты BK.








Рис. 33
Чтобы составить уравнение медианы CP, надо найти координаты точки P, которая является серединой отрезка АВ. Значит, Xp = (XA + XB)/2, Yp = (yA + yB)/2, т. е. Xp = ( - 2 + 4)/2 = 2/2 = 1, yP = (1 – 3)/2 = - 2/2 = - 1. Итак, P (1, - 1).
Теперь найдём уравнение медианы CP:
N (x, y) CP;
 (x – ( - 3), y – 5),
(x + 3, y – 5);
(x – ( - 3), y – 5),
(x + 3, y – 5); (1 + 3, - 1 – 5),
(1 + 3, - 1 – 5),  (4, - 6);
(4, - 6);
 (2, - 3);
(2, - 3); ‖
⇒
‖
⇒ ,
,
3x + 9 = -2y + 10, 3x + 9 + 2y – 10 = 0,
3x + 2y – 1 = 0 – уравнение медианы CP.
Сделаем чертёж в системе координат (рис. 34).
Пример 5. Из точки А (3, -2) на прямую 2x + y + 1 = 0 опущен перпендикуляр. Составить его уравнение (рис. 35). Сделать чертёж.
Решение.
M (x, y) AB;
 (x – 3, y + 2);
(x – 3, y + 2); (2, 1);
(2, 1);‖
 ⇒
⇒ ,
x – 3 = 2y + 4,
,
x – 3 = 2y + 4,
x – 2y – 7 = 0 – уравнение перпендикуляра, опущенного из точки А на прямую 2x + y + 1 = 0.
Сделаем чертёж в системе координат (рис. 36). Прямые 2x + y + 1 = 0 и x – 2y – 7 = 0 построим по точкам их пересечения с осями координат:
2x + y + 1 = 0, Ox:
 Oy:
Oy: 
x – 2y – 7 = 0, Ox:
 Oy:
Oy: 
Пример 6.вычислить угол между прямыми 6x – 2y + 9 = 0 и 4x + 2y – 7 = 0. Сделать чертёж.

















Рис. 34 Рис.35
Решение. Угол между данными прямыми найдём по формуле
cos
= ![]() ,
где
,
где ![]() (6,
- 2),
(4,
2).
(6,
- 2),
(4,
2).
Сначала найдём скалярное произведение нормальных векторов, их абсолютные величины и произведение абсолютных величин нормальных векторов:
![]() = 6 ∙ 4 + ( - 2) ∙ 2 = 24 – 4 = 20,
= 6 ∙ 4 + ( - 2) ∙ 2 = 24 – 4 = 20,
![]()
![]()
![]()
Тогда
cos
=
![]() = arcos
= arcos
![]()
Итак, угол между данными прямыми равен 450.
Сделаем чертёж в системе координат (рис.37). данные прямые построим по точкам их пересечения с осями координат:
6x – 2y + 9 = 0, Ox:
 Oy:
Oy: 
4x + 2y – 7 = 0, Ox:
 Oy:
Oy: 
Пример 7. Две стороны квадрата определяются уравнением x + 3y + 10 = 0 и 3x – y – 20 = 0, а его центр лежит в точке М (3, - 1). Составить уравнение диагоналей квадрата (рис. 38).









Рис. 36 Рис. 37







Рис. 38
Решение. В условии даны уравнения двух смежных сторон квадрата, так как прямые x + 3y + 10 = 0 и 3x – y – 20 = 0 перпендикулярны (1 ∙ 3 + 3 ( - 1) = 0). Пусть это уравнения сторон АВ и АD.
С начала
найдём координаты точки А, которая
является точкой пересечения данных
прямых:
начала
найдём координаты точки А, которая
является точкой пересечения данных
прямых:
![]() 3
3
![]()
![]()
![]()
![]()
![]()
![]()
Итак, А (5, - 5).
Теперь найдём уравнение диагонали АС:
K (x, y) AC;

 (3 – 5, - 1 + 5),
( - 2, 4),
( - 1, 2);
(3 – 5, - 1 + 5),
( - 2, 4),
( - 1, 2); ‖
⇒
‖
⇒

2x – 10 = - y – 5, 2x – 10 + y + 5 = 0.
2x + y – 5 = 0 – уравнение диагонали АС.
По этой же схеме найдём уравнение диагонали BD:









Рис. 39
Рис. 40
P (x, y) BD;
 (x – 3, y + 1);
(x – 3, y + 1);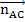 (2, 1);
(2, 1);‖
 ⇒
⇒
 x – 3 = 2y + 2,
x – 3 = 2y + 2,
X – 2y – 5 = 0 – уравнение диагонали BD.
Пример 8. Найти проекцию точки P ( - 6, 4) на прямую 4x – 5y + 3 = 0 (рис. 39). Сделать чертёж.
Решение. Начала найдём уравнение прямой 𝒍1:
M (x, y) 𝒍1;
 (x + 6, y – 4);
(x + 6, y – 4);(4, - 5);
‖ ⇒
 5x + 30 = - 4y + 16,
5x + 30 = - 4y + 16,
5x + 4y + 14 = 0 – уравнение прямой 𝒍1.
Теперь найдём точку пересечения прямых 𝒍 и 𝒍1, для чего решим систему уравнений:

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Итак, K ( - 2, - 1) – проекция точки P ( - 6, 4) на прямую 4x – 5y + 3 = 0.
Сделаем чертёж в системе координат (рис. 40). Прямую 4x – 5y + 3 = 0 построим по точкам её пересечения с осями координат:
Ox:
![]() Oy:
Oy:
![]()
ПРОИЗВОДНАЯ И ЕЁ ПРИЛОЖЕНИЯ.
По данной теме сначала изучите § 27 – 30 гл. 6 [2] или § 1 – 7 гл. 5 [7].
Производная. Понятие производной является одним из фундаментальных понятий математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.
Пусть функция y = f (x) определена в промежутке X. возьмём из этого промежутка фиксированное значение аргумента x и придадим ему приращения x так, чтобы новое значение аргумента x + x принадлежало этому промежутку. Тогда значение функции f (x) заменится новым значением f (x) + y = f (x + x) т. е. функция получит приращение y = f (x + x) – f (x).
Предел отношения приращения функции y к вызвавшему его приращению аргумента x при стремлении x к нулю, т. е.
![]()
называется производной функции y = f(x) по аргументу x в точке x.
П роизводная
обозначается одним из символов: y’x,
y’,
f’
(x),
роизводная
обозначается одним из символов: y’x,
y’,
f’
(x),
![]() ,
а
её значение при x
= x0
обозначается y’
(
x0),
y’
(x0),
f’
(x0),
x
= x0.
,
а
её значение при x
= x0
обозначается y’
(
x0),
y’
(x0),
f’
(x0),
x
= x0.
Операция нахождения производной называется дифференцированием.
Если функция f (x) имеет производную в точке x, то она называется дифференцируемой в этой точке.
Если функция f (x) имеет производную в каждой точке промежутка X, то говорят, что эта функция дифференцируемая на этом промежутке.
Производная сложной функции. Пусть y = f (u), где и является не независимой переменной, а функцией независимой переменной x: u = (x). таким образом, y = f ( (x)).
В этом случае функция y называется сложной функцией x, а переменная u – промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы: если y = f (u) и u = (x) – дифференцируемые функции своих аргументов, то производная сложной функции y = f ( (x)) существует и равна произведению производной функции y по промежуточному аргументу u на производную промежуточного аргумента и по независимой переменной x:
y’x = y’uu’x.
Эта теорема распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Например,
если y
= f
(u),
u
=
(![]() ),
=
),
= ![]() (x),
т. е. y
= f
(
(𝝍
(x))),
то y’x
= y’u
(x),
т. е. y
= f
(
(𝝍
(x))),
то y’x
= y’u![]()
![]() ’x.
’x.
Формулы дифференцирования. Во всех приведённых ниже формулах буквами u и обозначены дифференцируемые функции независимой переменной x: u = u (x), = (x), а буквами a, c, n – постоянные:
c’ = 0.
x’ = 1.
(u
 )’
= u’
)’
= u’ .
.(u )’ = u
 .
.(cu)’ = cu’.
(

Остальные формулы записаны как для функций независимой переменной, так и для сложных функций:
(xn)’ = nxn – 1. 7a. (un)’ = nun – 1 u’.
(
 8a.
(
8a.
( )’
= -
)’
= -  .
.(
 9a.
(
9a.
( )’
=
)’
=  .
.(sin x)’ = cos x. 10a. (sin u)’ = cos u ∙ u’.
(cosx)’ = - sin x. 11a. (cos u)’ = - sin u ∙ u’.
(tg x)’ =
 12a.
(tg
u)’ =
12a.
(tg
u)’ =  .
.(ctg x)’ = -
 .
13a.
(ctg
u)’
= -
.
13a.
(ctg
u)’
= -  .
.(ax)’ = axln a. 14a. (au)’ = an ln a ∙ u’
(cx)’ = ex. 15a. (eu)’ = eu u’.
(ln
 )’
=
)’
=  .
16a.
(ln
.
16a.
(ln
 ’
=
’
=  .
.(loga )’ =
 .
17a.
(loga
)’
=
.
17a.
(loga
)’
=  ,
,
где
a
0,
а ![]() 1.
1.
При решении приведённых ниже примеров сделаны подробные записи. Однако следует научиться дифференцировать без промежуточных записей.
Пример
1.
Найти производную функции y
= 5x3
– 2x
+ ![]() .
.
Решение. Данная функция есть алгебраическая сумма функций. Дифференцируем её, используя формулы 3, 5, 7 и 8:
y’
= (5x3)’
– (2x)’ + (
![]() )’
= 5(x3)’
– 2x’ -
)’
= 5(x3)’
– 2x’ -
![]() = 5
∙ 3x2
– 2 -
= 15x2
– 2 -
.
= 5
∙ 3x2
– 2 -
= 15x2
– 2 -
.
Пример
2. Найти
производную функцию f
(x
) = ![]()
Решение.
Применяя
формулы 6, 3, 7 и 1, получим f’
(x)
= ![]() =
= ![]()
Пример 3. Найти производную функции y = sin3 и вычислить её значение при = /3.
Решение. Это сложная функция с промежуточным аргументом sin . Используя формулы 7а и 10, имеем
f’ ( ) = 3 sin2 (sin )’ = 3 sin2 cos .
Вычислим значение производной при = /3:
f’
( ![]() ) = 3 sin2
cos
) = 3 sin2
cos ![]()
Пример
4.
Найти производную функции y
= ![]()
Решение. Это сложная функции с промежуточным аргументом cos x. Применяя формулы 3, 5, 7а, 11, 16а, получим
y’
= (![]() )’
– (ln cos x)’ =
)’
– (ln cos x)’ = ![]() = =
= =![]() =
= ![]() =
= ![]() = tg x sin2x.
= tg x sin2x.
Пример
5.
Найти производную функции y
= ![]()
Решение. Дифференцируем данную функцию по формулам 6, 12, 3 3 и 1:
y’
= ![]()
![]() =
= ![]() =
=
![]() =
= ![]() =
= ![]()
Пример
6.
Найти производную функции s
= ln
![]() и
вычислить её значение при t
= 2.
и
вычислить её значение при t
= 2.
Решение. Сначала преобразуем функцию, используя свойства логарифмов:
S
= ln
t
-
ln
(1 + ![]() ).
).
Теперь дифференцируем по формулам 3, 16a, 7 и 1:
s’
= (ln t)’ – (
ln (1 + ![]() )
)’ =
)
)’ = ![]() =
= ![]() -
- ![]() =
= ![]()
Вычислим значение производной при t = 2:
s’
(2) = ![]()
Пример
7. Найти
производную функции y
= ![]() и
вычислить её значение при x
= 0.
и
вычислить её значение при x
= 0.
Решение. Используем формулы 6, 3, 14a, 9a, 5 и 1:

Вычислим значение производной при x = 0:
y’
(0) = ![]()
Геометрический смысл производной. Производная функции имеет простую и важную геометрическую интерпретацию.
Если функция y = f (x) дифференцируема в точке x, то график этой функции имеет в соответствующей точке касательную, причём угловой коэффициент касательной равен значению производной в рассматриваемой точке.
Угловой коэффициент касательной, проведённый к графику функции y = f (x) в точке (x0, y0), равен значению производной функции при x = x0, т. е. kкас = y’ (x0).
Уравнение этой касательной имеет вид
y = y0 = f’ (x0) (x – x0).
Пример
8.
Составить уравнение касательной к
графику функции y
= ![]() x3
– x2
– 2x
+ 3 в точке А (3, 6).
x3
– x2
– 2x
+ 3 в точке А (3, 6).
Решение. Для нахождения углового коэффициента касательной найдём производную данной функции:
y’ = - 3x2 – 2x – 2 = 2x2 – 2x – 2.
Угловой коэффициент касательной равен значению производной функции при x = 3:
k = y’ (3) = 2 ∙ 32 – 2 ∙ 3 – 2 = 18 – 6 – 2 = 10.
Уравнение касательной имеет вид
y – 6 = 10 (x – 3), или y – 6 = 10x – 30, т. е. 10x – y – 24 = 0.
Пример
9.
Составить уравнение касательной,
проведённой к графику функции y
= ![]() в точке с абсциссой x
= 2.
в точке с абсциссой x
= 2.
Решение. Сначала найдём ординату точки касания A (2, y). Так как точка А лежит на кривой, то её координаты удовлетворяют уравнению кривой, т. е.
y
= ![]() ;
А (2, 2).
;
А (2, 2).
Уравнение касательной, проведённой к кривой в точке А (2, 2), имеет вид y – 2 = k (x – 2). Для нахождения углового коэффициента касательной найдём производную:
y’
= ![]()
Угловой коэффициент касательной равен значению производной функции при x = 2:
k
= y’
(2) = - ![]()
Уравнение касательной таково:
Y – 2 = - (x – 2), y – 2 = - x + 2, т. е. x + y – 4 = 0.
Физический
смысл производной.
Если тело движется по прямой по закону
s
= s
(t),
то за промежуток времени
t
(от момента t
до момента t
+
t)
оно пройдёт некоторый путь
s.
Тогда ![]() есть
средняя скорость движения за промежуток
времени
t.
есть
средняя скорость движения за промежуток
времени
t.
Скоростью движения тела в данный момент времени t называется предел отношения приращения пути s к приращению времени t, когда приращение времени стремится
(t) = ![]() =
=
![]() .
.
Следовательно, производная пути s по времени t равна скорости прямолинейного движения тела в данный момент времени:
(t ) = s’t .
Скорость протекания физических, химических и других процессов также выражается с помощью производной.
Производная функции y = f (x) равна скорости изменения этой функции при данном значении аргумента x:
(x) = y’ = ![]()
Пример 10. Закон движения точки по прямой задан формулой s = 5t3 – 3t2 + 4 (s – в метрах, t – в секундах). Найти скорость движения точки в конце первой секунды.
Решение. Скорость движения точки в данный момент времени равна производной пути s по времени t:
![]() (t)
= s’
= 15t2
– 6t,
(1) = 15 – 6 = 9.
(t)
= s’
= 15t2
– 6t,
(1) = 15 – 6 = 9.
Итак, скорость движения точки в конце первой секунды равна 9 м/c.
Пример 11. Тело, брошенное вертикально вверх, движется по закону s = 0t - gt2, где 0 – начальная скорость, g – ускорение свободного падения тела. Найти скорость этого движения для любого момента времени t. Сколько времени будет подниматься тело и на какую высоту оно поднимается, если 0 = 40 м/с?
Решение. Скорость движения точки в данный момент времени t равна производной пути s по времени t:
(t) = s’ = 0 - g ∙ 2t = 0 – gt.
В высшей точке подъёма скорость тела равна нулю:
0
– gt = 0, gt =
0,
t =
0/g,
t = 40/g![]() 4, 1 t = 4, 1.
4, 1 t = 4, 1.
За 40/g секунд тело поднимается на высоту
s
= 40 ![]()
Вторая производная. Производная функции y = f (x) в общем случае является функцией от x. Если от этой функции вычислить производную, то получим производную второго порядка или вторую производную функции y = f (x).
Второй производной функции y = f (x) называется производная от её первой производной y’ = f’ (x).
Вторая
производная функции обозначается одним
из символов - y”,
f”
(x),
![]() .
Таким образом, (y’)’
= y”.
.
Таким образом, (y’)’
= y”.
Аналогично определяются и обозначаются производные любого порядка. Например, производная третьего порядка:
(y”)’
= y”’
или f”’
(x),
![]()
Пример 12. Найти вторую производную функции f (x) = esinx.
Решение. Сначала найдём первую производную
f’ (x) = esin x (sin x)’ = esin x cos x.
Дифференцируя ещё раз, найдём вторую производную:
f” (x) = esin x (cos x)’ + (esin x)’ cos x = esin x ( - sin x) + esin x cos x ∙ cos x = = esin x (cos2x – sin x).
Пример
13. Найти
вторую производную функции y
= ![]() и
вычислить её значение при x
= 2.
и
вычислить её значение при x
= 2.
Решение. Сначала найдём первую производную:
y’
= ![]()
Дифференцируя ещё раз, найдём вторую производную:

Вычислим значение второй производной при x = 2; имеем y” (2) = 4/(2-1)3 = 4/1 = 4.
Физический смысл второй производной. Если тело движется прямолинейно по закону s = s (t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t:
A (t) = ’ = s”.
Таким образом, первая производная характеризует скорость некоторого процесса, а вторая производная – ускорение того же процесса.
Пример 14. Точка движется по прямой по закону s = t – sin t. Найти скорость и ускорение движения при t = /2.
Решение .Скорость движения тела в данный момент времени равна производной пути s по времени t, а ускорение – второй производной пути s по времени t.
Находим:
(t) = s’ = 1 – cos t; тогда
(![]() )
= 1 – cos
)
= 1 – cos ![]() = 1;
= 1;
a (t) = s” = - ( - sin t) = sin t; тогда a ( ) = sin = 1.
Пример 15. Скорость прямолинейного движения пропорциональна квадратному корню из пройденного пути (как, например, при свободном падении). Доказать, что это движение происходит под действием постоянной силы.
Решение. По закону Ньютона, сила F, вызывающая движение, пропорциональна ускорению, т. е.
F = Ka (t) или F = Ks” (t).
Согласно
условию,
(t)
= s’
(t)
= ![]()
![]() .
Дифференцируя это равенство, найдём
.
Дифференцируя это равенство, найдём
a
(t)
= s”
(t)
= ![]() s’
(t)
=
λ
=
s’
(t)
=
λ
= ![]() .
.
Следовательно, действующая сила F = Kλ2/2 = const.
Приложения производной к исследованию функций.
Условие постоянства функции. Дифференцируемая функция y = f (x) постоянна на промежутке X тогда и только тогда, когда f’ (x) = 0 внутри X.











Рис. 41 Рис. 42
Условие
возрастания функции.
Дифференцируемая функция y
= f
(x)
монотонно возрастает на промежутке X
тогда и только тогда, когда её производная
не отрицательна внутри этого промежутка:
f’
(x)
![]() 0, причём производная f’
(x)
обращается в нуль в конечном числе
точек, лежащих внутри промежутка X.
0, причём производная f’
(x)
обращается в нуль в конечном числе
точек, лежащих внутри промежутка X.
Это условие геометрически означает, что касательная к графику монотонно возрастающей функции образует с положительным направлением оси Ox острый угол или параллельна ей (рис. 41).
Условие
убывания функции. Дифференцируемая
функция y
= f
(x)
монотонно убывает на промежутке X
тогда и только тогда, когда её производная
не положительна внутри этого промежутка:
f’
(x)
![]() 0, причём производная f’
(x)
обращается в нуль в конечном числе
точек, лежащих внутри X.
0, причём производная f’
(x)
обращается в нуль в конечном числе
точек, лежащих внутри X.
Это условие геометрически означает, что касательная к графику монотонно убывающей функции образует с положительным направлением оси Ox тупой угол или параллельный ей (рис. 42).
Экстремумы функции. Говорят, что функция y = f (x) имеет максимум в точке x1 (рис. 43), если значение функции в этой точке больше, чем её значения во всех точках, достаточно близких к x1, т. е. если f (x1 + x) f (x1) для любых x, как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом, x = x1 – точка максимума, а ymax = f (x1) – максимум функции.
Говорят, что функция y = f(x) имеет минимум в точке x2 (рис. 43), если значение функции в этой точке меньше, чем её значения во всех точках, достаточно близких к x2, т. е. если f (x2 + x) f (x2) для любых x, как положительных, так и отрицательных, но достаточно малых по модулю. Таким образом, x = x2 – точка минимума, а ymin = f(x2) – минимум функции.
Если в некоторой точке функция имеет максимум или минимум, то говорят, что в этой точке имеет место экстремум. Значение функции в этой функции называется экстремальным.




Замечание. Следует помнить: 1) что максимум (минимум) не является обязательно наибольшим (наименьшим) значением, принимаемым функцией; 2) функция может иметь несколько максимумов или минимумов; 3) функция, определённая на отрезке, может достигать экстремума только во внутренних точках этого отрезка.
Необходимое условие экстремума. Если функция y = f (x) имеет экстремум при x = x0, то её производная в этой точке равна нулю или бесконечности либо вовсе не существует, при этом сама функция в точке x0 определена.
Из этого следует, что точки экстремума функции следует разыскивать только среди тех, в которых её первая производная равна нулю, или бесконечности, или не существует. Эти точки называются критическими точками l рода.
Этот признак экстремума является только необходимым. Поэтому, определив критические точки l рода, надо каждую из них в отдельности исследовать на основании достаточных условий экстремума.
Первое достаточное условие существования экстремума функций. Пусть точка x = x0 является критической точкой lрода функции y = f (x), а сама функция дифференцируема во всех точках некоторого промежутка, содержащего эту точку (за исключением, возможно, самой этой точки). Тогда:
если при переходе слева направо через критическою точку l рода x = x0 первая производная меняет знак с плюса на минус, то в этой точке функция достигает максимума, т. е. x = x0 – точка максимума, ymax = f (x0);
если при переходе слева направо через критическую точку l рода x = x0 первая производная меняет знак с минуса на плюс, то в этой точке функция достигает минимума, т. е. x = x0 – точка минимума, ymin = f (x0);
если при переходе через критическую точку l рода первая производная не меняет знака, то в этой точке экстремума нет.





Рис. 44
Для исследования функции на экстремум по первой производной следует:
Найти область определения функции.
Найти первую производную функции и критические точки l рода.
Отметить границы области определения и критические точки l рода на числовой прямой.
Исследовать знак производной в каждом из полученных интервалов.
Выписать точки экстремума и вычислить экстремумы функции.
Пример 16. Найти экстремумы функции y = (1 – x2)3.
Решение. 1. Областью определения функции служит множество всех действительных чисел, т. е. x R. 2. Функция имеет производную всюду, поэтому определяем критические точки из условия f’ (x) = 0. Находим производную:
y’ = 3 (1 – x2)2 (1 – x2)’ = 3 (1 – x2)2 ( - 2x) = - 6x (1 – x2)2;
y’ = 0, - 6x (1 – x2)2 = 0, x1 = 0, x2 = - 1, x3 = 1.
3. Отмечаем эти критические точки на числовой прямой (рис. 44).
4. Исследуем знак производной y’ = - 6x (1 – x2)2 в каждом из полученных интервалов: y’ ( - 2) 0, y’ ( - 0,5) 0, y’ (0,5) 0, y’ (2) 0.
5. Точка x = 0 – точка максимума, так как при переходе через неё слева направо производная меняет знак с плюса на минус: ymax = y (0) = 1. Точки x = - 1 и x = 1 не являются точками экстремума.
Второе достаточное условие существования экстремума функции. Если в точке x = x0 первая производная функции равна нулю (f’ (x0) = 0), а вторая производная отлична от нуля, то x = x0 – точка экстремума.
При этом если вторая производная в этой точке положительна (f” (x0) 0), то x = x0 – точка минимума; если вторая производная в этой точке отрицательна (f” (x0) 0), x = x0 – точка максимума.
Для исследования функции на экстремум по первой и второй производной следует:
Найти область определения функции.
Найти первую производную функции и стационарные точки, т. е. точки, в которых она обращается в нуль.
Найти вторую производную функции и исследовать её знак в каждой стационарной точке.
Выписать точки экстремума и вычислить (если нужно) экстремумы функции.
Пример 17. Найти экстремумы функции f (x) = x3 – 3x2 + 1.
Решение. 1. Областью определения функции служит множество всех действительных чисел, т. е. x R. 2. Функция имеет производную всюду, поэтому критические точки определяем из условия f’ (x) = 0:
f’ (x) = 3x2 – 6x, f’ (x) = 0, 3x2 – 6x = 0,
3x (x – 2) = 0, x1 = 0, x2 = 2.
3. Находим вторую производную функции f” (x) = 6x – 6. Исследуем знак второй производной в каждой критической точке: f” (0) = - 6 0; значит, x = 0 – точка максимума, ymax = y (0) = 1;
f” (2) = 6 0; значит, x = 2 – точка минимума, ymin = y (2) = 23 – 3 ∙ 22 + 1 = 8 – 12 + 1 = - 3.
Наибольшее и наименьшее значение функции. Наибольшим значением функции называется самое большое, а наименьшим значением – самое меньшее из всех её значений.
Функция может иметь только одно наибольшее значение и только одно наименьшее значение или может не иметь их совсем.
Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:
если в некотором открытом промежутке a x b (конечном или бесконечном) функция y = f (x) непрерывна и имеет только один экстремум и если это максимум, то он и является наибольшим значением функции, а если минимум – наименьшим значением функции в этом промежутке;
если функция y = f (x) непрерывна на отрезке a x b, то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигают ею или в точках экстремума, лежащих внутри отрезка, или на концах этого отрезка.
Поэтому, чтобы найти наибольшее и наименьшее значения функции на отрезке a x b, где она непрерывна, следует:
Найти экстремумы функции на данном отрезке.
Найти значения функции на концах отрезка: f (a) и f (b).
Из всех найденных значений выбрать наибольшее и наименьшее.




Рис. 45
Пример
18.
Найти наибольшее и наименьшее значения
функции y
= ![]() x4
-
x3
-
x2
+ 2 на отрезке - 2
x
4.
x4
-
x3
-
x2
+ 2 на отрезке - 2
x
4.
Решение. 1. Найдём экстремумы функции, для чего найдём производную функции и критические точки l рода из условия y’ = 0:
y’
= ![]()
y’ = 0 при x1 = 0, x2 – 2x – 3 = 0, D = b2 – 4ac,
D
= 4 – 4 ( - 3) = 16, x
= (2 ![]() 4)/2,
x2
= - 1, x3
= 3.
4)/2,
x2
= - 1, x3
= 3.
Отметим критические точки l рода x = - 1, x = 0, x = 3 на числовой прямой (рис. 45).
Исследуем знак производной в каждом из полученных интервалов: y’ = ( - 2) 0, y’ ( - 0,5) 0, y’ (1) 0, y’ (4) 0. Таким образом,
ymin
= y
( - 1) = ![]()
ymax = y (0) = 2;
ymin
= y
(3) = ![]()
2. Найдём значения функции на концах отрезка:
y
( - 2) = ![]()
y
(4) = ![]()
Итак, наибольшее значение функции yнаиб = y ( - 2) = 5
 , а наименьшее значение функции yнаим
= y
(3) = - 9
, а наименьшее значение функции yнаим
= y
(3) = - 9  .
.
Пример 19. Требуется изготовить закрытый цилиндрический бак объёмом 250 см3. Какими должны быть его размеры, чтобы на его изготовление пошло наименьшее количество материала?
Решение. Здесь требуется определить радиус основания R и высоту H цилиндра, чтобы при заданном объёме площадь его полной поверхности была наименьшей.
Площадь полной поверхности цилиндра вычисляется по формуле
S = 2 RH + 2 R2.
Наименьшее значение этой функции и следует определить. Так как S является функцией двух независимых переменных, то одну из них надо исключить. Известно, что объём цилиндра V = R2H, или V = 250 . Выразим H через V:
H
= ![]()
Тогда
S
= 2
R
![]() S
=
S
= ![]()
Областью определения функции S являются положительные значения радиуса, т. е. R 0.
Находим производную:
S’
= - ![]() S’ = 0; при
-
S’ = 0; при
-
![]() 4
R3
= 500
,
R3
= 125, R = 5.
4
R3
= 500
,
R3
= 125, R = 5.
Находим вторую производную:
S”
= ![]()
Так как S” (5) 0, то при R = 5 имеет место минимум функции S, который и является наименьшим значением функции S. Тогда H = 250/R2, H = 250/25 = 10.
Итак, на изготовление цилиндрического бака пойдёт наименьшее количество материала, если длина радиуса основания цилиндра равна 5 см, а высота цилиндра 10 см.
Пример 20. Требуется изготовить ящик с крышкой, стороны основания которого относятся как 1 : 2, а площадь полной поверхности 108 см2. Какими должны быть его размеры, чтобы его объём был наибольшим?
Решение. Здесь требуется определить стороны основания a и b и высоту Н прямоугольного параллелепипеда, чтобы при заданной площади полной поверхности его объём был наибольшим.
По условию, a : b = 1 : 2, откуда a = x, b = 2x. Объём прямоугольного параллелепипеда равен V = ab H или V = 2x2 H. Надо исключить переменную Н. Известно, что S = 108 и S = 2Sосн + Sбок , Sбок = Росн ∙ Н. Имеем
S = 2x ∙ 2x + (x + 2x) ∙ 2H = 4x2 + 6xH, 4x2 + 6xH = 108,
6xH
= 108 – 4x2,
H = ![]()
H
= ![]()
Тогда
V
= 2x2
![]()
Наибольшее значение этой функции и следует определить.
Областью определения функции V являются положительные значения x, т. е. x 0.
Находим производную:
V’
= 36 - ![]()
V’ = 0 при 4x2 = 36, x2 = 9, x = 3.
Находим вторую производную: V” = - 8x; V” (3) 0, т. е. при x = 3 функция имеет максимум, который и служит наибольшим значением функции. При этом
H
= ![]()
Итак, объём ящика является наибольшим, если стороны его основания имеют длину 3 и 6 см, а высота 4 см.
Пример 21. Число 10 разбить на два положительных слагаемых так, чтобы сумма их кубов была наименьшей.
Решение. Пусть одно из слагаемых равно x, тогда другое слагаемое есть 10 – x. сумма кубов этих слагаемых равна
S = x3 + (10 – x)3 = x3 + 1000 – 300x + 30x2 – x3,
S = 30x2 – 300x + 1000.
Наименьшее значение этой функции и надо определить.
Областью определения функции S являются положительные значения x, т. е. x 0.
Находим производную:
S’ = 30 ∙ 2x – 300 = 60x – 300;
S’ = 0 при 60x – 3000 = 0, 60x = 300, x = 5.
Находим вторую производную S” = 60, S” (5) 0, т. е. при x = 5 функция S имеет минимум, который и является наименьшим значением функции.
Итак, число 10 надо разложить на два равных слагаемых: 5 и 5.
Пример 22. Закон прямолинейного движения тела задан уравнением s = - t3 + 9t2 – 24t – 8 (s – в метрах, t – в секундах). Найти максимальную скорость движения тела.
Решение. Скорость движения тела в данный момент времени равна производной пути s по времени t:
(t) = s’ = - 3t2 + 18t – 24.
Исследуем эту функцию на экстремум с помощью второй производной: ’(t) = - 6t + 18, ” (t) = - 6. Вторая производная отрицательна; следовательно, скорость является наибольшей при t = 3.
Максимальная скорость движения составляет
(3) = - 3 ∙ 32 + 18 ∙ 3 – 24 = - 27 + 54 – 24 = 3, max = 3 м/с
Направление
вогнутости и точки перегиба кривой.
Говорят, что на промежутке a
x
b
кривая обращена выпуклостью вверх или
выпукла (![]() )
если она лежит ниже касательной,
проведённой в любой её точке (рис. 46).
)
если она лежит ниже касательной,
проведённой в любой её точке (рис. 46).
Говорят,
что на промежутке b
x
c
кривая обращена выпуклостью
вниз или
вогнута
(![]() ),
если она лежит выше касательной,
проведённой в любой её точке (рис. 46).
),
если она лежит выше касательной,
проведённой в любой её точке (рис. 46).
Точкой перегиба непрерывной кривой называется точка А (рис. 46), при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот.
Достаточное условие выпуклости (вогнутости) кривой. График дифференцируемой функции y = f (x) является выпуклым на промежутке a x b, если вторая производная функции отрицательна в каждой точке этого промежутка: f” (x) 0 при a x b.
График дифференцируемой функции y = f (x) является вогнутым на промежутке b x c, если вторая производная функции положительна в каждой точке этого промежутка: f” (x) 0 при b x c.
Точки, в которых вторая производная функции равна нулю, или бесконечности, или не существует, называются критическими точками ll рода.
Если при переходе через критическую точку ll рода x = x0 вторая производная функции меняет знак, то x = x0 – абсцисса точки перегиба. Ордината точки перегиба равна значению функции в точке x0. Точка (x0, f (x0)) – точка перегиба графика функции y = f (x).









Рис. 46
Чтобы найти направление вогнутости и точки перегиба кривой, следует:
1.Найти область определения функции.
2.Найти вторую производную функции и критические точки ll рода.
3.Отметить границы области определения и критические точки ll рода на числовой прямой.
4.Исследовать знак второй производной в каждом из полученных интервалов.
5.Записать промежутки выпуклости и вогнутости, абсциссу точки перегиба и вычислить её ординату.
Пример 23. Определить направление вогнутости и точки перегиба кривой y = x4 + 2x3 – 12x2 – 5x + 2.
Решение. 1. Областью определения функции служит множество всех действительных чисел, т. е. x R. 2. Найдём вторую производную функции и критические точки ll рода из условия y” = 0:
y’ = 4x3 + 2 ∙ 3x2 – 12 ∙ 2x – 5 = 4x3 + 6x2 – 24x – 5;
y” = 4 ∙ 3x2 + 6 ∙ 2x – 24 = 12x2 + 12x – 24;
y” = 12 (x2 + x – 2);
y” = 0 при x2 + x – 2 = 0,
x1,2
=
![]() x1
= - 2, x2
= 1.
x1
= - 2, x2
= 1.
3 Отметим критические точки ll рода x = - 2 и x = 1 на числовой прямой (рис. 47).
4 Исследуем знак второй производной в каждом из полученных интервалов: y” ( - 3) 0, y” (0) 0, y” (2) 0.
5 Кривая вогнута при x - 2 и x 1; кривая выпукла при – 2 x 1;
xт.п = - 2, yт.п = y ( - 2) = 16 – 2 ∙ 8 – 12 ∙ 4 + 5 ∙ 2 + 2 = - 36;
xт.п = 1, yт.п = y (1) = 1 + 2 – 12 – 5 + 2 = - 12.
Точки перегиба ( - 2, - 36), (1, - 12).






Рис. 47 Рис. 48
Общая схема исследования функций и построения их графиков.
1.Найти область определения функции и поведение функции в границах области определения.
2.Выяснить вопрос о чётности, нечётности и периодичности функции.
3.Найти точки пересечения графика функции с осями координат.
4.Найти промежутки монотонности и экстремумы функции.
5.Найти направление вогнутости и точки перегиба графика функции.
6.Построить график функции, используя все полученные результаты исследования. Если их окажется недостаточно, то следует найти ещё несколько точек графика функции, исходя из её уравнения.
Построение графика функции целесообразно выполнять по его элементам, вслед за выполнением отдельных пунктов исследования.
Пример
24.
Построить график функции y
= ![]() .
.
Решение.
1.
Областью определения функции служит
множество всех действительных чисел,
т. е. x
R.
Далее, находим ![]()
![]() 2. Выясняем вопрос о чётности или
нечётности функции:
2. Выясняем вопрос о чётности или
нечётности функции:
f
( - x)
= ![]() ,
f
( - x)
,
f
( - x)
![]() f
(x),
f
( - x)
- f
(x).
f
(x),
f
( - x)
- f
(x).
Значит, функция не является ни чётной, ни нечётной. 3. Найдём точки пересечения графика функции с осями координат:
Ox:
![]()
![]() Oy:
Oy:
![]()
Находим промежутки монотонности и экстремумы функции:
y’
= (![]()
y’ = 0 при x1 = 0 и x2 = 3.
Отметим критические точки l рода x = 0 и x = 3 на числовой прямой (рис. 48) и исследуем знак производной в каждом из полученных интервалов: y’ ( - 1) 0, y’(1) 0, y’ (4) 0.
Функция возрастает при x 3 и убывает при x 3; x = 3 – точка максимума,
ymax
= y (3) = ![]()
Находим направление вогнутости и точки перегиба графика функции:
y”
= (![]()
Итак, y” = 0 при x1 = 0, x2 = 2.
Отметим критические точки ll рода x = 0 и x = 2 на числовой прямой (рис. 49) и исследуем знак второй производной в каждом из полученных интервалов: y” ( - 1) 0, y” (1) 0, y” (3) 0.
График функции является выпуклым при x 0 и x 2 и вогнутым при 0 x 2;
Xт.п = 0, yт.п = y (0) = 0;
Xт.п
= 2,
yт.п
= y
(2) = ![]()
Точки перегиба графика функции (0, 0) и (2; 3, 2).
Отметим
все полученные точки в системе координат
и соединим их плавной кривой (рис. 50).





Рис. 49 Рис.50
Для уточнения графика найдём дополнительную точку y ( - 1) – 1.
Неопределенный интеграл
Понятие
неопределенного интеграла. Напомним,
что дифференцирование-это действие, с
помощью которого по данной теме функции
находиться её производная или дифференциал.
Например, если ![]() ,
то
,
то ![]() ,
,
![]()
Как
мы знаем, нахождение производной имеет
большое практическое значение. Так, по
данному закону движения тела s=s(t)
мы путем дифференцирования находили
скорость ![]() ,
а затем и ускорение
,
а затем и ускорение ![]() по данному уравнению кривой
по данному уравнению кривой ![]() определяли угловой коэффициент
касательной, проведенной к этой кривой:
определяли угловой коэффициент
касательной, проведенной к этой кривой:
![]() .
.
На
деле, однако, часто приходиться решать
обратную задачу: по известной скорости
движение тела устанавливать закон его
движения, по данному угловому коэффициенту
касательной к кривой находить уравнения
этой кривой и т.п., иначе говоря, по данной
производной отыскивать функцию, от
которой найдена эта производная, т. е.
выполнять действие, обратное
дифференцированию. Это действие
называется интегрированием.
С помощью интегрирования по данной
производной или дифференциалу Функции
находиться сама функция. Например, если
![]() ,
то
,
то ![]() ,
так как
,
так как ![]() ,.
,.
Дифференцируемая
Функция ![]() ,
,
![]() называется
первообразной
для
функции
называется
первообразной
для
функции ![]() на
интервале
,
если
на
интервале
,
если ![]() для
каждой
.
для
каждой
.
Так,
для функции ![]() первообразной
служит функция
первообразной
служит функция ![]() ,
поскольку
,
поскольку ![]() .
.
Для заданной функции ее первообразная определяется неоднозначно.
Справедлива
теорема: если
- первообразная
для
на
некотором
промежутке,
то и функция
![]() ,
где
C
– любая
постоянная, также является
первообразной
для функции
на
этом промежутке.
Обратно: каждая функция для
в данном промежутке, может быть записана
в виде
.
,
где
C
– любая
постоянная, также является
первообразной
для функции
на
этом промежутке.
Обратно: каждая функция для
в данном промежутке, может быть записана
в виде
.
Значит, достаточно найти для данной функции только одну первообразную функцию , чтобы знать все первообразные, так как они отличаются друг от друга только на постоянную величину.
Совокупность
![]() всех
первообразных функций
на интервале
называют неопределенным
интегралом
от функции
на этом интервале и пишут
всех
первообразных функций
на интервале
называют неопределенным
интегралом
от функции
на этом интервале и пишут ![]() .
Здесь
.
Здесь ![]() – подынтегральное выражение; x
– переменная интегрирования; C
– произвольная постоянная.
– подынтегральное выражение; x
– переменная интегрирования; C
– произвольная постоянная.
Например,
![]() ,
так как
,
так как ![]() .
.
Если
функция
имеет
на некотором промежутке хотя бы одну
первообразную, то ее называют интегрируемой
на этом промежутке.
Можно доказать, что любая функция,
непрерывная на отрезке ![]() ,
интегрируема на этом отрезке.
,
интегрируема на этом отрезке.
Свойства неопределенного интеграла
Производная неопределенного интеграла равна подынтегральной функции; дифференциал неопределенного интеграла равен подынтегральному выражению:
 ,
,

Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т.е.
![]() .
.
Постоянный множитель можно выносить за знак неопределенного интеграла:
 .
.Неопределенный интеграл от алгебраической суммы функций равен такой же алгебраической сумме неопределенных интегралов от каждой функции:
 .
.
Основные формулы интегрирования ( табличные интегралы ).
Из
каждой формулы дифференцирования
вытекает соответствующая ей формула
интегрирования. Например, из того, что
![]() ,
следует равенство
,
следует равенство
![]() .
.
Ниже приведена таблица основных интегралов:
 .
. .
. .
.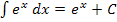 .
. .
. .
. .
.

Справедливость этих формул можно проверить дифференцированием.
Непосредственное интегрирование. Под непосредственным интегрированием понимают такой способ интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.
Пример
1. Найти
интеграл![]() .
.
Решение.
Воспользуемся определением степени с
отрицательным показателем ![]() и найдем неопределенный интеграл от
степени:
и найдем неопределенный интеграл от
степени:
![]() .
.
Пример
2. Найти
интеграл![]() .
.
Решение.
Воспользуемся определением степени с
дробным показателем ![]() и
найдем неопределенный интеграл от
степени:
и
найдем неопределенный интеграл от
степени:
![]() .
.
Пример
3. Найти
интеграл ![]() .
.
Решение.
Воспользуемся определением степени с
дробным и отрицательным показателем и
правилом умножения степеней с одинаковыми
основаниями ![]() и найдем неопределенный интеграл от
степени:
и найдем неопределенный интеграл от
степени:

![]() .
.
Пример
4.
Найти интеграл![]() .
.
Решение.
Воспользуемся определением степени с
дробным показателем![]() ,
правилами действий над степенями с
одинаковыми основаниями
,
,
правилами действий над степенями с
одинаковыми основаниями
,![]() правилом деления суммы на число и найдем
интеграл от каждого слагаемого отдельно.
Имеем
правилом деления суммы на число и найдем
интеграл от каждого слагаемого отдельно.
Имеем
 .
.
Заметим, что произвольные постоянные, входящие по определению в каждый из слагаемых неопределенных интегралов, объединяются в одну произвольную постоянную.
Пример
5.
Найти интеграл ![]()
Решение.
Раскроем скобки по формуле ![]() и
неопределенный интеграл от полученной
алгебраической суммы функций заменим
такой же алгебраической суммой
неопределенных интегралов от каждой
функции:
и
неопределенный интеграл от полученной
алгебраической суммы функций заменим
такой же алгебраической суммой
неопределенных интегралов от каждой
функции:
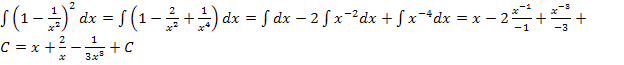 .
.
Примет
6. Найти
интеграл ![]() .
.
Решение.
Для нахождения интеграла воспользуемся
формулой![]() и
свойствами неопределенного интеграла:
и
свойствами неопределенного интеграла:![]() .
.
Интегрирование методом подстановки. Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом пользуются методом подстановки.
Сущность этого метода заключается в том, что путем введения новой переменной удается свести данный интеграл к новому интегралу, который сравнительно легко берется непосредственно.
Для интегрирования методом подстановки можно использовать следующую схему:
часть подынтегральной функции надо заменить новой переменной;
найти дифференциал от обеих частей замены;
все подынтегральное выражение выразить через новую переменную (после чего получиться табличный интеграл);
найти полученный табличный интеграл;
сделать обратную замену.
Пример
7.
Найти интеграл![]() .
.
Решение.
Произведем подстановку 5—3x=
t,
тогда —3dx=dt,
откуда ![]() .
Далее получаем
.
Далее получаем ![]() .
.
Пример
8. Найти
интеграл
![]() .
.
Решение.
Сначала положим 2+cos
x=t,
тогда —sin
x
dx=dt,
откуда sin
x
dx=—dt.
Далее получаем ![]() .
.
Пример
9. Найти
интеграл
![]() .
.
Решение.
Положим![]() ,
тогда
,
тогда![]() от
куда
от
куда![]() .
Далее получаем
.
Далее получаем
![]() .
.
Пример
10. Найти
интеграл![]() .
.
Решение.
Положим![]() ,
тогда
,
тогда![]() ,
откуда
,
откуда![]() .
Далее получаем
.
Далее получаем
![]() .
.
В
практике интегрирования часто встречаются
интегралы, для нахождения которых можно
использовать следующие формулы![]() :
:
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
Так,
при нахождении
можно
использовать формулу![]() ,
где
,
где
![]() .
Тогда
.
Тогда![]() .
.
