
- •1 Глава
- •1.Лоогические символы в математике (базисные типы высказываний).
- •2.Логические символы в математике (пропозиционные связки, конъюнкция, дизъюнкция).
- •3. Логическое символы в математике (пропорц. Связки- импликация,достаточность, эквивалентость, отрицание).
- •1.Пропозиционные связки- это операция математической логики сходная с используемыми в обычной речи союзами «или», «и», «если», «то», «тогда», «когда», а также с отрицанием.
- •4.Логические символы в математике ( кванторы, скобки).
- •5.Логические символы в математике (таблицы истинности).
- •6.Понятие множества.
- •7. Равенство множеств, подмножества, пустое множество, основные числовые множества.
- •8. Объединение и пересечение множеств.
- •12.Декартово произведение множеств.
- •13. Бинарные отношения.
- •14. Основные свойства, которыми обладают бинарные отношения.
- •15.Отношения эквивалентности и порядка.
- •16. Отображение.
- •17. Частные случаи отображений
- •18. Композиция отображений, тождественное отображение.
- •19.Функция, последовательность,функционал.
- •2 Глава.
- •1.Величина и ее измерение.
- •2.Постоянные и переменные величины.
- •3.Изменение переменной величины, переменные величины- дискретные и меняющиеся в промежутке.
- •4.Бесконечно малая величина.
- •5.Предел переменной величины.
- •6.Основные теоремы о пределах
- •7.Бесконечно большая величина.
- •8. Монотонная переменная. Теорема Вейерштрасса.
- •9.Предел функции и ее геометрический смысл.
- •10.Обобщение понятия предела функции.
- •11.Непрерывность и разрывы функции.
- •12.Первый замечательный предел.
- •Глава 3. Дифференциальное исчисление.
- •Производная, ее геометрический и физический смысл.
- •Правила дифференцирования.
- •Теорема Ферма.
- •Теорема Ролля.
- •Teoрeмa Коши, правило Лопиталя.
- •Правила отыскания экстремумов функции.
Правила отыскания экстремумов функции.
Пусть функция y=f(x) определена и дифференцируема в некотором промежутке. Сформулируем правила отыскания экстремумов, т.е. максимумов и минимумов.
П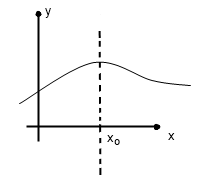 усть
в точке х=х0
функция достигает максимума, тогда при
x<х0
функция f(x)
возрастает, т.е. её производная f’(x)>0.
При х=х0,
f’(x)=0
( по т.Ферма)
усть
в точке х=х0
функция достигает максимума, тогда при
x<х0
функция f(x)
возрастает, т.е. её производная f’(x)>0.
При х=х0,
f’(x)=0
( по т.Ферма)
П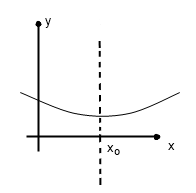 ри
x>х0
функция убывает, т.е. f’(x)<0,
т.о. в точке максимума производная меняет
знак с + на -.
ри
x>х0
функция убывает, т.е. f’(x)<0,
т.о. в точке максимума производная меняет
знак с + на -.
Аналогично:
Пусть в точке х=х0 функция достигает минимума, тогда при x<х0 производная f’(x)<0. При х=х0, f’(x)=0 ( по т.Ферма)
При x>х0 функция убывает, т.е. f’(x)>0, т.о. в точке минимума производная меняет знак с - на +.
1 правило отыскание экстремумов:
Составить производную функции y’=f’(x).
Приравниваем производную к нулю f’(x)=0 и решаем уравнение, находим точки х=х0, подозрительные на экстремум.

 Исследуем
эти точки по таблице:
Исследуем
эти точки по таблице:
х0 |
х0-∆х |
х0 |
х0+∆х |
Вывод |
f’(x) |
+ |
0 |
- |
максимум |
f’(x) |
- |
0 |
+ |
минимум |
f’(x) |
+ |
0 |
- |
Точка перегиба ↑(возрастание) |
f’(x) |
- |
0 |
+ |
Точка перегиба ↓(убывание) |
В точке максимума производная меняет знак + на -, т.е.
f’(x) ↓, а производная убывающий функции отрицательна, т.е. в точке максимума f’’(x)<0.
Аналогично в точке минимума f’(x) меняет знак с – на +, поэтому f’’(x)>0.
Отсюда получаем 2ое правило отыскания экстремумов функции:
Составить производные первого и второго порядков.
Приравнять производные к 0. Найти точки х0 подозрительные на экстремумы.
Исследуем точки по таблице.
х0 |
f’(x) |
f’’(x) |
Вывод |
х0 |
0 |
- |
максимум |
х0 |
0 |
+ |
минимум |
х0 |
0 |
0 |
Сомнительный случай (исп. 1ое правило) |
В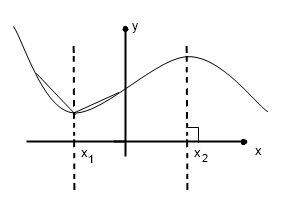 точке х1 производной не существует, т.к.
нет единого направления касательной.
А в точке х2 производная равна бесконечности,
т.к. f’(x)=tgα,
а tg90◦=∞.
точке х1 производной не существует, т.к.
нет единого направления касательной.
А в точке х2 производная равна бесконечности,
т.к. f’(x)=tgα,
а tg90◦=∞.
У
 равнение
прямой с угловым коэффициентом. Уравнение
касательной функции. Асимптоты и их
уравнения.
равнение
прямой с угловым коэффициентом. Уравнение
касательной функции. Асимптоты и их
уравнения.
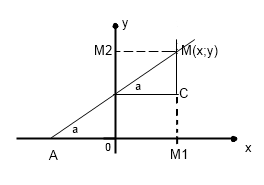
Выведем уравнение прямой, проходящей под углом α к положительному направлению ОХ и отсекающей на оси OY отрезок OB=b.
![]() OAB=α
; tgα=k-угловой
коэффициент
OAB=α
; tgα=k-угловой
коэффициент
OB=b; OM1=x; OM2=y
MM1=MC+CM1=OB+BM2=OB+BC*tg CBM;
MM1=OM2=y; y=b+x* tgα
Y=kx+b (1) - уравнение прямой с угловым коэффициентом.
Пусть прямая проходит через точку Mo(xo;yo), тогда координаты удовлетворяют условию yo=kxo+b (2)
Вычтем из равенства (1) равенство (2): y-yo=k(x-xo) (3)- уравнение прямой, проходящей через данную точку в данном направлении.
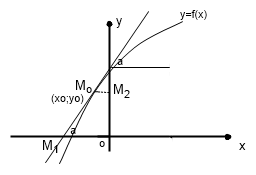 По
геометрическому смыслу f’(x)-
производная f’(x0)-
это тангенс угла наклона касательной
графика функции к оси OX,равный
k.
По
геометрическому смыслу f’(x)-
производная f’(x0)-
это тангенс угла наклона касательной
графика функции к оси OX,равный
k.
Т.о. уравнение в точке Mo(xo;yo) имеет вид:
y-f(x0)=f’(x0)*(x-x0), т.к. yo=f(x0), а k= f’(x).
Т.о. мы нашли уравнение касательной к графику функции.
О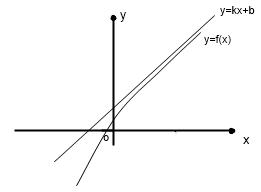 пр.
Асимптота кривой с бесконечной ветвью
это такая прямая, что расстояние точки
кривой от этой прямой безгранично
уменьшается, при удалении точки по
бесконечной ветви.
пр.
Асимптота кривой с бесконечной ветвью
это такая прямая, что расстояние точки
кривой от этой прямой безгранично
уменьшается, при удалении точки по
бесконечной ветви.
П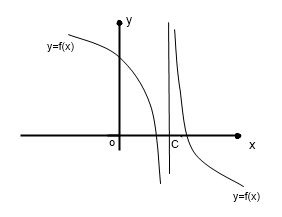 усть
в точке х=с функция y=f(x)
имеет разрыв второго рода.
усть
в точке х=с функция y=f(x)
имеет разрыв второго рода.
Прямая х=с- вертикальная асимптота к графику функции.
Могут быть также наклонные асимптоты к графику функции.
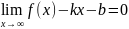 ;
;
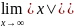 (4);
(4);
k=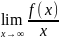 -
угловой коэффициент асимптоты.
-
угловой коэффициент асимптоты.
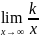 =0;
=0;
b=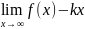 (5); Если пределы (4) и (5) существуют и
конечны, то существует асимптота к
графику функции: y=kx+b,
причём если k=0,
то y=b-горизонтальная
асимптота.
(5); Если пределы (4) и (5) существуют и
конечны, то существует асимптота к
графику функции: y=kx+b,
причём если k=0,
то y=b-горизонтальная
асимптота.
Е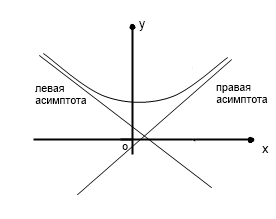 сли
пределы (4) и (5) различны, то существуют
2 асимптоты: правая и левая, которые
иногда могут сливаться в одну асимптоту.
сли
пределы (4) и (5) различны, то существуют
2 асимптоты: правая и левая, которые
иногда могут сливаться в одну асимптоту.
