2. Правила дифференцирования.

Используя определение производной, выраженное формулой (1) найдем правила дифференцирования, т.е. правила вычисления производной.

1. Пусть у=C, тогда f(х)=С и f(х+▲х)=С =>

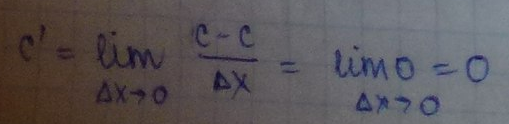
2. С’=0 (4) Производная постоянной величины равна 0.

3. Пусть у=х

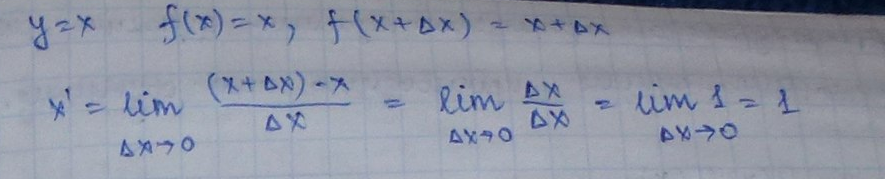Производная аргумента равна 1.

3) Пусть у=CU(х)

[CU(x)]’= CU’(x) (6) Постоянный множитель выносится за знак производной.

4) у=U(х)± υ(х)

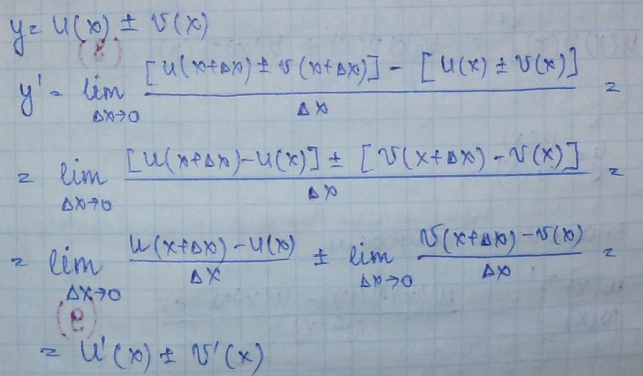
[U(х)±υ(х)]’=U’(х) ± υ’(х) (7) Производная алгебраической суммы функции равна алгебраической сумме производных этих функций.

5) Найдем производную у=U(x)*υ(х)

[U(х) υ(х)]’= U’(х) υ(х) + U(x) υ’(х) (8)

6) у= ^U(x)\_υ(х)

Аналогично получаем

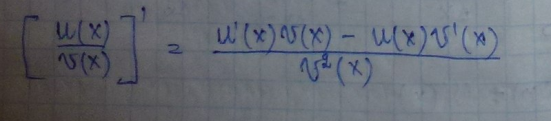
1. у=sin x

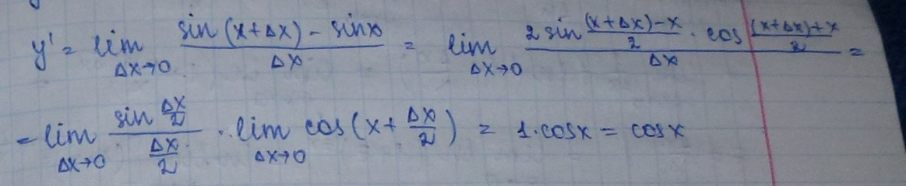
(sin x)’= cos x (10)

2. y=cos x

3. Таким образом, получаем: (cos x)’= sin x (11)

4. y=tg x= sin x\ cos x

Для вычисления производной от tg используем формулу (9):

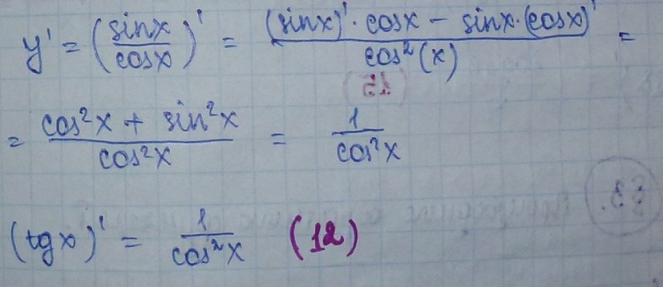
5. y=ctg x= cos x \sin x

Таким образом, получаем: (13)

6. y=ln x

(ln x)’= 1\x (14)

7. y=log_ax=ln e·log_ae

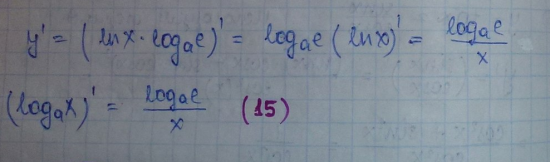
3. Производные обратных функций.

4. Производные сложных функций.

5. Дифференциалы первого порядка

6. Производные и дифференциалы высших порядков.

7. Максимумы и минимумы функций, супремум и инфинум функций.

Опр.10. Функция y=f(x) имеет в точке x=x(0)максимум, если ее значение в этой точке больше всех ее значений в достаточно малой E-окрестности этой точки, т.е. f(x0) > f(x0+E) при E>0 и E<0 (52)

Функция y=f(x) имеет в точке x=x0 минимум, если ее значение в этой точке меньше всех ее значений в достаточно малой окрестности этой точки, т.е. f(x0) < f(x0+E), где E>0 и E<0 (53)

Понятия максимума и минимума объединяются общим понятием экстремума функции.

Опр.11. Наибольшее значение функции y=f(x) на промежутке [a,b] называется супремумом и обозначается:

sup{f(x)}, x принадлежит [a,b],

а наименьшее значение функции y=f(x) на [a,b] называется инфимумом и обозначается:

inf {f(x)}, x принадлежит [a,b].

Супремум функции может достигаться либо в точке максимума, либо на конце промежутка, либо в точке разрыва. А инфимум функции может достигаться либо в точке минимума, либо на конце промежутка, либо в точке разрыва.

8. Теорема Ферма.

Если функция y=f(x) определена и непрерывна в открытом промежутке (a,b), имеет в каждой точке этого промежутка конечную производную и в некоторой точке x=c, принадлежащей (a,b), достигает экстремума, то производная функции в этой точке равна нулю, т.е. f ’( c ) = 0.

Доказательство:

Докажем теорему для случая максимума. Тогда, согласно формуле 52,

f(c+E) – f( c ) < 0 при E>0 b E<0, следовательно

( f(c+E) – f ( c ) )/ E <0 при E>0,

( f(c+E) – f ( c ) )/ E >0 при E<0.

Перейдем в этих равенствах к пределу при Е, стремящемся к 0, и используем определение производной, тогда по теореме 5 главы 2 находим:

lim ( f(c+E) – f( c) ) / E = f ‘ (c ) <= 0 (E стремится к +0)

lim ( f(c+E) – f( c) ) / E = f ‘ (c ) >= 0 (E стремится к -0),

следовательно, чтобы выполнялись оба неравенства, необходимо, чтобы f ‘ ( c ) =0.

Следствие:

Касательная к графику функции в точках экстремумов параллельна оси ОХ.

Доказательство: В соответствии с геометрическим смыслом производной, производная в некоторой точке численно равна tg угла наклона касательной к графику этой функции по отношению к оси ОХ => в точке экстремума

tg альфа = 0 => альфа=0 , т.е. касательная параллельна оси ОХ.