
- •Система двух линейных уравнений с двумя неизвестными. Совместные и несовместные системы.
- •Вывод формулы Крамера решения системы второго порядка.
- •4.Исследование системы 2-ого порядка с помощью определителей. Геометрическая интерпретация.
- •5. Минор, дополнительный к выделенному элементу матрицы. Алгебраическое дополнение к выделенному элементу матрицы.
- •6. Вычисление определителя 3-го порядка разложением по элементам строки или столбца.
- •7. Решение системы линейных уравнений 3-го порядка. Условие
- •Решение системы линейных алгебраических уравнений методом Крамера
- •10. Однородные системы. Условие существования нейтральных решений и их нахождение.
Система двух линейных уравнений с двумя неизвестными. Совместные и несовместные системы.
Системы двух линейных уравнений с двумя неизвестными имеют вид:

где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами.
Метод подстановки.
1) Из одного уравнения выражаем одно из неизвестных, например x, через коэффициенты и другое неизвестное y:
x = ( c – by ) / a . (2)
2) Подставляем во второе уравнение вместо x :
d ( c – by ) / a + ey = f .
3) Решая последнее уравнение, находим y :
y = ( af – cd ) / ( ae – bd ).
4) Подставляем это значение вместо y в выражение (2) :
x = ( ce – bf ) / ( ae – bd ) .
Сложение или вычитание. Этот метод состоит в следующем.
1) Умножаем обе части 1-го уравнения системы (1) на (– d ), а обе части 2-го уравнения на а и складываем их:

Отсюда получаем: y = ( af – cd ) / ( ae – bd ).
2) Подставляем найденное для y значение в любое уравнение системы (1):
ax + b( af – cd ) / ( ae – bd ) = c.
3) Находим другое неизвестное: x = ( ce – bf ) / ( ae – bd ).
Совместные и несовместные системы.
Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1 + x2
+ x2
 +
… + xn
+
… + xn
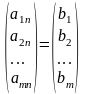
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример. Определить совместность системы линейных уравнений.
 А
=
А
=
 ;
;
 = 2 + 12 = 14
0; RgA
= 2;
= 2 + 12 = 14
0; RgA
= 2;
A*
=

 RgA*
= 2.
RgA*
= 2.
Система совместна. Решения: x1 = 1; x2 =1/2.
Пример. Определить совместность системы линейных уравнений:

A
=

~
 .
.
 RgA
= 2.
RgA
= 2.
A*
=
 RgA*
= 3.
RgA*
= 3.
Система несовместна.
Матрицы коэффициентов системы. Определитель 2-ого порядка.
Матрицы коэффициентов системы.
Систему из m уравнений с n неизвестными

можно представить в матричном виде

и тогда всю систему можно записать так:
AX = B,
где A имеет смысл таблицы коэффициентов aij системы уравнений.
Если m = n и матрица A невырожденная, то решение этого уравнения состоит в нахождении обратной матрицы A − 1, поскольку умножив обе части уравнения на эту матрицу слева
A − 1AX = A − 1B
A − 1A — превращается в E (единичную матрицу). И это даёт возможность получить столбец корней уравнений
X = A − 1B.
Все правила, по которым проводятся операции над матрицами, выводятся из операций над системами уравнений.
Определитель 2-ого порядка.
Число ![]() называется
определителем второго порядка,
соответствующего таблице (1). Этот
определитель обозначается символом
называется
определителем второго порядка,
соответствующего таблице (1). Этот
определитель обозначается символом  ;
соотвественно имеем
;
соотвественно имеем
 .
(2).
.
(2).
