1. Критерий двудольности графа.

Теорема 8.1 (Кёниг, 1936 г.). Для двудольности графа необходимо и достаточно, чтобы он не содержал циклов нечетной длины.

 Необходимость. Пусть G — двудольный граф, C — один из его циклов длины k. Пройдем все ребра этого цикла в той последовательности, в какой они на нем расположены, начиная с некоторой вершины v. Сделав k шагов, вернемся в v. Так как концы каждого ребра лежат в разных долях, то k — четное число. Достаточность. Не ограничивая общности, можно рассматривать только связные графы, т. к. дизъюнктное объединение двудольных графов также двудольно. Пусть связный граф G порядка n > 1 не имеет циклов нечетной длины. Построим разбиение вершин графа VG = A  B относительно вершины v  VG следующим образом: произвольную вершину u отнесем к классу A, если расстояние d(u, v) — четное число, и к классу B, если это расстояние нечетно. Покажем, что порожденные подграфы G(A) и G(B) являются пустыми. Пусть, напротив, существуют две смежные вершины u и w, входящие в один класс, т. е. d(v, u) = d(v, w). Ясно, что ни одна из них не совпадает с v, так как v  A, а смежные с ней вершины находятся B. Пусть v₁ — последняя, считая от v, общая вершина (v, u)-цепи и (v, w)-цепи. Так как эти цепи имеют начальные (v, v₁)-подцепи одинаковой длины, то (v₁, u)-подцепь и (v₁, w)-подцепь будут иметь одинаковую длину. Объединяя эти подцепи и ребро uw, получим цикл нечетной длины. 

Следствие 8.2. Граф является двудольным тогда и только тогда, когда он не имеет простых циклов нечетной длины.

2. Число всех беспорядков на множестве {1,2,…,n}.

Теорема 10.4. Число | D_n | всех беспорядков на множестве {1, 2,…, n} равно =

 Рассмотрим множества , i = 1, 2,…, n. Тогда перестановка  является беспорядком тогда и только тогда, когда . Согласно формуле включения и исключения, имеем

Для произвольной последовательности пересечение есть множество таких перестановок , для которых (j) = j для 1  j  i. Поэтому . Заметив, что последовательность 1  p₁ < p₂ <…< p_i  n можно выбрать способами, в итоге имеем



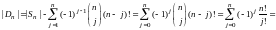
БИЛЕТ 4

1. Реберный граф и его свойства.

Для произвольного графа G реберный граф L(G) определяется следующими двумя условиями:

1) вершины L(G) ставятся в соответствие ребрам G, т.е. VG(L(G)) = EG,

2) вершины e₁ и e₂ смежны в L(G) тогда и только тогда, когда ребра e₁ и e₂ смежны в G.

Утверждение 9.1. Если d₁, d₂, …, d_n есть степенная последовательность (n, m)-графа G, то L(G) является (m, l)-графом, где .

 Ясно, что i-я вершина графа порождает ребер графа L(G), поэтому 

Очевидно, что если графы G и H изоморфны, то L(G) и L(H) также изоморфны. В то же время справедливы соотношения L(K₃)  L(K_1,3) = K₃ . Уитни доказал, что K₃ и K_1,3 — единственная пара несовпадающих связных графов, имеющих один и тот же реберный граф. Если порядок хотя бы одного из рассматриваемых графов меньше пяти, то это проверяется непосредственно, а для графов больших порядков вытекает из следующей теоремы.

Теорема 9.2 (Х. Уитни, 1932 г.). Пусть G и H — связные графы, |VG| > 4, |VH| > 4 и L(G)  L(H) . Тогда G  H .

Известно, что не всякий граф является реберным, например, звезда K_1,3 не есть реберный граф.

2. Формула включений и исключений.

Теорема 10.1. (формула включений и исключений).

(9)

 Каждый x элемент из дает единицу в . Покажем, что такой же вклад x вносит в правую часть равенства (9). Пусть, для определенности, x входит ровно в m множеств: . Тогда элемент x подсчитывается в правой части (9)

(10)

раз. Легко заметить, что из формулы бинома Ньютона для (a + b)ⁿ при a = 1 и b = –1 следует

Используем его для преобразования выражения (10):



БИЛЕТ 5