2. Формула для числа сюръективных отображений , не включающая чисел Стирлинга.

Теорема 10.2. Если | X | = m и | Y | = n, то число Z(m, n) всех сюръективных отображений f : X  Y равно

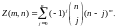
 Пусть Y={y₁, …, y_n}. Обозначим через A_i множество таких функций f : X  Y, для которых y_i  f (X). Тогда f не сюръективное отображение, если и только если f  A₁…A_n. Поскольку всего имеется n^m произвольных отображений f : X  Y, то нам достаточно определить мощность A₁... A_n.

Для произвольной последовательности 1  p₁ < p₂ <…< p_i  n пересечение 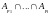есть множество функций f : X  Y таких, что y_p1, y_p2,…, y_pi  f (X). Следовательно, мощность этого пересечения равна (n – i)^m (количество функций f : X  Y \ {y_p1, y_p2,…, y_pi}). Но i-элементное множество {y_p1, y_p2,…, y_pi} Y мы можем выбрать 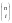способами, и тогда по формуле включения и исключения



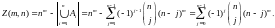
БИЛЕТ 2

1. Степенная последовательность графа. Лемма о рукопожатиях. Критерий графичности последовательности.

Степенью вершины графа G называется число инцидентных ей ребер, т. е. число вершин в ее окружении. Будем обозначать степень вершины v через deg(v) (или deg v). Тем самым deg v = |N(v)|. Максимальная и минимальная степени вершин графа G обозначаются символами (G) и (G) соответствен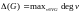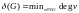но: _, .Список степеней вершин графа называется его степенной последовательностью. Порядок членов в этой последовательности роли не играет. Вершина степени 0 называется изолированной, вершина степени 1 — концевой (или висячей). Ребро, инцидентное концевой вершине, также называется концевым. Рассмотрим сумму степеней всех вершин графа. Каждое ребро вносит в эту сумму 2, поэтому верно

Утверждение 5.1 («лемма о рукопожатиях»). Сумма степеней всех вершин графа — четное число, равное удвоенному числу ребер:

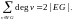
Возможная интерпретация этой леммы такова: поскольку в каждом рукопожатии участвуют две руки, то при любом числе рукопожатий общее число пожатых рук четно (при этом каждая рука учитывается столько раз, во скольких рукопожатиях она участвовала).

Следствие 5.2. В любом графе число вершин нечетной степени четно.

Понятие степени вершины и лемма о рукопожатиях cохраняются для мульти- и псевдографов. При этом каждая петля вносит в степень соответствующей вершины двойку.

Граф называется регулярным (или однородным), если степени всех его вершин равны; степенью регулярного графа называется степень его вершин. Степень регулярного графа G обозначается через deg G.

1) n – 1  d₁  d₂  …  d_n ,

2) d₁ + d₂ +… + d_n — четное число.

Теорема 5.3 (П. Эрдёш, Т. Галлаи, 1960 г.). Правильная n-последовательность d является графической тогда и только тогда, когда для каждого k = 1,2,…,n – 1 верно неравенство

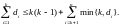
При тестировании последовательности с помощью этого критерия нет необходимости проверять все n – 1 неравенств. Установлено, что достаточно проверить k(d) = max{i : d_i  i} первых неравенств.

2. Теорема о центре дерева. Цикломатическое число графа.

Теорема 10.3. Центр любого дерева состоит из одной или из двух смежных вершин.

 Доказательство проведем индукцией по числу вершин дерева. Очевидно, что концевые вершины дерева T являются центральными только для T = K₁ или T = K₂. Пусть T — дерево порядка n > 2. Удалив из T все концевые вершины, получим дерево T’, в котором по предположению индукции центр состоит из одной или из двух смежных вершин. Заметим, что для любой вершины дерева ее эксцентриситет всегда равен расстоянию до некоторой висячей вершины. Тогда эксцентриситет каждой вершины в T’ на единицу меньше ее эксцентриситета в дереве T. Следовательно, центры деревьев T и T’ совпадают. 

Число (G) = m – n + k называется цикломатическим числом графа G. Очевидно следствие

Следствие 10.5. а) граф является лесом тогда и только тогда, когда (G) = 0; б) граф G имеет единственный цикл тогда и только тогда, когда (G) = 1; с) граф, в котором число ребер не меньше, чем число вершин, m  n, содержит цикл.

БИЛЕТ 3