6. Связь между координатным и естественным способами задания движения м.Т.

Координатный способ

С неподвижным центром О связывается неподвижная система координат ОХ у Z. Положение точки определяется тремя координатами: х, у, z . В процессе движения эти координаты изменяются, т.е. они являются функциями времени.

Зависимости

х=f₁(t);        у=f₂(t);        z=f₃(t)          

называются уравнениями движения точки в координатной форме. Эти уравнения являются одновременно параметрическими уравнениями траектории движения (параметром является t).

Чтобы получить уравнение траектории в явной форме, надо из уравнений исключить параметр t.

Естественный способ

При естественном способе задания движения траектория заранее известна. На траектории выбирается начало отсчета (т. 0) и устанавливается положительное и отрицательное направления отсчета.

Положение точки на траектории однозначно определяется криволинейной координатой S, измеряемой вдоль траектории.

Зависимость

S = f(t) (1.3)

называется уравнением движения в естественной форме.

Переход от координатного способа к естественному:

здесь:  ;              

7.Определение скорости и ускорения при векторном способе задания движения м.т.

Скорость точки при векторном способе задания движения.

П усть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:

(1)

На рис. 59 изображено как определяется скорость точки. За приращение времени Δt точка переместилась по траектории из положения M в положение M1, а радиус-вектор получил приращение Δr. Когда Δt 0, точка M1 M, а вектор Δr, направленный по хорде MM1, стремится занять положение касательной к траектории. Поэтому вектор скорости V будет направлен, согласно выражению (1), вдоль касательной к траектории в точке M в сторону движения точки.

По определению, вектор скорости является скоростью точки в данное мгновение времени или мгновенной скоростью. Средней скоростью за промежуток времени Δt называется отношение Δr/Δt. Размерность скорости - м/с (метр в секунду), внесистемными единицами скорости могут быть см/с (сантиметр в секунду), км/час (километр в час) и т.д.

Ускорение точки при векторном способе задания движения.

По определению ускорение является производной по времени от вектора скорости:

(2)

Когда Δ 0, точка M1 M; плоскость, где лежат векторы (t), (t + Δt) и (Δt), содержащая две касательные к траектории в точках M и M1 (рис. 62), стремится занять положение с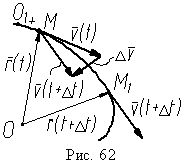 оприкасающейся плоскости в точке M; сам вектор направлен в сторону вогнутости траектории.

Таким образом, вектор ускорения a лежит в соприкасающейся плоскости и всегда направлен в сторону вогнутости траектории.

Очевидно, что a является ускорением в данное мгновение времени или мгновенным ускорением, а средним ускорением за промежуток времени Δt называется отношение ΔV / Δt. Соответственно, размерностью ускорения будет м / с2 (ме тр за секунду в квадрате).

8. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение движения, угловая скорость и угловое ускорение т.т.

Движение тела с двумя неподвижными точками (вращение тела вокруг неподвижной оси).

При вращении тела вокруг неподвижной оси две его точки, например A и B, лежащие на оси вращения, остаются неподвижными (рис 72, a).

Так как точки A и B кинематической модели неподвижны, то движение одной ее подвижной точки C определяет движение всех точек твердого тела, вращающегося вокруг неподвижной оси.

В частности (рис. 72, a), мы видим, что точка C движется по окружности радиуса OC = R, который называется радиусом вращения, в плоскости, перпендикулярной оси вращения. Следовательно, траекториями всех точек тела, не лежащих на оси вращения, являются окружности соответствующих радиусов, которые лежат в плоскостях, перпендикулярных оси вращения.

Кроме того, положение всех точек тела определяется тремя координатами точки C. Но эти три параметра связаны между собой двумя уравнениями постоянства длины отрезков AC и BC. То есть среди параметров только один независимый. Следовательно, твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы, которую в кинематике твердого тела называют вращательной или угловой степенью свободы.

Задание движения, кинематическое уравнение движения.

Для задания движения тела определим положение точки C в системе координат Oxyz, принятой за неподвижную, у которой ось Oz направлена по неподвижной оси вращения (рис. 72, b).

С телом свяжем систему координат Ox1y1z1, направляя ось Oz1 по оси вращения, а ось em>Ox1 так, чтобы она проходила по радиусу вращения через точку C. Тогда положение точки C можно определить радиусом вращения R и углом поворота φ связанной системы координат в неподвижной. Очевидно (рис. 72, b), что это угол поворота плоскости em>Ox1y1 и треугольника ABC, вращающихся вместе с телом вокруг оси Oz и стороны AB.

Так как R = const, то положение точки C, а следовательно, и всего тела, определяется одним переменным параметром φ, изменяющимся с течением времени при движении тела. Записав это математически, получим кинематическое уравнение движения твердого тела с двумя неподвижными точками:

φ = φ(t) (4)

Отметим, что угол φ измеряется в плоскости, перпендикулярной оси вращения (на рис. 72, b - в плоскости xOy). Единицей измерения угла является радиан, внесистемными единицами могут быть градус, оборот и т.д. Дуговая стрелка с обозначением φ показывает направление увеличения угла (на рис. 72, b принято, что угол увеличивается против хода часов, смотря с конца оси Oz, совпадающей с осью вращения).

Угловая скорость и угловое ускорение.

Здесь мы рассмотрим новые кинематические параметры, характеризующие движение твердого тела в целом.

Угловой скоростью называется кинематический параметр, характеризующий быстроту изменения угла поворота твердого тела с течением времени.

По определению угловая скорость является производной по времени от угла поворота:

(5)

Эта производная содержит информацию о величине угловой скорости и направлении вращения. Величина угловой скорости равна

(6)

Направление вращения определяет знак производной. Если φ' > 0, то угол поворота φ увеличивается, вращение происходит в сторону увеличения угла поворота. Если φ' < 0, угол уменьшается, вращение направлено в сторону уменьшения угла поворота. Направление вращения указывается дуговой стрелкой с обозначением w. На рис. 72, b направление вращения показано для случая, когда φ' > 0.

Угловая скорость, найденная по формуле (5), является мгновенной угловой скоростью в момент времени t. Отношение называется средней угловой скоростью за промежуток времени . Поэтому размерностью угловой скорости будет радиан в секунду, внесистемными единицами могут быть градус в секунду, оборот в минуту и т.д.

Угловым ускорением называется кинематический параметр, характеризующий быстроту изменения угловой скорости с течением времени:

(7)

Величина углового ускорения равна

(8)

Сравнивая знаки производных φ' и φ'', можно определить является ли вращение ускоренным или замедленным. Когда производные имеют одинаковые знаки (положительные или отрицательные), угловая скорость возрастает, вращение является ускоренным; когда их знаки разные, угловая скорость уменьшается, вращение будет замедленным. Направление углового ускорения указывается дуговой стрелкой с обозначением ε. При ускоренном вращении угловое ускорение совпадает с направлением вращения, а при замедленном вращении угловое ускорение направлено противоположно вращению. На рис. 72, b показано замедленное вращение, когда φ' > 0, а φ'' < 0.

Угловое ускорение в формуле (7) является мгновенным угловым ускорением в момент времени t. Отношение Δw / Δt называется средним угловым ускорением за промежуток времени Δt. Размерностью углового ускорения будет радиан за секунду в квадрате, внесистемными единицами могут быть градус за секунду в квадрате и т.

9. Скорость и ускорение точки вращающегося тела вокруг неподвижной оси (формулы и рисунок).

В этом случае для определения скоростей и ускорений всех точек тела нам нужно найти скорость и ускорение только одной точки тела.

Д ля этого на рис. 73 покажем вид сверху на рис. 72, b и перейдем к естественному способу задания движения точки C тела. Начало отсчета будет в точке пересечения O1 окружности радиуса R с осью Ox, от которой отсчитывается угол поворота φ , а положительное направление отсчета дуговой координаты будет направлено в сторону увеличения угла поворота. Тогда положение точки C тела на ее траектории (окружности) определяется дуговой координатой s = RΔ , а скорость и ускорение точки выражаются в виде

(9)

(10)

Согласно формулам (9) и (10), величины этих векторов равны

(11)

(12)

(13)

Так как касательная к окружности перпендикулярна ее радиусу, единичный вектор τR, а единичный вектор n направлен по радиусу вращения к оси вращения от точки C к точке O. Следовательно, вектор an будет также направлен по радиусу вращения к оси вращения s'2 / R = R φ'2 > 0 . Векторы V и aτ будут перпендикулярны радиусу вращения:

(14)

Вектор V направлен в сторону вращения, которую указывает стрелка угловой скорости, а вектор aτ - в сторону стрелки углового ускорения, так как знаки производных от угла поворота определяют знаки производных дуговой координаты (R > 0) . На рис. 73 изображен случай замедленного вращения, когда φ' > 0, φ'' < 0, и соответственно, s' > 0, s'' < 0.

Итак:

1. Величина вектора скорости любой точки твердого тела, вращающегося вокруг неподвижной оси, равна произведению величины угловой скорости тела на радиус вращения точки; вектор скорости перпендикулярен радиусу вращения и направлен в сторону вращения.

2. Величина вектора касательного ускорения равна произведению величины углового ускорения на радиус вращения; вектор касательного ускорения перпендикулярен радиусу вращения и направлен в сторону стрелки углового ускорения.

3. Величина вектора нормального ускорения равна произведению квадрата величины угловой скорости на радиус вращения; вектор нормального ускорения направлен по радиусу вращения всегда от точки к оси вращения.

Величина вектора ускорения точки, которое часто называют полным ускорением, равна

(15)

Вектор полного ускорения отклонен от радиуса вращения на угол β, который определяется из формулы

9. Поступательное движение т.т. Теорема о скоростях и ускорения точек т.т.

При поступательном движении любая прямая, проведенная в твердом теле, движется параллельно самой себе.

На рис. 71 изображено тело в момент времени t. Положение трех его точек A, B, C в системе отсчета определяется тремя радиус-векторами rA, rB и rC. За время Δt тело переместится, и точки займут новые положения A', B', C'. Так как при поступательном движении стороны треугольника ABC двигаются параллельно самим себе, то A'B' // AB, B'C' // BC и A'C' // AC. Поэтому приращения радиус-векторов или элементарные перемещения трех точек твердого тела, а следовательно, и всех его точек, будут равны между собой как стороны параллелограммов, то есть

(1)

Это может быть только тогда, когда траектории точек тела являются одинаковыми кривыми. Вспомнив формулу нахождения скорости

мы видим из выражения (1), что скорости трех точек, а следовательно, и всех точек твердого тела, одинаковы, то есть

(2)

Дифференцируя по времени выражение (2) мы докажем, что одинаковы и ускорения всех точек тела:

(3)

Таким образом, при поступательном движении твердого тела одинаковы траектории, скорости и ускорения всех его точек.

Поэтому твердое тело в поступательном движении можно принять за материальную точку и использовать при исследовании движения твердого тела законы кинематики точки. В частности, твердое тело в поступательном движении имеет столько же степеней свободы, как и материальная точка. Если материальная точка свободная, то тело, которое принято за точку, имеет три степени свободы, которые в кинематике твердого тела называются поступательными степенями свободы.

9. Сложное движение м.т. Относительное, переносное и абсолютное движения м.т. Теорема о сложении скоростей – определение абсолютной скорости точки.

Основные понятия и определения.

Р ассмотрим простейший случай, когда движение точки исследуется в двух системах координат, одну из которых Oxyz мы примем за неподвижную, а вторую - Ax1y1z1 считаем подвижной (рис. 104).

Движение точки относительно неподвижной системы координат называется абсолютным движением точки.

Движение точки относительно подвижной системы координат называется относительным движением точки. Все параметры относительного движения точки пишутся с подстрочным индексом r (от латинского relativus - относительный), например, относительная скорость точки - r.

Движение подвижной системы координат в неподвижной системе координат называется переносным движением.

Для выделения переносного движения точки используют прием остановки или замораживания. Точку мысленно останавливают в подвижной системе координат (вмораживают в подвижную систему координат) и наблюдают, как подвижная система координат переносит точку относительно неподвижной системы координат. Это и будет переносным движением точки.

Все параметры переносного движения и переносного движения точки пишутся с подстрочным индексом e (от латинского entraner - увлекать за собой), например, угловая скорость вращения подвижной системы координат в неподвижной - ωe, или переносная скорость точки - e.

Прием останова можно использовать и для выделения относительного движения точки, мысленно останавливая переносное движение подвижной системы координат в неподвижной.

Теоремы о сложении скоростей точки и об абсолютной производной вектора.

З десь мы рассмотрим как вычисляется абсолютная скорость точки, участвующей в сложном движении, доказав при этом теорему об абсолютной производной вектора.

Положение точки M и начала подвижной системы координат точки A в неподвижной системе координат определим радиус-векторами r и rA, положение точки M в подвижной системе координат определим радиус-вектором ρ, который известен в проекциях на оси подвижной системы координат, т.е. ρ = x1i1 + y1j1 + z1k1. На рис. 105 мы видим, что r = rA + ρ. Аналогичное выражение было получено и для движения свободного твердого тела. Однако в нашем случае точка M свободно перемещается в подвижной системе координат, ее радиус-вектор изменяется не только по направлению, но и по величине: ρ < > const.

Дифференцируя по времени выражение r находим абсолютную скорость точки, которая характеризует быстроту изменения положения точки в неподвижной системе координат:

(1)

где A - абсолютная скорость начала подвижной системы координат; dρ / dt является производной вектора ρ, известного в подвижной системе координат, которую находят в неподвижной системе координат и называют абсолютной производной вектора ρ.

Найдем абсолютную производную вектора ρ:

(2)

Учитывая, что единичные векторы подвижной системы координат изменяют свое направление в пространстве, но постоянны по величине, используем формулу Эйлера для вычисления их производных, согласно которой

где ω - угловая скорость вращения подвижной системы координат в неподвижной. Поэтому сумма последних трех слагаемых в (2) равна

(3)

Первые три слагаемых в (2) характеризуют быстроту изменения вектора ρ в подвижной системе координат и их сумма называется относительной или локальной производной:

(4)

Подставляя выражения (3) и (4) в (2), получаем

(5)

Заметим, что если ρ = const, из (4) следует равенство нулю относительной производной вектора ρ, а из (5) получается формула Эйлера.

То есть мы показали справедливость формулы Эйлера и для векторов постоянных по величине, известных в произвольно двигающихся системах координат, так как здесь на движение подвижной системы координат никакие ограничения не накладывались.

Выражение (5) можно распространить и на любой другой вектор, известный в подвижной системе координат, например, b :

(6)

9. Сложное движение м.т. Теорема о сложении ускорений – определение абсолютного ускорения м.т.

Р ассмотрим простейший случай, когда движение точки исследуется в двух системах координат, одну из которых Oxyz мы примем за неподвижную, а вторую - Ax1y1z1 считаем подвижной (рис. 104).

Движение точки относительно неподвижной системы координат называется абсолютным движением точки.

Движение точки относительно подвижной системы координат называется относительным движением точки. Все параметры относительного движения точки пишутся с подстрочным индексом r (от латинского relativus - относительный), например, относительная скорость точки - r.

Движение подвижной системы координат в неподвижной системе координат называется переносным движением.

Для выделения переносного движения точки используют прием остановки или замораживания. Точку мысленно останавливают в подвижной системе координат (вмораживают в подвижную систему координат) и наблюдают, как подвижная система координат переносит точку относительно неподвижной системы координат. Это и будет переносным движением точки.

Все параметры переносного движения и переносного движения точки пишутся с подстрочным индексом e (от латинского entraner - увлекать за собой), например, угловая скорость вращения подвижной системы координат в неподвижной - ωe, или переносная скорость точки - e.

Прием останова можно использовать и для выделения относительного движения точки, мысленно останавливая переносное движение подвижной системы координат в неподвижной.

Теорема о сложении ускорений (теорема Кориолиса).

Дифференцируя это выражение по времени получаем,

(11)

В выражении (11) V' = aA является ускорением начала подвижной системы координат; ωe = εe является угловым ускорением переносного движения или угловым ускорением вращения подвижной системы координат в неподвижной. Векторы Vr и ρ известны в проекциях на оси подвижной системы координат и изменяются по величине и направлению, поэтому, согласно теореме об абсолютной производной вектора,

(12)

В выражениях (12) локальная производная вектора скорости характеризует быстроту его изменения в подвижной системе координат и является относительным ускорением. Таким образом, из (11) имеем

(13)

Для выделения переносного ускорения используем прием останова, принимая в (13) ar = 0 и Vr = 0. Когда точка остановлена в подвижной системе координат (вморожена в подвижную систему координат), она за счет движения подвижной системы координат переносится относительно неподвижной, и ее абсолютное ускорение равно переносному ускорению a = ae. Учитывая это, из (13) получаем

(14)

то есть переносное ускорение совпадает с ускорением той точки подвижной системы координат, где в данное мгновение времени находится материальная точка, если принять подвижную систему координат за твердое тело. Картина движения будет нагляднее, если подвижный трехгранник Ox1y1z1 на рис. 105 принять за ледяной трехгранник, где в данный момент времени, в данном положении вморожена точка M.

Подставляя выражение (14) в (13), имеем

(15)

Последнее слагаемое в (15) называется кориолисовым ускорением и обозначается ac. Таким образом, имеем математическую запись теоремы:

(16)

которую можно сформулировать так: абсолютное ускорение точки, участвующей в сложном движении, равно геометрической сумме относительного, переносного и кориолисова ускорений.

Остановимся на кориолисовом ускорении, равном

(17)

Величина кориолисова ускорения вычисляется по формуле

(18)

а направление вектора определяется по правилу построения вектора векторного произведения векторов ωe и Vr (рис. 106, a). Когда переносное и относительное движение лежат в одной плоскости, построение вектора кориолисова ускорения облегчается применением правила Н.Е. Жуковского. В этом случае для нахождения направления кориолисова ускорения достаточно повернуть вектор относительной скорости на угол 90° в сторону переносного вращения (рис. 106, b).

На основании формулы (18) можно указать следующие случаи, когда кориолисово ускорение равно нулю: 1) ωe = 0; 2) ωe//Vr; 3) Vr = 0. Второй и третий случаи могут возникать в процессе движения, но особого интереса не представляют. Первый случай имеет место, когда переносное движение поступательное, и часто встречается при решении конкретных вопросов теории и практических задач.

№13

-------- Кориолисово ускорение.

Поворотным ускорением (ускорением Кориолиса) называется соста­вляющая абсолютного ускорения точки в составном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относитель­ную скорость точки:

Появление поворотного ускорения обусло­вливается двумя причинами:

1) вследствие относительного движения точки, перемещающейся по отношению к под­вижной системе отсчета, изменяется перенос­ная скорость точки; 2) вследствие вращательного переносного движения дополнительно изменяется направление относительной скорости по отношению к не­подвижной системе отсчета.

Например, если человек идет равномерно вдоль радиуса равно­мерно вращающейся платформы, то его относительной скоростью является скорость его движения вдоль радиуса, а пе­реносной— скорость той точки платформы, где он на­ходится в данный момент.

------------- Определение модуля и направления(Правило Жуковского)

Модуль поворотного ускорения определяется как модуль векторного произведения:

Для определения направления поворотного уско­рения удобно пользоваться правилом Жуковского:

Чтобы найти направление поворотного ускорения, следует спроектировать относи­тельную скорость точки на плоскость, перпен­дикулярную оси переносного вращения, и повер­нуть эту проекцию в той же плоскости на 90°, в сторону переносного вращения

№14-15

----------- ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ т.т.

Плоскопараллельным или плоским называют движение твердого тела, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Плоское движение тел является одним из наиболее распространенных в технике. Плоское движение совершают тела качения ( колеса, катки, цилиндры ) на прямолинейном участке пути; отдельные детали механизмов, предназначенных для преобразования вращательного движения одного тела в поступательное или колебательное другого; шестерни планетарных передач.

В теории плоского движения тел доказывается несколько предложений.

1. Для описания плоского движения тел достаточно описать движение точек одного сечения тела плоскостью, параллельной неподвижной плоскости.

2. Движение тела может рассматриваться как результат сложения поступательного движения и вращения тела относительно одной из точек тела, называемой полюсом.

3. Характеристики вращательного движения тела при его плоском движении не зависят от выбора полюса.

------------ Теорема о сложении скоростей

Связь между относитель­ной, переносной и абсолютной скоростями точки устанавливается сле­дующей теоремой.

Теорема. Абсолютная скорость точки равна сумме переносной и от­носительной скоростей:

------------------ Теорема о сложении ускорений (теорема Кориоли­са)

Абсолютное ускорение точки равно сумме переносного, от­носительного и кориолисова ускорений:

Можно сказать, что часть абсолютного ускорения — ускорение Ко­риолиса — связана с изменением абсолютной скорости, обусловленным двумя причинами: 1) влиянием переносного движения на относитель­ную скорость; 2) влиянием относительного движения на переносную ско­рость

------------- Теорема о проекциях скоростей 2-х точек тела.

Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.

Теорема позволяет легко находить скорость данной точки тела, если известны направление скорости этой точки и ско­рость какой-нибудь другой точки того же тела.

Аналитический способ определения скоростей точек тела

При использовании аналитического метода считаются известными уравнения движения плоской фигуры (тела, совершающего плоскопараллельное движение):               (1)   Тогда координаты точки М (рис.) будут (2) где b – расстояние от точки М до полюса А.

Модуль скорости точки М определяется по формуле

.

    Направление вектора V_м определяется по направляющим косинусам:

    Таким образом, задача по определению скоростей точек плоской фигуры сводится к известному решению соответствующей задачи кинематики точки.

    Угловая скорость плоской фигуры определяется дифференцированием последнего уравнения из (1), т.е.

         (3)                                                                 

    Аналитический метод решения задачи рекомендуется использовать в тех случаях, когда требуется определить скорости точек для большого числа положений плоской фигуры.

Аналитический способ определения ускорений точек тела

П ри использовании аналитического метода уравнения движения (1) плоской фигуры считаются известными. Дважды дифференцируя по времени выражения (2) координат точки М, получим проекции ускорения этой точки:

   Модуль ускорения равен

.

    Направление ускорения определяется направляющими косинусами:

.

    Таким образом, задача по определению ускорений точек сводится к соответствующей задаче кинематики точки.

    Угловое ускорение тела находится дифференцированием третьего уравнения движения из (1)

№16-17

------------- ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ т.т. МЦС

Мгновенный центр скоростей (М.Ц.С. и обозначают буквой Р) — точка, обладающая следующими свойствами: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело.

Доказательство следующее. Векторы скоростей точек плоскости, связанной с фигурой, определяются векторной суммой двух векторов, один из которых одинаков для всех точек плоскости, а другой зависит от положения точки на плоскости. Значит, на плоскости должна существовать точка, где вектор скорости во вращении относительно полюса равен по величине, но направлен противоположно вектору скорости полюса. Эта точка и будет иметь скорость, равную нулю, т.е. являться мгновенным центром скоростей.

------------Определение угловой скорости тела скоростей точек тела.

Скорость любой точки тела при плоском движении равна геометрической сумме скорости полюса и скорости во вращении точки относительно полюса.

------------ Общий случай нахождения МЦС--??????

1. При выборе в качестве полюса мгновенного центра скоростей величины и направления скоростей точек тела при его плоском движении определяются точно так же, как и при вращательном. Отличием является то, что для каждого момента движения тела положение мгновенной оси вращения необходимо находить. Соответственно необходимо находить и расстояния точек до этой оси.

2. Скорости всех точек фигуры при ее плоском движении пропорциональны их расстояниям до М.Ц.С. и перпендикулярны радиусам вращения - т.е. отрезкам, соединяющим точки с М.Ц.С.

3. Если уметь определять положение мгновенных центров скоростей звеньев плоских механизмов, то задачи на определение скоростей точек и угловых скоростей звеньев этих механизмов окажутся ничуть не сложнее аналогичных задач на вращательное движение связанных между собой тел.

----------Различные способы нахождения МЦС