Лабораторная работа №4

Предсказание и оценивание величин с использованием метода регрессионного анализа в среде ms Excel

Цель работы: Получить навыки построения уравнения регрессии в среде электронных таблиц MS Excel.

Задачи работы: Изучить метод регрессионного анализа и возможности применения его при решении экономических задач. Изучить основные статистические функции, позволяющие рассчитывать параметры регрессионной модели при помощи электронных таблиц MS Excel. На основе экспериментальных данных построить математическую модель (уравнение регрессии), описывающую поведение некоторой характеристики в зависимости от изменения множества факторов. Сделать выводы.

Теоретические сведения

Регрессионный анализ является одним из наиболее широко используемых статистических методов, однако, в тоже время, часто является причиной ошибочных выводов. Это связано с тем, что регрессионный анализ – довольно длинная технологическая цепочка обработки данных. С одной стороны в нем задействовано множество других статистических методов (корреляционный анализ, дисперсионный анализ), с другой стороны – используются методы линейной алгебры. Такая сложность вызывает ряд взаимосвязанных проблем в применении регрессионного анализа. Поэтому, проведение полного регрессионного анализа с помощью электронных таблиц MS Excel не представляется возможным. В данной работе будут рассмотрены элементы регрессионного анализа, в частности, методика построения уравнения регрессии по опытным данным и оценка качества модели.

Предсказание (или прогнозирование) одной величины по оценке другой предполагает получение информации относительно оценки и закона поведения одной величины по характеристике другой, когда между ними установлена какая-либо связь. В экономике задача предсказания или прогнозирования является одной из центральных. Прогноз котировки валют, предсказание поведения конкурентов, оценка влияния изменения уровня инфляции и других рыночных факторов на прибыль предприятия, оценка изменения спроса и выявления доминирующих факторов и т.д. – все это задачи, которые могут решаться с использованием метода регрессионного анализа.

Чтобы вывести способ оценивания объекта по одной переменной, например , на основе другой переменной, например , прежде всего, необходимо определить связь между этими величинами. Переменная, которая оценивается ( ), называется зависимой переменной или откликом, а переменная, используемая для оценки ( ) – независимой переменной или фактором. Предположим, что мы нашли уравнение для предсказания по , которое обладает удовлетворительными свойствами. Такое уравнение называется уравнением регрессии или линией регрессии. Уравнение это определяется двумя константами и , т.е. эти константы определяют оцениваемую величину как

. (4.1)

Величина является предсказанным значением для -го объекта. Очевидно, что не всегда будет равно , т.е. даже при наилучшем линейном уравнении предсказания, как правило, будет иметь место ошибка. Тогда величина будет равна:

,

где - ошибка оценки по для -го объекта:

.

Коэффициенты и должны выбираться так, чтобы сумма квадратов ошибки оценки была минимальная, т.е.:

.

Этот критерий для определения и называется критерием наименьших квадратов, а метод, позволяющий получать коэффициенты уравнения регрессии, называется методом наименьших квадратов. Выбор такого критерия является в некоторой степени произвольным. Он обусловлен исторически и удобен с вычислительной точки зрения.

Коэффициент или , называется выборочным коэффициентом регрессии (поскольку определяется на основе несгруппированных выборочных данных) и определяется следующим выражением:

а задается уравнением:

Ошибка оценки для -го объекта определяется как:

На рис. 4.1 показана прямая линия регрессии и ошибка оценки, для примера, приведенного в лабораторной работе №3 в таблице 3.1.

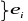
Рис. 4.1 Прямая линии регрессии

Средняя ошибка оценки всегда равна 0:

Для оценки точности предсказания используется показатель дисперсии ошибки оценки, которая рассчитывается следующим образом:

.

Положительное значение квадратного корня из дисперсии ошибки является среднеквадратической стандартной ошибкой:

. (4.2)

Стандартную ошибку оценки можно применить для определения пределов в окрестности предсказанного значения , в которые, вероятно, попадает фактическое значение для объекта.

Стандартная ошибка предсказанного значения для отдельного , приведенного в таблице 1, равна: .

Если исследуется связь между несколькими признаками, то корреляцию называют множественной.

В простейшем случае число признаков равно трем и связь между ними линейная:

. (4.3)

В этом случае возникают задачи:

1. найти по данным наблюдений выборочное уравнение связи вида: ;

2. оценить тесноту связи между и обоими признаками , ;

3. оценить тесноту связи между и (при постоянном ), между и ( при постоянном ).

Первая задача решается методом наименьших квадратов, причем уравнение регрессии удобно искать в виде:

,

где

;

.

Здесь - коэффициенты корреляции между соответствующими признаками; - средние квадратичные отклонения.

Возможно определить связь и между большим количеством переменных, а также построить уравнение множественной регрессии.

Теснота связи признака с признаками оценивается множественным коэффициентом корреляции, который рассчитывается следующим образом:

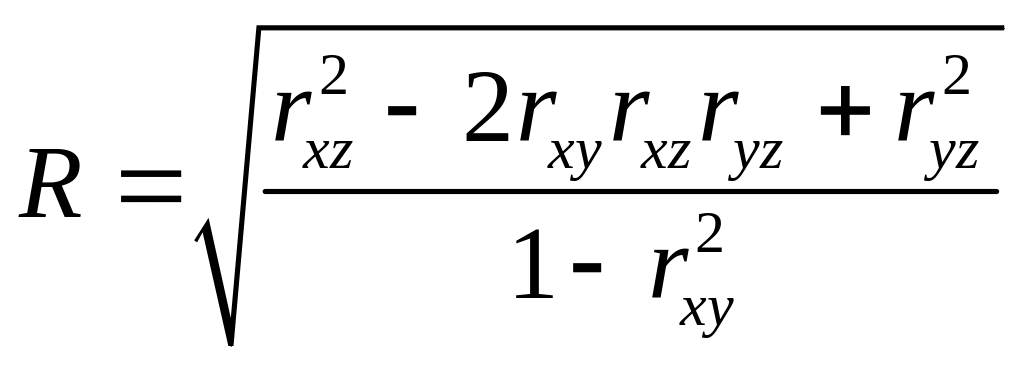_{, (4.4)}

причем R измеряется в пределах от 0 до 1.

В MS Excel для расчета коэффициентов линейного уравнения регрессии используется следующая функция:

ЛИНЕЙН – Позволяет подобрать по имеющимся исходным данным линию регрессии или линейное уравнение множественной регрессии, рассчитать его коэффициенты и некоторые другие дополнительные статистические показатели. Уравнение для прямой линии имеет вид (4.1) или (4.3), коэффициенты которого вычисляются по описанному выше методу наименьших квадратов.

Полученные результаты данная функция возвращает в виде массива, поэтому она должна вводиться как формула массива. Для ее ввода необходимо выделить диапазон ячеек, в которые будут выводиться результаты, после чего ввести формулу и нажать комбинацию клавиш [Ctrl]+[Shift]+[Enter]. MS Excel автоматически заключит введенную формулу в фигурные скобки {ЛИНЕЙН()}.

Синтаксис

ЛИНЕЙН(известные_значения_y;[известные_значения_x];[конст]; [статистика])

Известные_значения_y    — множество значений зависимой переменной (результативного признака, отклика). Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная. Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.

Известные_значения_x    — множество значений независимой переменной (объясняющей переменной, фактора, факторного признака). Данный аргумент является необязательным, поэтому и заключен в квадратные скобки. Массив известные_значения_x может состоять из одного или нескольких множеств переменных. Если используется только одна переменная, то аргумент известные_значения_y и известные_значения_x могут быть диапазонами любой формы, но обязательно иметь одинаковую размерность (количество значений должно соответствовать количеству значений ). Если используется более одной переменной, то аргумент известные_значения_y должен быть диапазоном ячеек в виде одной строки или в виде одного столбца (вектор значений).Если аргумент известные_значения_x опущены, то предполагается, что это массив {1;2;3;...} такого же размера, как и известные_значения_y.

Конст    — необязательное логическое значение, которое указывает, требуется ли, чтобы свободный член получаемого уравнения регрессии был равен 0. Если аргумент конст имеет значение ИСТИНА или опущено, то вычисляется обычным образом.В противном случае, полагается равным 0 и подбирается таким образом, чтобы выполнялось соотношение .

Статистика    — логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительные статистические показатели полученного уравнения регрессии. Данные показатели будут рассмотрены позднее при анализе качества модели. Если аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН возвращает только коэффициенты и постоянную .

Если имеет только одна независимая переменная , то значения коэффициента при уравнения регрессии и свободного члена (координата пересечении линии регрессии с осью координат) можно получить непосредственно, используя формулы:

: ИНДЕКС(ЛИНЕЙН(неизвестные_значения_y, неизвестные_значения_х); 1);

: ИНДЕКС(ЛИНЕЙН(неизвестные_значения_y, неизвестные_значения_х); 2).

Для вычисления ошибки полученного уравнения регрессии используется следующая функция:

СТОШYX - возвращает стандартную ошибку предсказанных значений для каждого значения в регрессии.

Синтаксис

СТОШYX(известные_значения_y;известные_значения_x)

Известные_значения_y   - это массив или интервал зависимых точек данных.

Известные_значения_x   - это массив или интервал независимых точек данных.

Если график регрессии изображается кривой линией, то корреляцию называют криволинейной.

Например, функции регрессии на могут иметь вид:

(параболическая корреляция второго порядка);

(параболическая корреляция третьего порядка).

Для определения функции регрессии строят точки и по их расположению делают заключение о примерном виде функции регрессии; при окончательном решении принимают во внимание особенности, вытекающие из сущности решаемой задачи.

Теория линейной корреляции решает те же задачи, что и теория линейной корреляции (установление формы и тесноты корреляционной связи). Неизвестные параметры уравнения регрессии ищут методом наименьших квадратов.

Пусть имеется наблюдений (выборки), между признаками которых существует некоторая корреляционная связь. Пусть выборочное уравнение регрессии на имеет вид:

,

где - неизвестные параметры.

Пользуясь методом наименьших квадратов получают систему линейных уравнений относительно неизвестных параметров:

Найденные из системы параметры подставляют в выборочное уравнение регрессии. На рис. 4.2 приведен пример криволинейной линии регрессии.

Рис.4.2 - Пример криволинейной линии регрессии

Для получения коэффициентов криволинейной линии регрессии, в частности показательного (экспоненциального) уравнения множественного регрессии, в MS Excel предусмотрена функция ЛГРФПРИБЛ. Назначение и синтаксис данной функции следующие:

ЛГРФПРИБЛ – позволяет подобрать по имеющимся исходным данным показательное уравнение множественной регрессии, рассчитаеть его коэффициенты и некоторые другие дополнительные статистики. Полученные результаты данная функция возвращает в виде массива.

Уравнение регрессии, подбираемое посредством данной функции имеет вид:

_,

где - теоретические (рассчитанные по полученному уравнению регрессии) значения результирующего признака (отклика, зависимой переменной) , - значения объясняющих независимых -х переменных (факторов); - коэффициенты уравнения регрессии.

Синтаксис

ЛГРФПРИБЛ(известные_значения_y; [известные_значения_x]; [конст]; [статистика])

Известные_значения_y    — множество значений зависимой переменной .

Известные_значения_x    — необязательное множество значений независимой переменной .

Описание остальных аргументов данной функции аналогично описанию аргументов функции ЛИНЕЙН.

Для расчета величины , которая является предсказанным значением для -го объекта, с целью управления процедуры вычисления, можно воспользоваться функцией ТЕНДЕНЦИЯ.

ТЕНДЕНЦИЯ – вычисляет и возвращает массив прогнозных значений зависимой переменной , соответствующих заданным значениям на основе уравнения линейной регрессии, которое подбирается этой же функцией с использованием имеющихся значений зависимой и независимой переменной. Функция возвращает результат в виде массива. Работа с данной функцией аналогична работе с функциями ЛИНЕЙН и ЛГРФПРИБЛ.

Синтаксис

ТЕНДЕНЦИЯ(известные_значения_y; [известные_значения_x]; [новые_значения_x]; [конст])

Известные_значения_y    — множество значений зависимой переменной .

Известные_значения_x    — необязательное множество значений независимой переменной .

Новые_значения_x    — новые значения , для которых ТЕНДЕНЦИЯ возвращает соответствующие значения .

Свойства и назначение аргументов аналогичны функции ЛИНЕЙН.

Замечания

• Можно использовать функцию ТЕНДЕНЦИЯ для аппроксимации полиномиальной кривой, проводя регрессионный анализ для той же переменной, возведенной в различные степени. Например, пусть столбец A содержит значения , а столбец B содержит значения . Можно ввести в столбец C, в столбец D, и так далее, а затем провести регрессионный анализ столбцов от B до D со столбцом A.

• Формулы, которые возвращают массивы, должны быть введены как формулы массива.

• При вводе константы массива для аргумента, такого как известные_значения_x, следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк.

Пусть необходимо оценить зависимость между величиной резервного фонда предприятия и множеством рыночных факторов, таких как:

- уровень инфляции, %;

- объем промышленного производства в области, млн. грн.;

- изменение процента налогообложения чистой прибыли, %;

- объемы продаж, тыс. грн..

Исходные данные представлены в таблице 4.1.

Рассчитаем для данных, приведенных в таблице 4.1, коэффициенты уравнений линейной и показательной регрессий, определим стандартную ошибку и вычислим ряд прогнозных значений величины резервного фонда. На рис. 4.3 приведена копия экрана с результатами расчетов. На рис. 4.4 показаны расчетные формулы. Следует не забывать, что функции ЛИНЕЙН, ЛГРФПРИБЛ и ТЕНДЕНЦИЯ вводятся как массивы (рис. 4.5).

Таблица 4.1

Отчетные данные по рыночным показателям за период 1999 – 2000 гг.

Период	f1	f2	f3	f4	Резервный фонд, Y
1	0,5	1,2	0,01	324,6	120,89
2	0,91	1,1	0,06	356,8	234,7
3	0,4	3,4	0,01	456,8	145,8
4	0,51	1,5	0,02	234,6	123,89
5	0,8	1,6	0,05	345,78	234,7
6	1,2	1,8	0,07	456,78	357,8
7	0,2	1,4	0,01	199,4	127,89
8	0,65	0,9	0,01	346,2	178,6
9	0,3	1,56	0,02	256,78	156,7
10	0,81	1,4	0,04	247,8	200,6
11	0,9	1,9	0,05	567,9	234,5
12	0,4	0,78	0,01	278,4	125,6
13	0,12	1,5	0,01	257,8	78,9
14	0,67	1,6	0,08	456,3	290,8
15	0,4	1,2	0,07	491,1	274,5
16	0,7	1,4	0,04	234,56	264,6
17	0,3	1,6	0,01	235,7	128,9
18	0,78	1,7	0,03	378,4	200,45
19	0,6	1,3	0,02	417,9	199,6
20	0,52	1,23	0,01	511,6	178,4

Рис. 4.3 - Исходные данные и результаты расчетов

Рис. 4.4 - Расчетные формулы для вычисления коэффициентов регрессии

Рис. 4.5 – Ввод массива

Для получения результата в виде массива функцию необходимо вводить в строке формул, а для заключения функции в фигурные скобки необходимо нажать [Ctrl]+[Shift]+[Enter].

Как видно из рис. 4.3, при определении зависимости между параметрами резервный фонд предприятия и уровень инфляции, получается следующее уравнение регрессии: Y=202,19*f1+74,91.

При оценке зависимости резервного фонда от множества всех факторов получается следующее уравнение: Y=82,89*f1-1,92*f2+1827,04*f3+0,08*f4+62,52.

Показательное уравнение регрессии будет следующим:

Y=88,07*1,69^f1*0,98^f2*3822,76^f3*1,00^f4.

Стандартная ошибка для каждого фактора соответственно будет иметь следующие значения: 45,28; 72,11; 33,00; 60,87.

Построение графика уравнения регрессии можно выполнить двумя способами.

Первый способ: при помощи функции ТЕНДЕНЦИЯ получить ряд предсказанных значений зависимой переменной , как показано на рис. 4.3. Далее с помощью Мастера функций построить линию регрессии (рис. 4. 6).

Рис. 4.6 – График уравнения регрессии, построенный первым способом

Второй способ: отобразить график рассеивания известных значений зависимой переменной и независимой переменной при помощи Мастера функций (рекомендуется выбрать тип графика - точечный) (рис. 4.7). С помощью указателя мыши выделить точки на графики и нажать правую клавишу мыши. Затем во всплывающем меню выбрать пункт Добавить линию тренда (рис. 4.8). В появившемся окне (рис. 4.9) выбрать желаемый тип линии и нажать кнопку ОК. На рис. 4.10 отображен результата построения. Также можно задать и другие параметры линии тренда. Такой способ более удобен, если важно наглядное отображение данных, а не точные результаты вычисления предсказанных значений.

Рис. 4.7 – Построение точечного графика функции по исходным данным

Рис. 4.8 – Добавление линии тренда

Рис. 4.9 – Выбор типа линии тренда

Рис. 4.10 - График уравнения регрессии, построенный вторым способом

Аналогичные результаты можно получить с помощью пакета Анализ данных. Для этого необходимо в меню Сервис выбрать соответствующий пункт и на экране появится окно выбора метода анализа (рис. 4.11). Выбрав пункт регрессия и нажав кнопку ОК, появится следующее окно, где необходимо задать параметры для проведения регрессионного анализа (рис. 4.12).

Рис. 4.11 – Окно выбора метода анализа

Рис.4.12 – Окно задания параметров

Для проведения регрессионного анализа необходимы следующие параметры:

Входной интервал Y – вводят ссылку на столбец средних значений отклика.

Входной интервал Х – вводят ссылку на матрицу регрессов.

Уровень надёжности – доверительная вероятность, которую используют при проверке всех статистических гипотез в регрессионном анализе.

Метки – выбирают в том случае, если, задавая ссылки на Х и Y, включают в ссылочную область и имена переменных.

Для вывода информации рекомендуем задать «Новый рабочий лист». Если предполагается выводить и графики, то при некоторых способах подключение пакета анализа необходимо задать «Новая рабочая книга».

Для дальнейшего анализа следует запросить (отметить): «Остатки», «Стандартизированные остатки», «График остатков», «График подбора». В данной работе эти параметры, за исключением «Графика подбора», анализироваться не будут.

Программа выводит четыре таблицы: «Регрессионная статистика», «Дисперсионный анализ», «Вывод остатка», таблицу коэффициентов регрессии и их статистических характеристик. На рис. 4.13 показаны результаты работы программы Регрессия.

Рис. 4.13 – Результат работы программы Регрессия

Как видно из рис. 4.13, в ячейках В17:В21 расположены коэффициенты линейного уравнения регрессии, которые полностью соответствуют тем, которые получены с помощью функции ЛИНЕЙН. Также изображен график подбора для первого фактора, который также практически идентичен с построенной другим способом линией регрессии. Все остальные данные, изображенные на рис. 4.13, необходимы для дальнейшего анализа качества построенной модели и в данной работе не рассматриваются.

Таким образом, с помощью встроенных функций MS Excel, а также пакета Анализ данных можно оперативно и качественно построить уравнение регрессии для анализа любых экономических данных.