Лабораторная работа № 3 приближенное вычисление определенных интегралов. Методы прямоугольников, трапеций и симпсона

Цель работы – научиться численно интегрировать и оценивать погрешность вычислений. Найти приближенное значение определенного интеграла

,

где f(х) – непрерывная функция на отрезке [а, b], с помощью методов левых, правых, средних прямоугольников, трапеций и Симпсона. Оценить априорную и апостериорную погрешности полученных результатов.

Постановка задачи

1. Изучить теоретические сведения.

2. Выполнить ручной счёт для вычисления приближенного значения интеграла , используя квадратурные формулы правых, левых, средних прямоугольников, формулы трапеций и Симпсона. Принять n = 12, где n – количество интервалов разбиения отрезка интегрирования [а, b].

Рассчитать значение интеграла с двойным шагом для определения апостериорной погрешности.

3. Найти необходимое количество интервалов разбиения n, произвольно задав интеграл, содержащий трансцендентную функцию, для вычисления интеграла с точностью 10 ^-4.

4. Вычислить с помощью математических пакетов MATHCAD, MATLAB приближенное значение определенного интеграла функции f(x) на интервале [a, b] для произвольного числа интервалов разбиения n, а также приближенное значение интеграла, использовав методы левых, правых, средних прямоугольников, трапеций и Симпсона. Оформить все вычисления в одном программном блоке.

5. Оценить посредством математических пакетов MATHCAD, MATLAB априорную погрешность вычисления приближенного интеграла для каждой из квадратурных формул. Оформить все вычисления в одном программном блоке.

6. Оценить посредством математических пакетов MATHCAD, MATLAB апостериорную погрешность вычисления приближенного интеграла для каждой из квадратурных формул. Оформить все вычисления в одном программном блоке.

7. Выполнить расчет заданного варианта. Построить график функции f(x).

8. Проверить полученные результаты с помощью встроенных функций пакетов.

Содержание отчета

1. Постановка задачи.

2. Теоретические сведения.

3. Ручной счет с использованием всех квадратурних формул.

4. Листинги счета на ЭВМ.

Теоретические сведения

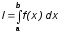
Численное интегрирование необходимо тогда, когда через элементарные функции нельзя аналитически записать первообразную интеграла или если запись первообразной имеет сложный вид.

Суть большинства методов вычисления определенных интегралов заключается в замене подынтегральной функции f(х) аппроксимирующей g(х), для которой можно легко записать первообразную в элементарных функциях, т. е.

, (3.1)

где I – приближенное значение интеграла; R – погрешность вычисления интеграла.

Методы численного интегрирования можно сгруппировать в зависимости от способа аппроксимации подынтегральной функции.

Приведем краткую характеристику групп наиболее распространенных методов:

• Методы Ньютона − Котеса ― основаны на полиноми-альной аппроксимации подынтегральной функции. Алгоритмы методов просты и легко поддаются программной реализации.

• Сплайновые методы ― базируются на аппроксимации подынтегральной функции сплайнами, представляющими собой кусочный полином. Они различаются по типу выбранных сплайнов.

• Методы наивысшей алгебраической точности ― используют неравноотстоящие узлы, обеспечивающие минимальную погрешность интегрирования для наиболее сложных функций при заданном количестве узлов.

• Методы Монте – Карло ― узлы выбирают с помощью датчика случайных чисел, результат вычисления интеграла носит вероятностный характер, эффективны при вычислении интегралов большой кратности.

• Специальные методы, алгоритмы которых разрабатываются с учетом особенностей конкретных подынтегральных функций.

Независимо от выбранного метода в процессе численного интегрирования необходимо вычислить приближенное значение интеграла (3.1) и оценить погрешность R. Последняя будет уменьшаться при увеличении количества разбиений n интервала интегрирования [а, b] в результате более точной аппроксимации подынтегральной функции. Однако при этом возрастает погрешность суммирования частичных интегралов. Заметим, что последняя погрешность начиная с некоторого значения n₀ будет преобладающей. Это должно предостеречь от выбора чрезмерно большого числа n и привести к необходимости разработки способа оценки погрешности R для выбранного метода интегрирования.

Рассмотрим простейшие методы из класса методов Ньютона – Котеса.

Один из методов приближенного интегрирования – метод прямоугольников. Суть метода заключается в следующем. Участок интегрирования [a, b] разделяют на n равных частей и получают точки x₀ = a, x₁, x₂,…,x_n-1, x_n = b. Расстояние между соседними точками (шаг) равно . Подынтегральную функцию f(x) на элементарном интервале интегрирования заменяют полиномом нулевой степени. Подобная замена неоднозначна, так как константу можно выбрать равной значению подынтегральной функции в любой точке в интервале интегрирования. Приближенное значение интеграла на элементарном участке определяют как площадь прямоугольника, одна из сторон которого – длина отрезка интегрирования, а другая – аппроксимирующая константа.

Площадь криволинейной трапеции, т.е. искомый интеграл, приближенно заменяют суммой площадей прямоугольников, образуемых отрезками разбиения и значениями подынтегральной функции в левых или правых концах этих отрезков.

Формула метода левых прямоугольников

.

Формула метода правых прямоугольников

.

Геометрическая интерпретация приведенных формул показана на рис. 3.1 , 3.2.

Рис. 3.1. Метод левых прямоугольников

Рис. 3.2. Метод правых прямоугольников

Остаточный член для формул прямоугольников определяется как

где .

Очевидно, чем больше число n отрезков разбиения, тем более точный результат будут иметь приведенные формулы. Однако увеличение отрезков разбиения промежутка интегрирования ведет, как было отмечено, к увеличению погрешности вследствие погрешности округления. Поэтому большой интерес представляют методы, которые дают более точные результаты при том же количестве разбиений n. Самые простые – это методы средних прямоугольников и трапеций.

Если в качестве значений функции использовать средние точки отрезков разбиения, то получим формулу метода средних прямоугольников

.

Остаточный член для формул средних прямоугольников определяется соотношением

где .

Если на каждом частичном отрезке , подынтегральную функцию заменить интерполяционным многочленом первой степени, построенным по двум узлам интерполяции ( и ), т.е. дугу графика подынтегральной функции заменить стягивающей её хордой, то получаем приближённое равенство – квадратурную формулу трапеций

.

Суммируя значения интегралов по всем отрезкам, находим общую квадратурную формулу трапеций

.

Погрешность этой формулы (остаточный член)

где .

Квадратурная формула Симпсона. Приближённое значение определённого интеграла можно вычислить и другим способом. Разбиваем отрезок на равных частей (– чётное). Рассмотрим отрезки , , …, .

На каждом сдвоенном отрезке функцию заменяем интерполяционным многочленом второй степени, построенным по трём узлам интерполяции (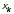, , ), т.е. дугу графика подынтегральной функции на каждом сдвоенном отрезке заменяем параболой, проходящей через точки , , 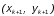. Получаем приближённое равенство

.

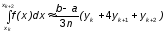Сумма интегралов по всем сдвоенным частичным отрезкам дает общую формулу Симпсона

Погрешность этой формулы

где .

Апостериорная оценка погрешности квадратурных формул

Обозначим через , приближённые значения определённого интеграла, вычисленные по одной из квадратурных формул с шагом и .

Отметим, что найти несложно, так как не требуется вычислять новые значения подынтегральной функции. Погрешность квадратурной формулы при вычислении интеграла с шагом удовлетворяет неравенствам:

– для формул левых и правых прямоугольников

– для формул трапеций и средних прямоугольников

;

– для формулы Симпсона

.

Все приведенные квадратурные формулы, формулы для вычисления остаточного члена (априорной погрешности) и оценки апостериорной погрешности (формулы Рунге) сведены в табл. 3.1.

Таблица 3.1

№ п/п	Название метода	Расчетная формула	Порядок метода	Априорная погрешность вычислений	Апостериорная погрешность вычислений
1	Левых пря-моуголь- ников		1h

Окончание табл.3.1

№ п/п	Название метода	Расчетная формула	Порядок метода	Априорная погрешность вычислений	Апостериорная погрешность вычислений
2	Правых прямо-угольников		1h
3	Средних прямо-угольников		hh2
4	Трапеций		hh2
5	Симпсона		hh4