2*. Дисперсія дискретної випадкової величини, властивості

Математичне сподівання випадкової величини є середнім очікуваним значенням цієї величини, або є точкою на числовій осі, біля якої розкидані можливі значення випадкової величини. Але цього не досить для повної характеристики випадкової величини бо можливі значення випадкової величини більш або менш бувають розкидані біля математичного сподівання. Це явище називається розсіюванням випадкової величини. Так наприклад, дві випадкові величини і мають однакові математичні сподівання. З цього прикладу ми бачимо, що можливі значення випадкової величини більше розкидані (розсіяні)

біля математичного сподівання ніж у випадкової величини . Для кількісної оцінки розсіювання можливих значень випадкової величини біля її математичного сподівання користуються числовими характеристиками випадкової величини, які називаються дисперсією і середнім квадратичним відхиленням. Ці величини і є мірою розсіювання можливих значень випадкової величини біля її математичного сподівання.

Дисперсія дорівнює математичному сподіванню квадрата відхилення випадкової величини від її математичного сподівання, яка позначається так:

,

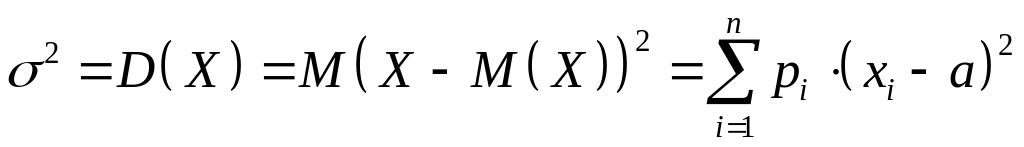де .

Для практичного обчислення дисперсії зручно користуватися другою формулою, яка отримується з попередньої формули:

.

Властивості дисперсії

Властивість 1. Дисперсія сталої величини дорівнює нулю

.

Доведення. За означенням дисперсії

Використовуючи властивість математичного сподівання (математичне сподівання сталої дорівнює самій сталій), отримаємо:

.

Отже, .

Властивість стане ясною, якщо врахувати, що стала величина зберігає одне й те ж значення і розсіяння немає.

Властивість 2. Сталий множник можна виносити за знак дисперсії, підводячи його до квадрату

.

Доведення. За означенням дисперсії

.

Користуючись властивістю математичного сподівання (сталий множник можна виносити за знак математичного сподівання), отримаємо

.

Властивість стане ясною, якщо прийняти до уваги, що при величина має можливі значення (по абсолютній величині), більші ніж величина . Звідси маємо, що ці значення розсіяні біля математичного сподівання більше, ніж можливі значення біля , тобто . Навпаки, якщо , то .

Властивість 3. Дисперсія суми двох незалежних випадкових величин дорівнює сумі їх дисперсій

.

Доведення. За формулою для обчислення дисперсії маємо

.

Розкривши дужки і користуючись властивостями математичного сподівання суми декількох величин і добутку двох незалежних випадкових величин, отримаємо

.

Отже, .

Наслідок 1. Дисперсія суми декількох взаємно незалежних випадкових величин дорівнює сумі дисперсій цих величин

.

Наслідок 2. Дисперсія суми сталої величини і випадкової дорівнює дисперсії випадкової величини:

.

Властивість 4. Дисперсія різниці двох незалежних випадкових величин дорівнює сумі їх дисперсій:

.

Доведення. За третьою властивістю

За другою властивістю

або .

Властивість 5. Дисперсія числа появи події в незалежних дослідах, в кожнім з яких ймовірність появи події стала, дорівнює добутку числа дослідів на ймовірність появи і не появи події в одному іспиті:

.

(Доведення провести самостійно).

Для практичного користування дуже важливим є твердження: математичне сподівання середнього арифметичного

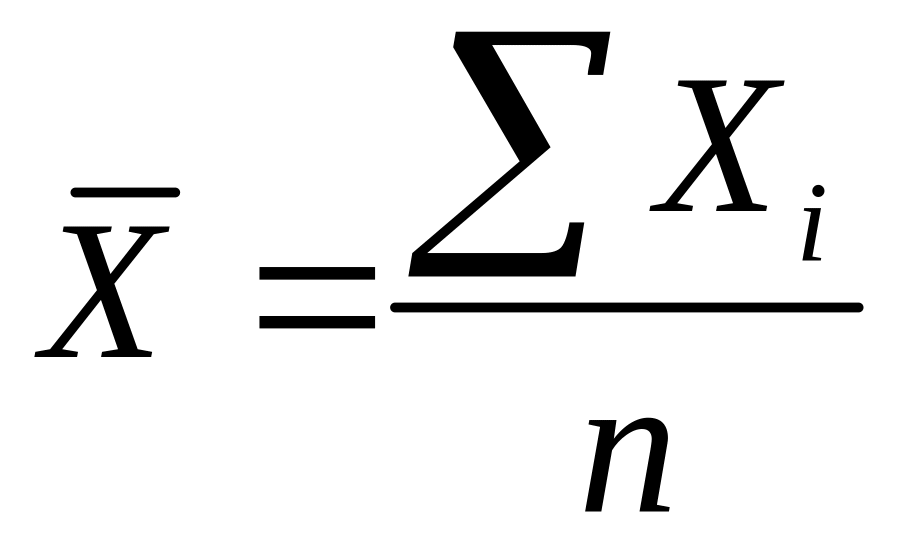
Однаково розподілених незалежних випадкових величин , ,…, дорівнює математичному сподіванню кожної з них, а дисперсія випадкової величини в разів менша дисперсії кожної з них, тобто

,

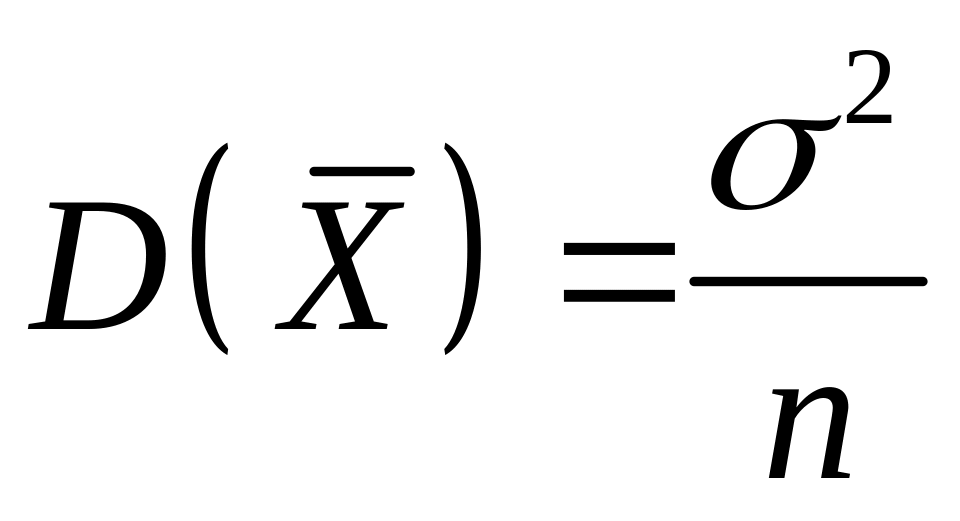де , .

, де , .

Таким чином, наприклад, середнє арифметичне ряду вимірів дає більш достовірний (вірогідний) результат, ніж окремий вимір. Із зростанням числа вимірів достовірність (вірогідність) середнього арифметичного числа вимірів зростає.