28 Двойной интеграл как оббьем под графиком функции. Двойной интеграл как масса пластины.

Если z = f (x;y) непрерывна в области D R² и f (x;y) ≥ 0, то двойной интеграл от этой функции по области D равен объему цилиндроида, у которого нижнее основание – область , верхнее – часть поверхности z = f (x;y) и боковая поверхность цилиндроида параллельна 0Z, т.е.

2. Масса пластинки, занимающей область D плоскости 0XY и имеющей плотность :

При этом статистические моменты пластинки, относительно осей 0X и 0Y:

; .

29.Основные свойства двойного интеграла.

1.

2.

3.

4. , если f(x,y)>=α(x,y)

5.

6. Если ф-ия f(x,y) непрерывна в замкнутой области D, площадь кривой S, то m. m и M-наибольшее и наименьшее значение подинтегральной функции в области D.

7.F(x0 , y0)=- средним значением функции f(x,y) в области D.

32.Формула Грина.

Теорема Грина. Если плоское векторное поле F(x,y)=[fX(x,y);fY(x,y)]t непрерывно дифференцируемо в замкнутой области DК ÌR2, ограниченной гладким контуром «К», криволинейный интеграл по замкнутому контуру в положительном направлении (+К) равен двойному интегралу по области, ограниченной этим контуром

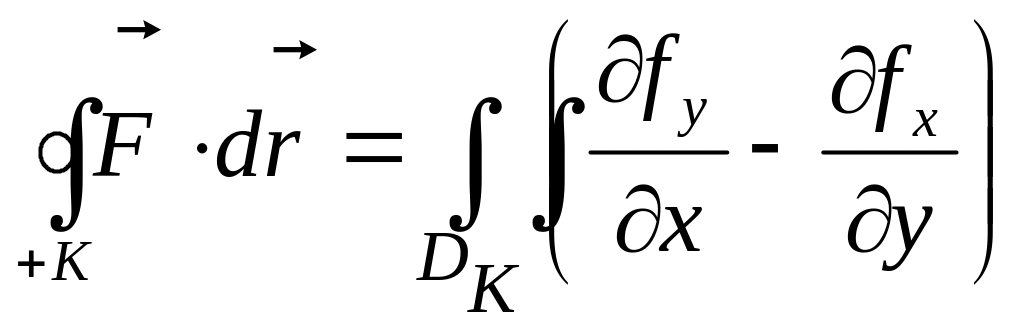- формула Грина

30.Криволинейные интегралы первого рода и его свойства. Формулы для вычисления криволинейного интеграла первого рода. Определение Пусть кривая C описывается векторной функцией где переменная s представляет собой длину дуги кривой (рис. 1)

если на кривой C определена скалярная функция F, то интеграл называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как Криволинейный интеграл существует, если функция F непрерывна на кривой C

Свойства криволинейного интеграла первого рода

Криволинейный интеграл I рода обладает следующими свойствами:

Интеграл не зависит от ориентации кривой;

Если гладкая кривая C задана параметрически соотношением и скалярная функция F непрерывна на кривой C, то

Если C является гладкой кривой в плоскости Oxy, заданной уравнением

Если гладкая кривая C в плоскости Oxy определена уравнением

В полярных координатах интеграл выражается формулой

где кривая C задана в полярных координатах функцией

31. Криволинейный интеграл 2 рода.

Пусть функции P(x, y) и Q(x, y) непрерывны в точках дуги АВ гладкой кривой К, имеющей уравнение

О п р е д е л е н и е. Интегральной суммой для функций P(x, y) и Q(x, y) по координатам называется сумма вида

где - проекции элементарной дуги на оси Ох и Оу.

оп р е д е л е н и е. Криволинейным интегралом по координатам (или криволинейным интегралом второго рода) от выражения P(x, y)dx + Q(x, y)dy по направленной дуге АВ называется конечный предел интегральной суммы (131) при стремлении и к нулю.

Свойства:

Криволинейный интеграл 2-го рода меняет свой знак на противоположный при изменении направления пути интегрирования.

33.Поверхностный интеграл первого рода.

Предел поверхностной интегральной суммы первого рода при безграничном ростре числа областей дробления σ1, σ2, … , σ n и стремления к нулю длины контуров всех областей дробления называется поверхностным интегралом первого рода

Формулы:

1Линейное свойство

2

3 Аддитивное свойство по области интегрирования

4

34.Тройной интеграл. Сведение тройного интеграла к двойному интегралу.

Определение. Тройным интегралом от функции f(x, y, z) по области Ω называется предел интегральной суммы , если он существует.

Тройной интеграл обозначается

Пусть V- ограниченная замкнутая пространственная область, границей которой является кусочно-гладкая поверхность, и пусть функция  определена и ограничена в V. Посредством сетки кусочно-гладких поверхностей разобьем Vна конечное число элементарных областей   с объемами (разбиение Z). Пусть . наибольший из диаметров областей  , получающийся при разбиении Z. В каждой из элементарных областей выберем произвольную точку . Число ставится в соответствие каждому разбиению  Z и каждому выбору точек и называется интегральной суммой. Если существует   и он не зависит от выбора разбиения Z и точек, то функция называется интегрируемой по Риману в области V , а сам предел называется тройным интегралом от функции   по области  V и обозначается  . Свойства тройных интегралов такие же, как и у двойных интегралов.