30Свойства бесконечно малых и бесконечно больших функций

1. Число А является пределом функции f(x) в точке х₀ тогда и только тогда, когда существует бесконечно малая функция при такая, что .

2. Сумма и произведение конечного числа бесконечно малых (бесконечно больших) функций при является бесконечно малой (бесконечно большой функцией).

3. Произведение бесконечно малой при функции на ограниченную функцию является бесконечно малой.

4. Частное при делении постоянной С, на бесконечно малую при является бесконечно большой при

5. Частное при делении постоянной С на бесконечно большую при является бесконечно малой при

При вычислении пределов функций удобно применять метод замены переменной, т.е. , где , если .

Замечательные пределы

При вычислении пределов в случае неопределенностей часто используют специальные формулы, которые называются замечательными пределами.

В 31.Первый замечательный предел

(7)

Как следствие формулы (7) справедливы формулы

Второй замечательный предел

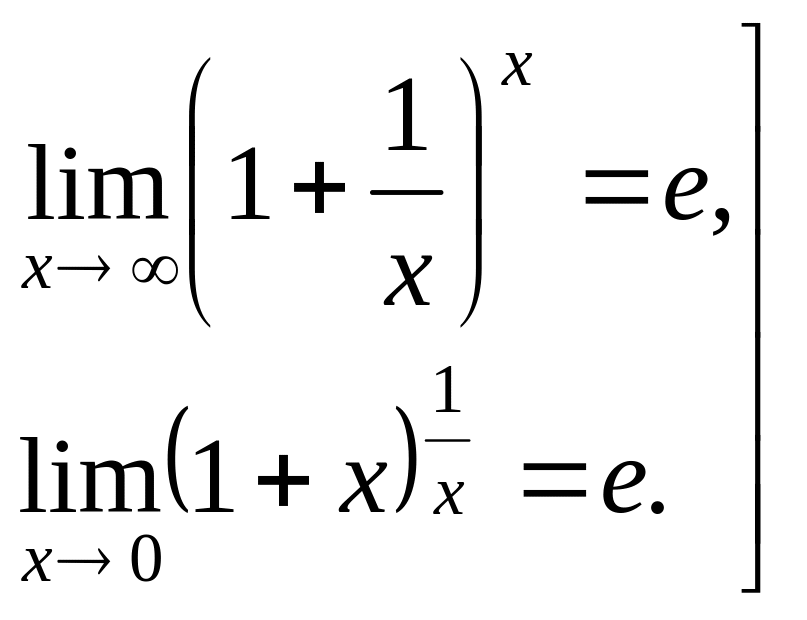(8)

Третий замечательный предел

(9)

в частности,

Четвертый замечательный предел

(10)

в частности,

Пятый замечательный предел

(11)

Указанные формулы (7)–(11) замечательных пределов обобщаются на любую функцию u(x), стоящую вместо независимой переменной х при условии, что если (или ) во всех формулах кроме (8), в которых

Обобщенная таблица замечательных пределов

;

; ; (12)

; ; (13)

; ; (14)

. (15)

При использовании обобщенных форму на практике вместо (под знаком предела пишут указанное в условии: .

Все приведенные формулы обобщенной таблицы замечательных пределов (кроме формул (12)) раскрывают неопределенность типа . Формулы (12) раскрывают неопределенность типа .

Эквивалентность функции

Две функции и называются эквивалентными бесконечно малыми, при , если

,

это записывают при .

При вычислении пределов функций в точке и на бесконечности удобно пользоваться следующей теоремой:

Если , и - некоторые функции, определенные в

окрестности точки (на числовой полуоси) и при

, то

. (16)

Формула (16) показывает, что в произведении можно заменять функцию – сомножитель на эквивалентную ей – более простую для вычисления предела.

Таблица эквивалентных бесконечно малых

Пусть , если . Тогда справедливы следующие эквивалентности:

; (17)

; (18)

; (19)

; (20)

; (21)

(22)

(23)

(24)

В.49.Односторонние пределы: Асимптоты графика функции.

Левой (правой) полуокрестностью точки называется произвольный интервал , где слева (справа).

Число А называется пределом функции в точке слева (справа), если функция определена в некоторой левой (правой) полуокрестности точки и если для любого существует такое, что для всех , удовлетворяющих условию , выполняется неравенство

.

В этом случае пишут

Пределы слева и справа называются односторонними пределами. Если , то односторонние пределы обозначают , .

Функция имеет предел в точке тогда и только тогда, когда в этой точке существуют оба односторонние предела, равные между собой.

В этом случае их общее значение и является пределом функции в точке

.

Асимптота графика функции - это прямая линия, к которой неограниченно приближается график данной функции, когда его точка неограниченно удаляется от начала координат.

Различают горизонтальную, вертикальную и наклонную асимптоты.

Прямая называется вертикальной асимптотой, графика функции , если

или .

В случае вертикальной асимптоты функция является бесконечно большой в точке .

Прямая называется горизонтальной асимптотой графика функции , если .

Вертикальные асимптоты могут существовать у функций, которые определены не на всей числовой прямой.

Если областью определения функции является вся числовая прямая, то у функции нет вертикальных асимптот.

Прямая называется наклонной асимптотой графика функции , при , если

.

Для нахождения коэффициентов и b применяют следующие формулы:

(25)

(26)

Если хотя бы один из этих пределов равен или не существует, то у функции наклонных асимптот нет.

Если , , то прямая является горизонтальной асимптотой. Горизонтальная асимптота – это частный случай наклонной асимптоты.

Заметим, что наклонных асимптоты у функции может быть не больше двух, а вертикальных может быть сколько угодно.

В33.. Непрерывность функции. Классификация

точек разрыва.

Функция называется непрерывной в точке , если она определена в этой точке в некоторой ее окрестности и

(27)

Если функция непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.

Существуют и другие определения непрерывности функции в точке. Функция называется непрерывной в точке , если она определена в этой точке и в некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:

(28)

Непрерывность функции в точке определяется также на основе односторонних предметов.

Функция называется непрерывной в точке , если она определена в этой точке и некоторой ее окрестности и существует односторонние пределы (конечные) такие, что

(29)

Свойства непрерывных функций

1. Если функции и непрерывны в точке , то их сумма также есть непрерывная функция в точке . Это свойство справедливо для любого конечного числа слагаемых.

2. Произведение двух непрерывных функций есть функция непрерывная.

3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

4. Если функция непрерывна в точке и , то значения функции в некоторой окрестности точки имеют тот же знак, что и .

5. Если функция непрерывна в точке и принимает в этой точке значение , а функция непрерывна в точке , то сложная функция непрерывна в точке .

6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

7. Если непрерывная на некотором обрезке функция принимает на его концах значение разных знаков, то на этом отрезке найдется хотя бы одна точка, в которой .

8. Если функция непрерывна в точке , то операция вычисления предела в этой точке и функции переставимы, т.е.

(30) На свойстве 8 (равенства (30)) и было основано непосредственное вычисление предела функции в случае отсутствия неопределенности (см.параграфы 16.1 – 16.4).

Если нарушается хотя бы одно условие, указанное в определении непрерывности, то называется такой разрыв функции.

Классификацию точек разрыва дают в зависимости от того, какое условие последнего определения непрерывности (в том числе равенства (29)) нарушено.

Точки разрыва I рода

1. Если существуют односторонние пределы в точке (конечные) и

,

то называется точкой устранимого разрыва.

2. Если существует односторонние пределы в точке (конечные) и , (44)

то - точка разрыва, который называется скачок.

В случае устранимого разрыва функцию можно доопределить в точке значением и она станет непрерывной.

В случае скачка сделать это невозможно.

Точки разрыва II рода

1. Если

или

то – точка разрыва, который называется бесконечный скачок. В этом случае прямая является вертикальной асимптотой.

2. Если односторонние пределы в точке не существуют (не определены), то - точка неопределенности.

Получили, что – точка разрыва I рода (скачка). Значит, функция непрерывна всюду на числовой прямой кроме точки , в которой она имеет скачок, равный 1.

В41.Дифференцирование функции с переменной в основании степени и в показателе

Производная функции

, (1)

где – некоторые выражения с переменной x, не может быть вычислена по табличным формулам дифференцирования степенной функции и показательной функции (так как переменная находится как в основании степени, так и в её показателе). Заданная функция типа (1) называется показательно-степенной.

Способы вычисления производной показательно-степенной функции

Первый способ вычисления

Используют метод логарифмического дифференцирования. Для этого:

1. логарифмируют обе части уравнения, которым задается функция (например, по основанию ):

,

получают

;

2. дифференцируют обе части полученного равенства, где считают 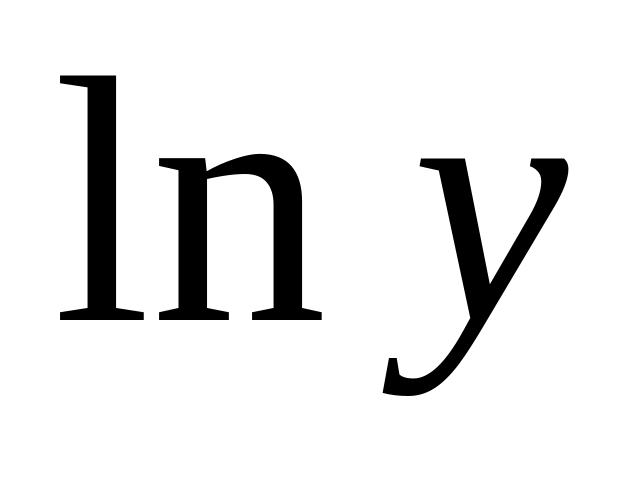сложной функцией от (правую часть равенства дифференцируют как произведение функций):

3. выражают из полученного равенства :

;

4. заменяют y его выражением через x:

. (2)

При решении данным методом используют не конечную формулу (2), а реализуют процесс логарифмического дифференцирования для каждой функции типа (1).

Второй способ

На основании свойства логарифмов записывают

. (3)

Далее дифференцируют как сложную функцию.

С помощью логарифмического дифференцирования удобно также вычислять производные функций при наличии в их аналитическом задании большого количества операций умножения, деления, возведения в степень.

Дифференцирование функций, заданных неявно и параметрически.

Уравнение

(4)

задаёт неявно функцию , если при подстановке выражения вместо в уравнение (4) оно превращается в тождество. Предположим, что функция дифференцируема и требуется вычислить

Первый способ: Если практически возможно, выражают y через x и дифференцируют y(x) по правилам дифференцирования.

Второй способ: Дифференцируем уравнение (4) по , считая, что y есть функция от x. Получаем новое уравнение, содержащее x, y и . Из него находим

Пусть функция задана параметрически уравнениями:

, (5)

где функции и дифференцируемы для любого , причем , и требуется найти

Первый способ: Из первого уравнения системы (5) выражают t через x (если это возможно) и подставляют во второе уравнение системы (5). Приходят к сложной функции от переменной , которую дифференцируют по .

Второй способ: Используют формулу

(6)

Полученное таким образом выражение для зависит от переменной . Если возможно (и необходимо) из первого уравнения системы (5) выражают через и подставляют выражение, полученное для

В46.Необходимое и достаточное условия

Дифференцируемости функций. Дифференциал функции

Функция называется дифференцируемой в точке если ее приращение в этой точке может быть представлено в виде

(7)

где . (8)

Теорема: Для того, чтобы функция была дифференцируема в точке необходимо и достаточно, чтобы в точке существовала производная и в равенстве (7) выполнялось .

Понятие дифференцируемости функции эквивалентно равенству

(9)

где – главная часть приращения функции, а для бесконечно малой выполняется (8).

Дифференциалом функции в точке называется главная часть приращения функции. Дифференциал обозначается символом . По определению

(10)

В частности, для получим .

Тогда определение дифференциала имеет вид:

Свойства дифференциала

Пусть – дифференцируемые функции на некотором множестве .

1)

2)

3)

4)

5)

6) где – сложная функция, дифференцируемая по переменной u (свойство инвариантности дифференциала). При достаточно малом значении приращение функции с большой степенью точности можно заменить дифференциалом функции:

(11)

Формулу (11) используют в приближенных вычислениях.

С геометрической точки зрения дифференциал функции равен приращению ординаты касательной к кривой в точке , когда аргумент получает приращение

В43. Производные и дифференциалы высшего порядка

Производная определенная на некотором множестве является также функцией от x. В случае ее дифференцируемости можно вычислить ее производную. Производная от производной называется производной второго порядка:

Аналогично .

Начиная с четвертого, порядок производной обозначается только индексом в скобках (сверху). Производные порядка 1–3 также обозначаются По определению В случае дифференцируемости производной производная порядка n определяется равенством

(12)

Для производных высшего порядка справедливо свойство линейности:

где – произвольные действительные числа,

– n раз дифференцируемые функции.

Если и – n раз дифференцируемые функции, то верна формула Лейбница:

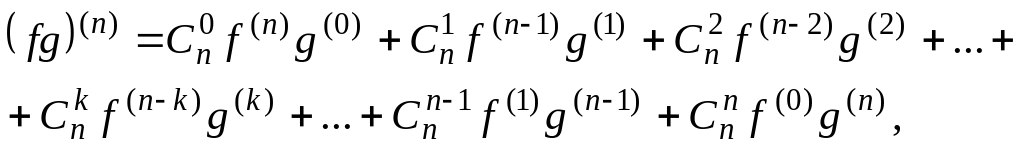(13)

где – биномиальные коэффициенты:

.

Коэффициенты можно найти также из треугольника Паскаля. Если функция задана в неявном виде уравнением то для нахождения производной второго порядка (в случае ее существования) надо продифференцировать найденную первую производную по аргументу x, продолжая рассматривать y как функцию от x. Затем вместо надо подставить найденное ранее значение.

Если функция задана параметрически,

То находим вначале производную 1-го порядка по формуле (6) и затем

(14)

Для нахождения производной второго порядка используем формулу (6) к параметрически заданной функции (14):

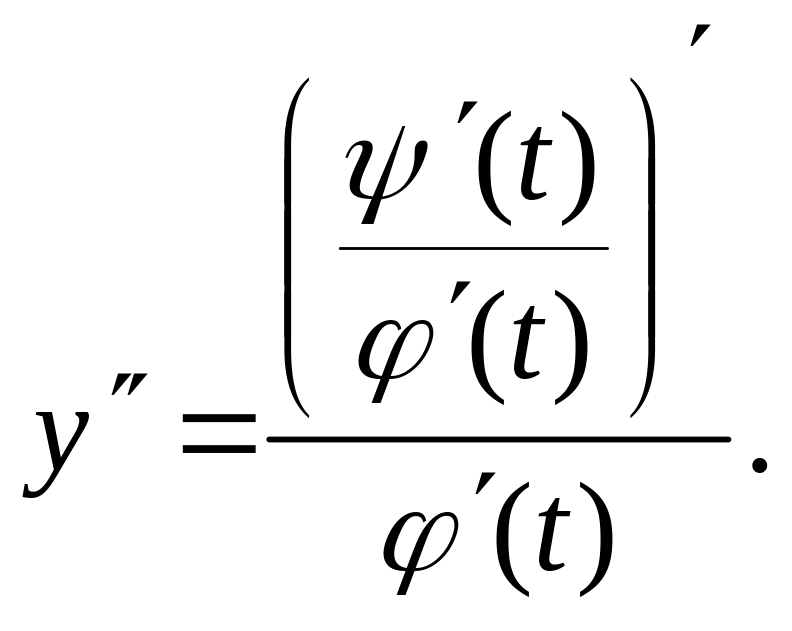
Аналогично реализуем тот же подход при нахождении и т. д.

Дифференциал от дифференциала функции f в точке x (если функция определена и дважды дифференцируема) называется дифференциалом второго порядка:

Дифференциал n-го порядка функции (в случае дифференцируемости n раз, ) определяется как дифференциал от дифференциала (n–1)-го порядка:

Для вычисления дифференциала порядка n используют формулу:

(15)

Дифференциалы второго и выше порядков не обладают (в отличие от дифференциалов первого порядка) свойством инвариантности, т. е. их форма, а следовательно и способ вычисления зависят от того, является ли аргумент x независимой переменной или дифференцируемой функцией другой переменной.

В44,45. Правило Лопиталя. Формула Тейлора

В случае неопределенностей и при вычислении пределов часто бывает полезным применять правило Лопиталя, которое задается следующей Теоремой.

Теорема 1. Пусть функции и удовлетворяют следующим условиям:

1) определены и дифференцируемы на интервале (a; b), за исключением быть может точки причем и

2) (либо );

3) существует предел тогда существует предел отношений функций причем

(17)

Правило Лопиталя можно использовать последовательно несколько раз.

Аналогичное правило верно в случае

Если при вычислении пределов возникает неопределенность иного вида, то в начале их необходимо свести к неопределенности вида , , а затем использовать правило Лопиталя.

В частности, выражения, которые приводят к неопределенностям тождественно преобразуют к такому выражению, которое приводят к неопределенности или . Неопределенность вда возникают при рассмотрении функции типа С помощью тождества

(18)

они сводятся к неопределенности

Если функция имеет в некоторой окрестности точки производные до -го порядка включительно, то при верна формула Тейлора

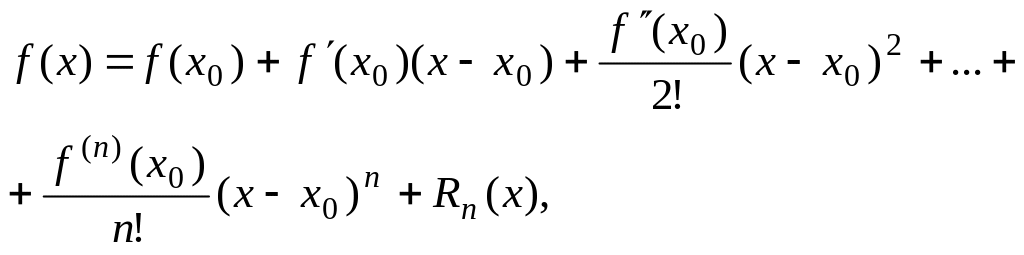(19)

где – остаточный член формулы Тейлора.

Существует несколько форм записи остаточного члена. В частности, в форме Логранжа:

.

Если в формуле Тейлора получим частный вид формулы Тейлора, называемый формулой Маклорена:

где

Верны следующие формулы Маклорена:

(20)

где

где

(21)

где

(22)

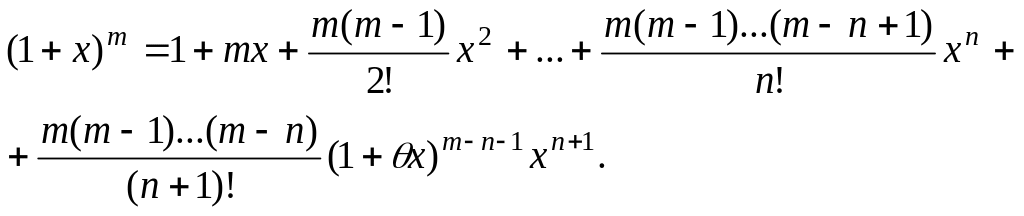
Формулы Маклорена могут быть использованы в приближенных вычислениях. При этом абсолютная погрешность приближения в случае чередования знаков в формуле Маклорена не превосходит абсолютной величины первого отображаемого слагаемого.

Исследование функций. Наибольшее

и наименьшее значение функций на промежутке

Всюду далее функция определена на рассматриваемых промежутках.

Теорема 1. Дифференцируемая на функция (убывает) на этом интервале тогда и только тогда, когда

Точка называется точкой локального максимума (минимума) функции , если существует некоторая окрестность точки такая, что для всех x из этой окрестности выполняется неравенство .

Значение называется локальным максимумом (минимумом) функции.

Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются экстремумом функции.

Теорема 2 (необходимое условие существования экстремума функции).

Если в точке функция достигает экстремума, то ее производная в этой точке равна нулю или не существует. Точки, в которых производная функции обращается в нуль или не существует, называют критическими. Исследование функции на экстремум начинается с нахождения критических точек. Однако не в каждой критической точке существует экстремум. Для того, чтобы определить точки экстремума используют достаточные условия (признаки экстремума).

Теорема 3 (первый признак экстремума функции).

Пусть – критическая точка непрерывной функции .

Если в некоторой окрестности точки выполняется условие

то – точка локального максимума;

если выполняется условие

то – точка локального минимума.

Если производная имеет один и тот же знак в левой и правой полуокрестности точки , то не является точкой экстремума.

Теорема 4 (второй признак экстремума функции).

Пусть – критическая точка функции , дважды дифференцируемой в окрестности точки . Тогда является точкой локального минимума функции , если и точкой локального максимума, если

Теорема 5 (третий признак экстремума функции).

Пусть – n раз непрерывно дифференцируемая в критической точке функция и Тогда:

1) если n – четное и то – точка локального максимума;

2) если n – четное и то – точка локального минимума;

3) если n – не четное, то не является точкой локального экстремума.

Точка называется точкой глобального максимума (минимума) функции на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство .

Точки глобального максимума и минимума называются точками глобального экстремума. Значения функции в этих точках называются соответственно глобальным максимумом (наибольшим значением) и глобальным минимумом (наименьшим значением).

Теорема 5 (Вейерштрасса). Если функция непрерывна на отрезке , то она достигает на нем своих наименьшего и наибольшего значений

Непрерывная на отрезке достигает наименьшего (наибольшего) значений либо на концах отрезка, либо в точках ее локального экстремума.

Для отыскания глобальных экстремумов функции на отрезке необходимо:

1) найти производную

2) найти критические точки функции;

3) найти значения функции на концах отрезка, т. е. и а также в критических точках, принадлежащих

4) из всех полученных значений функции определить наибольшее и наименьшее ее значения.

График функции называется вогнутым (выпуклым вниз) на , если дуга кривой на этом интервале расположена выше любой касательной проведенной к графику этой функции (рис. 1).

Рис. 1.

График функции называется выпуклым (выпуклым вверх) на , если дуга кривой на этом интервале расположена ниже любой касательной проведенной к графику этой функции (рис. 2).

Рис. 2.

Теорема 6. Если функция дважды дифференцируема на и всюду на этом интервале, то график функции вогнут (выпуклый) на .

Точка така, что график функции меняет выпуклость на вогнутость или наоборот, проходя через , называется точкой перегиба (рис. 3)

Рис. 3.

Для нахождения точек перегиба вначале находят критические точки 2-го рода – те значения x, для которых или не существует. Далее используют достаточные условия перегиба.

Теорема 7 (достаточные условия перегиба).

Если для функции вторая производная в некоторой точке обращается в нуль или не существует и при переходе через нее меняет свой знак, то – точка перегиба.

План исследования функции и построения графика

1. Найти область определения функции .

2. Найти область значений (если это возможно вначале, часто можно указать только по результатам исследования).

3. Исследовать функцию на четность.

4. исследовать на периодичность.

5. Найти точки пересечения с осями Ox (нули функции) и Oy.

6. Найти промежутки знакопостоянства функции.

7. Исследовать на непрерывность, дать классификацию разрывов.

8. Найти асимптоты графика функции (горизонтальную, вертикальную, наклонную).

9. Исследовать на монотонность и экстремум.

10. Исследовать на выпуклость, вогнутость, перегиб.

11. Построить график функции.

12