23.Прямая и плоскость в пространстве
Пусть прямая L задана каноническими уравнениями:
![]()
где
![]()
![]() а плоскость P
– общим:
а плоскость P
– общим:
![]()
где
![]()
Тогда взаимное расположение прямой L и плоскости P в пространстве можно определить по направляющему вектору прямой L и нормальному вектору плоскости P.
1.
![]()
2.
![]()
![]()
3.
![]()
4.
![]() координаты точки пересечения могут
быть найдены следующим образом. От
канонических уравнений прямой следует
перейти к параметрическим, после чего
подставить найденные значения
координаты точки пересечения могут
быть найдены следующим образом. От
канонических уравнений прямой следует
перейти к параметрическим, после чего
подставить найденные значения
![]() в уравнение плоскости. Разрешить
полученное уравнение относительно
параметра t.
Найденное значение
в уравнение плоскости. Разрешить
полученное уравнение относительно
параметра t.
Найденное значение
![]() подставить в параметрические уравнения,
что позволит найти значения
подставить в параметрические уравнения,
что позволит найти значения
![]() которые и будут координатами искомой
точки
пересечения прямой L
и плоскости P.
которые и будут координатами искомой
точки
пересечения прямой L
и плоскости P.
Углом между и плоскостью называется угол между прямой и ее ортогональной проекцией на плоскость, т. е.
![]()
.
25. Поверхности второго порядка
Алгебраической поверхностью второго порядка называется поверхность S, общее уравнение которой в декартовой прямоугольной системе координат относительно текущих координат имеет вид
![]() где
коэффициенты при одночленах второй
степени одновременно не равны нулю.
где
коэффициенты при одночленах второй
степени одновременно не равны нулю.
Эти уравнения определяют тип поверхности и называются каноническими.
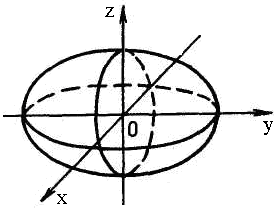
1. Эллипсоид:
![]()
2. Гиперболоид
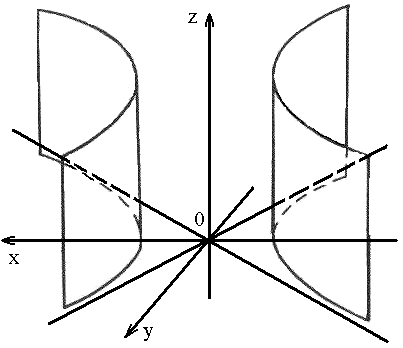
1) эллиптический:
|
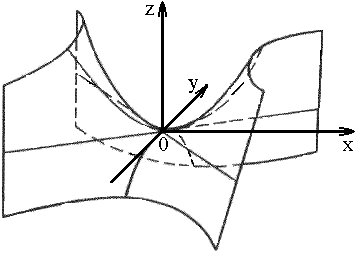
2) гиперболический:
|
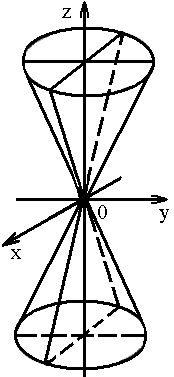
3. Конус второго
порядка:
![]()
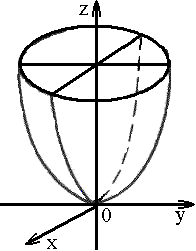
4. Параболоид
5. Цилиндр
1) эллиптический:
|
2) гиперболический:
|
3) параболический:
![]()
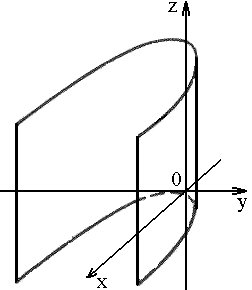
Основным методом исследования формы поверхности является метод сечений, который состоит в следующем. Поверхность пересекается координатными плоскостями и им параллельными, а затем на основании вида полученных в сечениях линий делается вывод о виде поверхности. Таким образом изучаются основные геометрические свойства невырожденных поверхностей второго порядка на основе их канонических уравнений.
При этом, когда в
общем уравнении поверхности коэффициенты
![]() приведение к каноническому виду
осуществляется с помощью метода выделения
полных квадратов и параллельного
переноса системы координат. При наличии
же в общем уравнении поверхности
смешанных произведений переменных
приведение к каноническому виду опирается
на теорию квадратичных форм.
приведение к каноническому виду
осуществляется с помощью метода выделения
полных квадратов и параллельного
переноса системы координат. При наличии
же в общем уравнении поверхности
смешанных произведений переменных
приведение к каноническому виду опирается
на теорию квадратичных форм.
В любом случае, общее уравнение поверхности может быть приведено к уравнениям, задающим так называемые вырожденные поверхности. Приведем примеры таких случаев.
1.
![]() – пустое множество точек (мнимый
эллипсоид);
– пустое множество точек (мнимый
эллипсоид);
2.
![]() – точка (0, 0, 0);
– точка (0, 0, 0);
3.
![]() – пустое множество точек
– пустое множество точек
29Предел функции в точке и на бесконечности
Определение по Коши
Число А
называется пределом
функции f(x)
в точке х0,
если функция определена в некоторой
выколотой окрестности точки х0
и если для любого сколь угодно малого
числа
![]() существует такое число
существует такое число
![]() что для всех х,
удовлетворяющих условию
что для всех х,
удовлетворяющих условию
![]() (1)
(1)
выполняется
![]() (2)
(2)
Это записывают:
![]()
Число А называется пределом функции на бесконечности, если для любого существует число что для всех х, удовлетворяющих условию
![]()
выполняется неравенство
Это записывают:
![]() (
(![]() ).
).
Определение предела функции в точке (на бесконечности) по Гейне и по Коши эквивалентны.
Функция f(x)
называется бесконечно
большой при
![]()
![]() если для всякого числа М > 0
существует
если для всякого числа М > 0
существует
![]() что для всех х,
удовлетворяющих условию
что для всех х,
удовлетворяющих условию
( )
выполняется неравенство
![]()
Это записывают:
![]()
![]() .
.
Если f(x) – бесконечно большая функция при то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.
Функция f(x) называется бесконечно малой при если
![]()
![]() .
.
Свойства предела функции в точке
1. Если функция f(x) имеет предел в точке х0, то существует окрестность этой точки (за исключением, быть может, самой точки х0), на которой функция ограничена.
2. Если существует
предел функции f(x)
в точке х0,
равный
![]() то существует такая окрестность точки
х0,
на которой функция имеет тот же знак,
что и А.
то существует такая окрестность точки
х0,
на которой функция имеет тот же знак,
что и А.
3. Если функции f(x) и g(x) имеют пределы в точке х0, то:
![]() где
где
![]()
![]() (3)
(3)
![]() (4
(4
 где
где
![]() (5)
(5)
Аналогичные свойства верны и для предела функции на бесконечности.
Если в результате
непосредственного использования формул
(3)–(5) возникает неопределенность типа
![]() то вначале необходимо тождественно
преобразовать выражение, стоящее под
знаком предела (то же для неопределенностей
то вначале необходимо тождественно
преобразовать выражение, стоящее под
знаком предела (то же для неопределенностей
![]()
![]()
![]() ).
).