Основные теоремы направленности.

/1/ с. 49-54

Фазовый центр антенны.

ХН антенны является комплексной функцией

Существуют антенны, для которых можно найти такую точку на активной поверхности, что ели поместить в нее центр сферы большого радиуса и записать ХН для этого начала отсчета, то окажется, что arg либо не меняется, либо изменяется скачком на при изменении направления. Такая точка называется фазовым центром антенны.

При вращении антенны вокруг фазового центра фаза сигнала в точке наблюдения либо совсем не меняется, либо претерпевает скачки на .

Пример: В линейной антенне с нулевым фазовым распределением фазовый центр совпадает с геометрическим центром А.

Если ХН можно представить в виде произведения некоторой вещественной функции на , то антенна имеет фазовый центр расположенный в точке, положение которой относительно начала координат характеризуется радиусом вектором .

Если же антенна не имеет фазового центра, то пользуются эквивалентным фазовым центром, называя им центр сферы наименее отличающий ее от фазового центра.

Теорема умножения.

Теорема умножения формулируется следующим образом:

ХН антенны, состоящая из n направленных одинаковых и одинаково ориентированных преобразователей, равно произведению ХН одного преобразователя и ХН гипотетической (воображаемой) антенны, составленной из n ненаправленных элементов, расположенных в фазовых центрах реальных преобразователей.

Основные ограничения при применении теоремы умножения:

- нельзя применять, если преобразователи ориентированы по разному;

- в случае цилиндрической или сферической антенны элементы должны быть звукопрозрачными или размещаться в акустически жестком экране.

Если антенна работает вне резонанса, то теорему умножения практически всегда можно использовать. Для антенны, работающей в области, близкой к резонансу, теорему умножения можно использовать, если взаимные сопротивления излучателей одинаковы, но в этом случае нужно учитывать некоторую весовую функцию, связанную с взаимодействием элементов в антенне.

Следствие:

ХН непрерывной антенны, полученной путем параллельного переноса некоторой кривой вдоль направляющей равна произведению ХН этой кривой и направляющей.

Например:

- для прямоугольника со сторонами .

Теорема умножения может быть применена последовательно несколько раз понимая под элементом не один, а группу преобразователей.

Для прозрачного цилиндра ХН равна произведению ХН направляющей и образующей.

Теорема смещения: ХН (антенны в бесконечном экране) в некоторой области L ( экрану) совпадает с ХН отрезка, являющегося проекцией рассматриваемой антенны на плоскость.

Пример 1. Рассмотрим применение теоремы смещения, когда антенна представляет собой квадрат в плоскости XOY (рис. 17) с равномерным амплитудным распределением.

y

O x

x

Рис. 17 Антенна в форме квадрата

В рассмотренном случае ХН антенны в форме квадрата совпадает с ХН отрезка, лежащего на диагонали квадрата и имеющего амплитудное распределение в виде треугольника.

Пример 2. ХН в виде круга радиусом R с равномерным распределением амплитуды в плоскости XOY совпадает с ХН отрезка, являющегося диаметром круга и имеющего амплитудное распределение,

Пример 3. Антенна представляет собой кольцо с равномерным распределением в плоскости XOY. В этом случае ХН кольца совпадает с ХН отрезка длиной , имеющего амплитудное нормированное распределение вида

Пример 4. Пусть имеется дискретная антенна, состоящая из 4-х элементов. ХН антенны, состоящей из 4-х элементов, лежащих в вершинах квадрата в плоскости XOY и с диагональю вдоль оси x, совпадает с ХН антенны, состоящей из трех элементов и обладающих амплитудным распределением 1,2,1.

Теорема сложения: Давление, развиваемое антенной, имеющее распределение колебательной скорости по всей поверхности f(S), равно сумме давлений, развиваемых такими же антеннами с амплитудными распределениями A(S) и B(S), при условии выполнения следующего равенства:

f(S)=A(S)+B(S)

В простейшем случае при равномерном распределении

Пример 1. предположим, что антенна представлена в виде 2-х отрезков (удобно, чтобы фазовые центры совпадали) длиной , а расстояние между отрезками d.

В соответствии с теоремой сложения ХН такой антенны равна разности отрезков ХН длиной и d с коэффициентом пропорциональности их длинам: Имея характеристику направленности отрезка d как

,

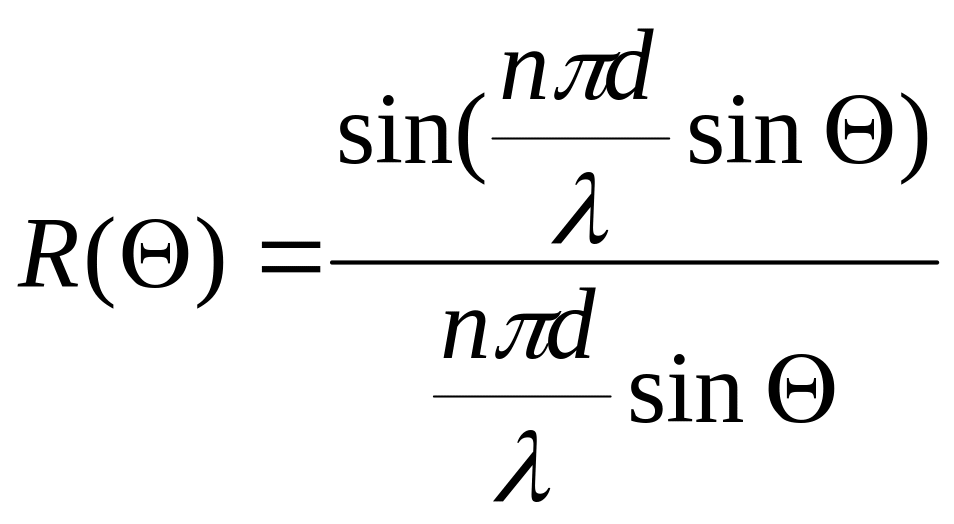в соответствии с теоремой сложения искомое выражение для ХН антенны с длиной d и запишется в виде

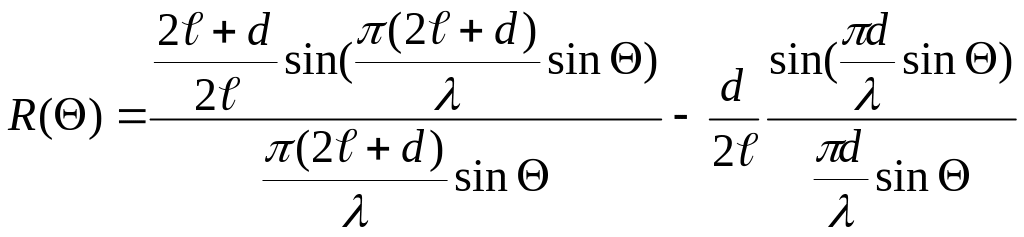
Пример 2. Пусть дана антенна в виде кольца. ХН кольца, где R – внешний радиус,

r – внутренний радиус, равна разности ХН 2-х плоских антенн в виде круга с радиусом R и r с учетом коэффициента пропорциональности их площадей:

Пример 3. Рассмотрим применение теоремы сложения для антенны, состоящей из 3-х ненаправленных элементов, расположенных на одной прямой с расстоянием между элементами d. ХН такой антенны будет равна сумме ХН антенн, составленных из 2-х крайних элементов, с расстоянием между ними 2d, и среднего элемента, с коэффициентом пропорциональности 2 и 1:

Теоремой сложения целесообразно пользоваться в тех случаях, когда антенна при распределении A(S) и B(S) имеет фазовый центр, расположенный в одной и той же точке, что позволяет производить сложения алгебраических, и не комплексных величин.