
- •1. Сутність поняття “модель”. Особливості математичної моделі.
- •3. Особливості і принципи математичного моделювання. Узагальнена схема математичного моделювання.
- •4. Поняття економіко-математичної моделі. Узагальнена схема процесу математичного моделювання економічних процесів. Особливості процесу математичного моделювання економічних систем.
- •5. Особливості економічних спостережень і вимірів.
- •6. Охарактеризуйте основні етапи економіко-математичного моделювання.
- •7. Сутність адекватності економіко-математичних моделей. Перевірка адекватності моделі.
- •8. Основні засади щодо класифікації економіко-математичних моделей. Наведіть приклади та дайте відповідні пояснення.
- •9. Сутність аналітичного та комп’ютерного моделювання.
- •10. Роль прикладних економіко-математичних досліджень.
- •11. «Павутиноподібна» модель. Гіпотези, що приймаються в моделі.
- •12. Стійка рівновага у «павутиноподібній» моделі. Умови існування стійкої рівноваги у «павутиноподібній» моделі.
- •13. Постановка задачі економіко-математичного моделювання. Сутність понять: «параметри», «змінні», «цільова функція», «система обмежень», «оптимальний план».
- •14. Предмет математичного програмування. Приклади економічних задач математичного програмування.
- •15. Багатокритеріальна оптимізація економічних систем.
- •16. Классифікація задач математичного програмування.
- •17. Загальна постановка задачі лінійного програмування. Приклади економічних задач лінійного програмування.
- •18. Форми запису задачі лінійного програмування, охарактеризувати їх. Навести відповідні формули.
- •19. Геометрична інтерпретація задач лінійного програмування. Властивості розв’язків задачі лінійного програмування.
- •Перехід від одного опорного плану до іншого
- •21. Алгоритм графічного методу розв’язування задач лінійного програмування.
- •23. 24. Умова оптимальності розв’язку задачі лінійного програмування симплекс-методом. Алгоритм симплексного методу. Навести відповідні формули.
- •25. Метод штучного базису. Ознака оптимальності плану із штучним базисом.
- •26. Двоїста задача. Правила побудови двоїстої задачі. Симетричні й несиметричні двоїсті задачі. Навести відповідні формули.
- •27. Економічний зміст двоїстої задачі й двоїстих оцінок.
- •28. Теореми двоїстості, їх економічна інтерпретація.
- •29. Застосування теорем двоїстості в розв’язуванні задач лінійного програмування. Навести відповідні формули.
- •30. Цілочислове програмування. Приклади застосування цілочислових задач в плануванні й управлінні виробництвом. Навести відповідні формули.
- •31. Геометрична інтерпретація задачі цілочислового програмування.
- •32. Загальна характеристика методів розв’язування задач цілочислового програмування.
- •33. Сутність цілочислового програмування. Графічний метод розв’язування задач цілочислового програмування.
- •34. Методи відтинання. Метод Гоморі. Навести відповідні формули.
- •35. Комбінаторні методи. Метод гілок і меж. Навести відповідні формули.
- •36. Постановка задачі нелінійного програмування, математична модель. Геометрична інтерпретація.
- •38. Основні труднощі розв’язування задач нелінійного програмування.
- •39. Графічний метод розв’язування задач нелінійного програмування.
- •40.41. Метод множників Лагранжа пошуку умовного екстремуму функції. Визначення типу екстремуму. Навести відповідні формули.
- •42. Алгоритм розв’язування задачі на безумовний екстремум. Визначення типу екстремуму. Навести відповідні формули.
- •43. Поняття про опуклі функції
- •Опуклі й угнуті функції
- •44. Сідлова точка та необхідні умови її існування. Навести відповідні формули.
- •45. Градієнтні методи розв’язання задач нелінійного програмування. Метод Франка-Вульфа розв’язування задачі нелінійного програмування. Навести відповідні формули.
- •46. Постановка зад.Динам.Прогр. Та її геометрична інтерпретація
- •47.Принцип оптимальності та алгоритм динамічного програмування.
- •50.Основні поняття та завдання теорії ігор.
- •52.Геом.Інтерпретація гри 2х2
- •54. Зведення матричної гри до задачі лінійного програмування.
29. Застосування теорем двоїстості в розв’язуванні задач лінійного програмування. Навести відповідні формули.
Між розв’язками спряжених задач крім рівності значень цільових функцій існує тісніший взаємозв’язок. Для його дослідження розглянемо дві симетричні задачі лінійного програмування.
Пряма задача:
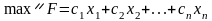
 (5.9)
(5.9)
 .
.
Двоїста задача:
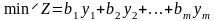
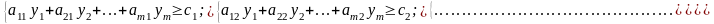 (5.10)
(5.10)
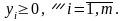
Для розв’язування задач симплексним методом необхідно звести їх до канонічної форми, для чого в системи обмежень задач (5.9) і (5.10) необхідно ввести відповідно m та n невід’ємних змінних. Поставимо обмеженням кожної задачі у відповідність змінні її двоїстої задачі.
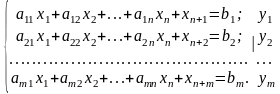
Аналогічно:
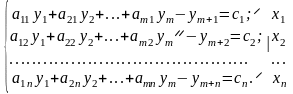
Отримали таку відповідність між змінними спряжених задач:

Економічне
тлумачення другої теореми двоїстості
щодо оптимального плану Y*
двоїстої задачі:
у разі, коли деяке j-те
обмеження виконується як нерівність,
тобто всі витрати на виробництво одиниці
j-го
виду продукції перевищують її ціну сj,
виробництво такого виду продукції є
недоцільним, і в оптимальному плані
прямої задачі обсяг такої продукції
 дорівнює нулю.
дорівнює нулю.
Якщо витрати на
виробництво j-го виду продукції
дорівнюють ціні одиниці продукції
,
то її необхідно виготовляти в обсязі,
який визначає оптимальний план прямої
задачі
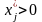 .
.
Використовуючи
третю теорему двоїстості, можна легко
визначити вплив на зміну значення
цільової функції збільшення чи зменшення
обсягів окремих ресурсів: числові
значення двоїстих оцінок показують, на
яку величину змінюється цільова функція
за зміни обсягу відповідного даній
оцінці ресурсу
 .
.
Отже, за умови незначних змін замість задачі лінійного програмування, поданій в канонічній формі
(5.14)
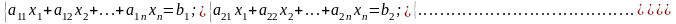 (5.15)
(5.15)
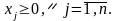 (5.16)
(5.16)
маємо
нову задачу, де
замінено на
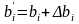 .
Позначимо через
.
Позначимо через
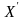 оптимальний план нової задачі. Для
визначення
оптимальний план нової задачі. Для
визначення
 не потрібно розв’язувати нову задачу
лінійного програмування, а достатньо
скористатися формулою
не потрібно розв’язувати нову задачу
лінійного програмування, а достатньо
скористатися формулою
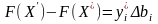 ,
де
,
де
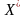 –
оптимальний план задачі (5.14-5.16).
–
оптимальний план задачі (5.14-5.16).
30. Цілочислове програмування. Приклади застосування цілочислових задач в плануванні й управлінні виробництвом. Навести відповідні формули.
Задача математичного програмування, змінні якої мають набувати цілих значень, називається задачею цілочислового програмування. У тому разі, коли цілочислових значень мають набувати не всі, а одна чи кілька змінних, задача називається частково цілочисловою.
До цілочислового програмування належать також ті задачі оптимізації, в яких змінні набувають лише двох значень: 0 або 1 (бульові, або бінарні змінні).
Умова цілочисловості є по суті нелінійною і може зустрічатися в задачах, що містять як лінійні, так і нелінійні функції. Розглянемо задачі математичного програмування, в яких крім умови цілочисловості всі обмеження та цільова функція є лінійними, що мають назву цілочислових задач лінійного програмування.
Загальна цілочислова
задача лінійного програмування
записується так: 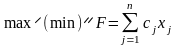 (8.1)
(8.1)
за умов:
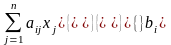
 ; (8.2)
; (8.2)
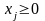
 ; (8.3)
; (8.3)
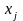 – цілі числа
.
– цілі числа
.
31. Геометрична інтерпретація задачі цілочислового програмування.
Для знаходження оптимального розв’язку цілочислових задач застосовують спеціальні методи. Найпростішим з них є знаходження оптимального розв’язку задачі як такої, що має лише неперервні змінні, з дальшим їх округленням. Такий підхід є виправданим тоді, коли змінні в оптимальному плані набувають досить великих значень у зіставленні їх з одиницями вимірювання. Нехай, наприклад, у результаті розв’язування задачі про поєднання галузей у сільськогосподарському підприємстві отримали оптимальне поголів’я корів – 1235,6. Округливши це значення до 1236, не припустимося значної похибки. Проте за деяких умов такі спрощення призводять до істотних неточностей. Скажімо, множина допустимих розв’язків деякої нецілочислової задачі лінійного програмування має вигляд, зображений на рис.8.1.
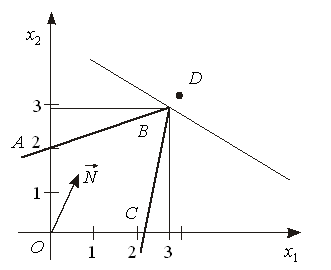
Рисунок 8.1
Максимальне
значення функціонала для даної задачі
знаходиться в точці В. Округлення
дасть таке значення оптимального плану
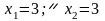 (точка D на рис.8.1). Очевидно, що
точка D не може бути розв’язком
задачі, оскільки вона навіть не належить
множині допустимих розв’язків
(чотирикутник ОАВС),
тобто відповідні значення змінних
не задовольнятимуть систему обмежень
задачі.
(точка D на рис.8.1). Очевидно, що
точка D не може бути розв’язком
задачі, оскільки вона навіть не належить
множині допустимих розв’язків
(чотирикутник ОАВС),
тобто відповідні значення змінних
не задовольнятимуть систему обмежень
задачі.
Зауважимо, що геометрично множина допустимих планів будь-якої лінійної цілочислової задачі являє собою систему точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної нецілочислової задачі. Отже, для розглянутого на рис.8.1 випадку множина допустимих планів складається з дев’яти точок (рис.8.2), які утворені перетинами сім’ї прямих, що паралельні осям Ох1 та Oх2 і проходять через точки з цілими координатами 0, 1, 2.

Рисунок 8.2
Для
знаходження цілочислового оптимального
розв’язку пряму, що відповідає цільовій
функції, пересуваємо у напрямку вектора
нормалі
до перетину з кутовою точкою утвореної
цілочислової сітки. Координати цієї
точки і є оптимальним цілочисловим
розв’язком задачі. У нашому прикладі
оптимальний цілочисловий розв’язок
відповідає точці М
( ).
).
Очевидно, особливість геометричної інтерпретації цілочислової задачі у зіставленні зі звичайною задачею лінійного програмування полягає лише у визначенні множини допустимих розв’язків. Областю допустимих розв’язків загальної задачі лінійного програмування є опуклий багатогранник, а вимога цілочисловості розв’язку приводить до такої множини допустимих розв’язків, яка є дискретною і утворюється тільки з окремих точок. Якщо у разі двох змінних розв’язок задачі можна відшукати графічним методом, тобто, використовуючи цілочислову сітку, можна досить просто знайти оптимальний план, то в іншому разі необхідно застосовувати спеціальні методи.
