
- •3.1 Появление определителей в теории слау
- •3.2 Отображения
- •3.3 Перестановки n-ой степени
- •3.4 Четные и нечетные перестановки
- •3.5 Суммирование по множеству
- •3.6 Определитель n-го порядка
- •3.7 Свойства определителя
- •3.8 Теорема Лапласа
- •3.9 Разложение определителя по элементам строки или столбца
- •Определитель произведения матриц
- •Формула обратной матрицы
- •Теорема Крамера
- •Упражнения
- •Историческая справка
- •Литература Основная литература.
- •Задачники и дополнительные методические материалы.
3.5 Суммирование по множеству
Пусть
– непустое конечное множество элементов
произвольной природы,
![]() ,
и задано произвольное отображение из
в
,
т.е. каждому элементу
из
поставлено в соответствие некоторое
действительное число
,
и задано произвольное отображение из
в
,
т.е. каждому элементу
из
поставлено в соответствие некоторое
действительное число
![]() ,
,
![]() .
.
Часто возникает необходимость в оперировании с суммой или произведением всех образов , когда пробегает множество .
На практике такая ситуация встречается постоянно. Простейшей моделью является множество предметов, загружаемых в контейнер. В этом случае в качестве отображения из в может быть рассмотрен перечень загружаемых предметов с указанием веса каждого из них, а суммой всех образов этого отображения является вес этого груза. Другим примером является зарплата коллектива работников цеха, отдела или предприятия (в качестве множества ). Отображением из в в этом случае является платежная ведомость, по которой каждый работник получает деньги в кассе.
Основной способ
введения обозначений для указанных
выше суммы и произведения (он уже
применялся выше при введении обозначений
для перестановок
-ой
степени) состоит в том, что мы, игнорируя
природу элементов множества
,
проводим их произвольную перенумерацию
от 1 до
,
вследствие чего множество
может быть заменено множеством
![]() ,
а элемент
,
а элемент
![]() этого множества – его номером
.
Тогда по определению
этого множества – его номером
.
Тогда по определению
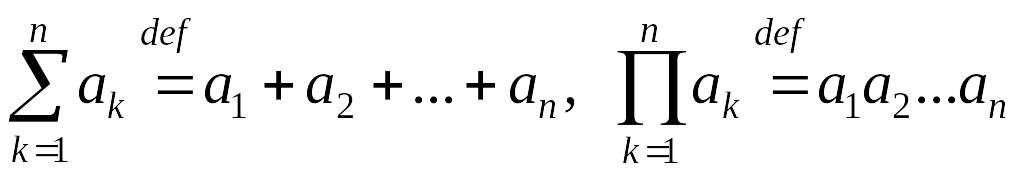 .
(3.15)
.
(3.15)
Переменный индекс , по которому идет суммирование и перемножение в левых частях равенства (3.15), называется иногда немым. Первое правило замены переменного в сумме и произведении состоит в том, что немой индекс может быть заменен на любой другой переменный индекс, например на индекс ,
 .
.
В связи с тем, что операции сложения и умножения действительных чисел обладают свойствами коммутативности и ассоциативности, порядок расположения элементов в правых частях равенства (3.15) безразличен и при его произвольном изменении значения всей суммы и всего произведения не изменяется. Иными словами, если – произвольная перестановка -ой степени, то в равенствах (3.15) справедливо следующее правило замены переменного,
 ,
,
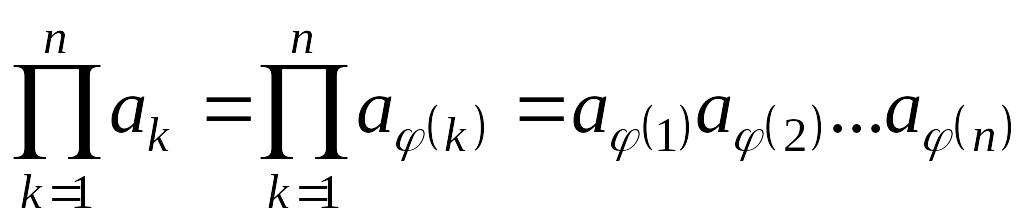 .
.
Однако, в ряде случаев игнорирования природы элементов множества доставляет определенные неудобства и при суммировании и перемножении элементов желательно в качестве индекса вместо номера сохранить его первоначальное значение . В связи с этим в качестве обозначений, эквивалентных обозначениям (3.15), применяются обозначения:
![]() , (3.16)
, (3.16)
читается: сумма по всем элементам множества , и
![]() , (3.17)
, (3.17)
читается: произведение по всем элементам множества . При этом сформулированные выше правила замены переменного в сумме и произведении вида (3.15) справедливы также для суммы (3.16) и произведения (3.17). Именно,
![]() .
.
где – произвольная перестановка элементов множества .
Лекции IX и X.
План
3.6 Определитель -го порядка.
3.7 Свойства определителя.
3.6 Определитель n-го порядка
Пусть
![]() ,
,
![]() .
Определителем
матрицы
называется действительное число
.
Определителем
матрицы
называется действительное число
![]() ,
которое вычисляется по правилу
,
которое вычисляется по правилу
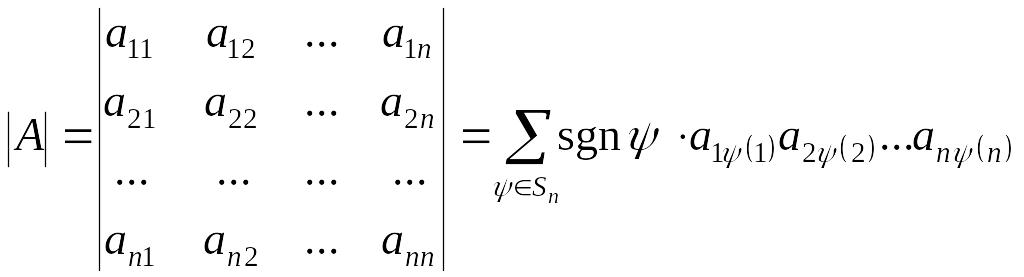 ,
(3.18)
,
(3.18)
где
 (3.19)
(3.19)
Определитель
матрицы
также называется детерминантом
матрицы
,
и в этом случае используется обозначение
![]() ,
эквивалентное обозначению
.
,
эквивалентное обозначению
.
Разберем подробно
случаи
![]() .
.
1)
![]() .
Множество
.
Множество
![]() состоит из одной единичной перестановки
состоит из одной единичной перестановки
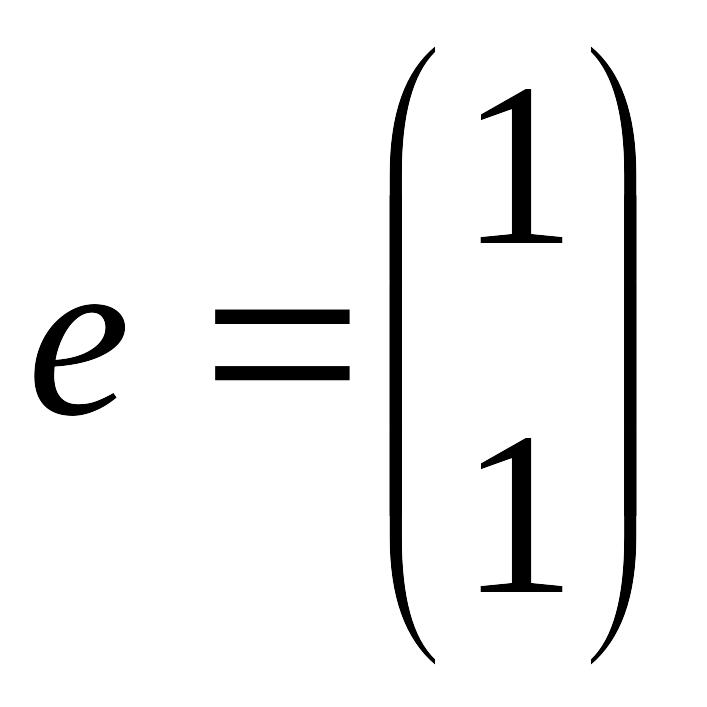 ,
которую по аналогии с единичными
перестановками более высоких степеней
естественно считать четной. Поэтому
определитель матрицы
,
которую по аналогии с единичными
перестановками более высоких степеней
естественно считать четной. Поэтому
определитель матрицы
![]() имеет вид
имеет вид
![]() .
.
2)
![]() .
Множество
.
Множество
![]() перестановок второй степени состоит
из одной четной и одной нечетной
перестановки
перестановок второй степени состоит
из одной четной и одной нечетной
перестановки
 ,
,
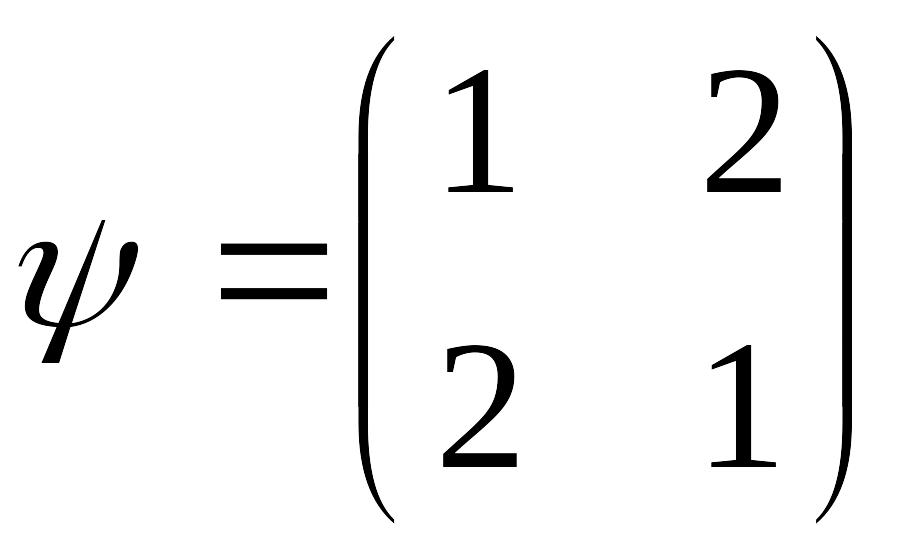 ,
,
![]() .
Поэтому сумма (3.18) имеет два слагаемых,
.
Поэтому сумма (3.18) имеет два слагаемых,
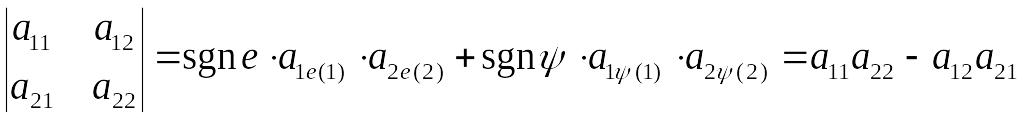 .
.
3)
![]() .
Множество
.
Множество
![]() состоит из шести перестановок третьей
степени,
состоит из шести перестановок третьей
степени,
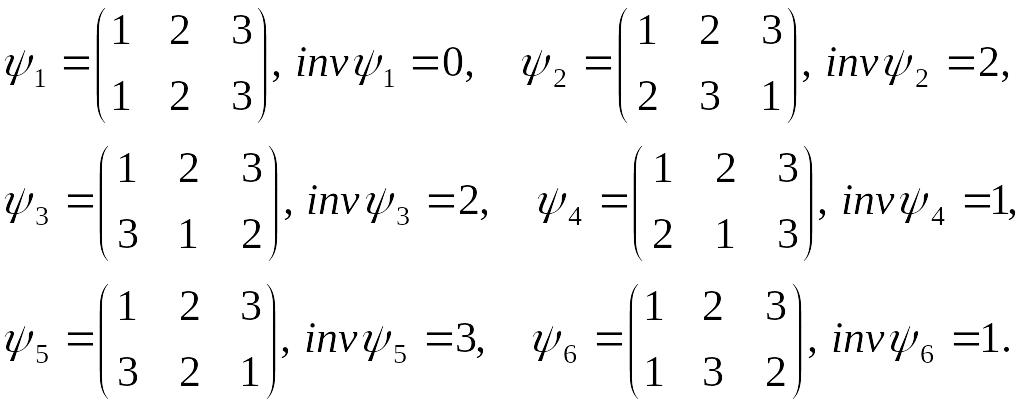
Перестановки
![]() – четные, а перестановки
– четные, а перестановки
![]() – нечетные. Поэтому
– нечетные. Поэтому

![]() . (3.20)
. (3.20)
При
![]() формула (3.18) содержит уже 24 слагаемых,
в связи с чем становится ясно, что для
вычисления определителей достаточно
высокого порядка она мало пригодна.
Нашей ближайшей задачей является
изучение таких свойств определителя,
которые бы, в частности, позволили
разработать достаточно простой способ
их вычисления, отличный от прямого счёта
по формуле (3.18). Такой способ вычисления
будет изложен ниже в пункте 3.10.
Эффективность его настолько высока,
что, как правило, этот способ целесообразно
применять даже для вычисления определителей
третьего порядка, избегая при этом
использования формулы (3.20).
формула (3.18) содержит уже 24 слагаемых,
в связи с чем становится ясно, что для
вычисления определителей достаточно
высокого порядка она мало пригодна.
Нашей ближайшей задачей является
изучение таких свойств определителя,
которые бы, в частности, позволили
разработать достаточно простой способ
их вычисления, отличный от прямого счёта
по формуле (3.18). Такой способ вычисления
будет изложен ниже в пункте 3.10.
Эффективность его настолько высока,
что, как правило, этот способ целесообразно
применять даже для вычисления определителей
третьего порядка, избегая при этом
использования формулы (3.20).
Принимая во внимание
запись определителя
![]() в виде таблицы (3.18), ниже будем использовать
следующие термины с очевидным их
содержанием: определитель порядка
,
элемент определителя, строка определителя,
столбец определителя.
в виде таблицы (3.18), ниже будем использовать
следующие термины с очевидным их
содержанием: определитель порядка
,
элемент определителя, строка определителя,
столбец определителя.
