2.6. Теорій масового обслуговування

При аналізі економічних систем часто зустрічається специфічний клас завдань, що відносяться до масового обслуговування. Спочатку методи теорії масового обслуговування використовувалися для вирішення тільки питань зв'язку, а потім були поширені на побутове обслуговування, військову справу, охорону здоров'я, дослідження динаміки функціонування достатньо складних систем, технологічних потоків ремонту, контролю і інших виробничих процесів.

Система масового обслуговування характеризується структурою, яка визначається складом і функціональними зв'язками. Вона складається з наступних елементів: вхідний потік вимог, черга вимог, чекаючих обслуговування, прилади (канали) обслуговування і потік вимог, що виходить.

Ця схема може бути ускладнена, якщо система складається з ряду послідовних приладів, з ряду послідовно і паралельно зв'язаних приладів або має ще складнішу мережеву структуру. Загальною особливістю всіх завдань, пов'язаних з масовим обслуговуванням, є випадковий характер досліджуваних явищ. Кількість вимог на обслуговування і тимчасові інтервали між їх надходженнями, тривалість обслуговування вимог випадкові. Час перебування вимог в деяких видах систем масового обслуговування також випадково.

Вхідним потоком є сукупність вимог, які поступають в систему і потребують обслуговування. Процес надходження в систему масового обслуговування потоку вимог є імовірнісним і представляє потік подій, які наступають через випадкові проміжки часу. Прикладами вхідних потоків можуть бути потік інформації, що поступає на обробку в ЕОМ; поділа, що направляються в організацію, хворі, що поступають в лікарню, і так далі. По числу каналів обслуговування системи діляться на одноканальних і багатоканальних. Прикладом одноканальної системи може служити одиночний пункт відділу технічного контролю (ОТК) на потоці, перукарня з одним майстром і тому подібне Звичайне число каналів в багатоканальних системах обмежено, хоча іноді їх буває так багато, що вигідніше для аналізу ці системи вважати такими, що мають нескінченне число каналів. Разом з тим і багатоканальні системи можуть складатися з однакових і різних каналів і відрізнятися продуктивністю при обслуговуванні.

Для оцінки якості роботи систем масового обслуговування приймаються критерії хорошої організації обслуговування (задоволення заявок), завантаженості каналів (чи не створюється велика черга, чи не великий відхід з системи необслужених вимог і так далі). Системи можуть бути неполнодоступными і повнодоступними залежно від того, чи можливо для кожної вимоги поступити на обслуговування будь-якого каналу системи.

Вимоги потоку можуть бути обслужені приладами системи і не обслужені. Потік, що виходить, - потік вимог, що покидають систему. Дослідження структури потоку, що виходить, має велике значення, оскільки він може бути вхідним потоком для іншої групи приладів. Розподілите вимог в потоці, що виходить, в часі залежить від щільності вхідного потоку і характеристик роботи приладів обслуговування системи.

Основним завданням масового обслуговування є визначення кількісних показників функціонування 'систем масового обслуговування і їх залежності від параметрів вхідного потоку і структури самої системи. Рішення цієї задачі дає можливість знайти в системі слабкі ланки, визначити їх вплив на ефективність обслуговування і знайти шляхи їх поліпшення або при заданих характеристиках потоку вимог і критеріїв якості обслуговування дати пропозиції про структуру системи, яка забезпечить поставлені перед нею завдання. Для цього на другому етапі можуть бути привернуті різні методи оптимізації: лінійне і нелінійне програмування, динамічне програмування, теорія ігор і ін.

Потік вимог, що поступає на вхід системи масового обслуговування, можна вважати потоком випадкових подій, оскільки моменти надходження вимог заздалегідь невідомі. Випадкові тимчасові інтервали між надходженнями подій в потоці можуть підкорятися різним законам розподілу. Проте в переважній більшості робіт по теорії масового обслуговування розглядається пуассоновский (простий) потік, в якому вірогідність надходження k вимог в проміжок часу t задається формулою Пуассона

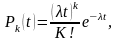
де λ >0— щільність потоку; λt = а -математическое очікування числа подій ш ділянці t [15, 16].

Це пояснюється тим, що для інших видів потоків важко отримати аналітичні залежності для кількісної оцінки якості функціонування систем масового обслуговування. Разом з тим показано в роботі [17], що у ряді випадків розрахунок системи в припущенні пуассоновского характеру вхідного потоку дає оцінки ефективності з «запасом», якщо насправді потік має інший характер. Нарешті, простий шток в теорії масового обслуговування грає таку ж роль, як нормальний закон розподілу випадкових величин в теорії вірогідності. При складанні великого числа мало інтенсивних випадкових потоків утворюється сумарний потік, близький по своїх характеристиках до

простого. Простий потік володіє трьома основними властивостями: стаціонарністю, ординарністю і відсутністю післядії.

Потік подій називається стаціонарним, якщо вірогідність попадання якогось числа подій на певну ділянку часу залежить тільки, від довжини цієї ділянки і не залежить від того, де на осі часу розташована дана ділянка. Для стаціонарного потоку характерна незалежність імовірнісних характеристик від часу, він має постійну щільність (середнє число вимог в одиницю часу).

Потік подій називається ординарним, якщо вірогідність попадання на елементарну ділянку Δt два і більш за події є величина більшого порядку трохи в порівнянні з вірогідністю попадання однієї події на цю ділянку. Таким чином, ординарність потоку вимог означає практичну неможливість появи два і більш за вимоги в один і той же момент часу.

Потік подій називається потоком без післядії, якщо для будь-яких ділянок часу, що не перекриваються, число подій, що потрапляють на один з них, не залежить від числа подій, що потрапляють на інших. Це означає, що вимоги поступають в систему незалежно один від одного.

Важливою характеристикою потоку є його інтенсивність, яка визначається як математичне очікування числа вимог, що поступають на одиницю часу. Оскільки математичне очікування числа вимог, що поступають за проміжок часу t, складає

то інтенсивність (що виходить при t = 1) визначається як М₁ (k)=λ.

У багатьох завданнях припущення про стаціонарність потоку свідомо помилково. Такі потоки називаються нестаціонарними простими потоками. Для цих потоків практичні завдання вирішуються за допомогою моделювання системи масового обслуговування на аналогових або цифрових ЕОМ. Для наближених розрахунків слідує весь інтервал часу розбити на періоди, в межах яких можна припустити з деякою погрішністю стаціонарність потоку.

Поширеною математичною моделлю для аналізу ряду систем масового обслуговування більш загальною, ніж простий потік, є рекурентний вхідний потік. Рекурентним називається будь-який потік, в якому інтервали часу між послідовними подіями є незалежними. Для розгляду таких потоків при моделюванні реальних систем масового обслуговування необхідно досліджувати на незалежність тимчасові інтервали між вимогами. При цьому можна скористатися визначенням вибіркового коефіцієнта кореляції:

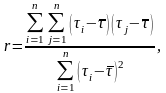
де 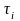тимчасові проміжки між послідовними вимогами, що поступають, в систему масового обслуговування; 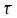- вибіркове середнє величин .

Якщо величина r багато менше одиниці, то випадкові величини можна вважати взаємно незалежними.

У аналіз реальних потоків повинна також входити оцінка параметрів і розподілу вхідного потоку. Для цього вибирається період часу, протягом якого потік є практично стаціонарним. Даний відрізок делитгея на ряд тимчасових інтервалів, в межах яких підраховуються вимоги, що поступили, і будується гістограма частот. За допомогою будь-якого критерію згоди (наприклад, x²) отриманий статистичекое розподіл порівнюється з теоретичним. Як приклад розглянемо перевірку гіпотези про пуассоновском розподіл вхідного потоку.

Спостережуваний період часу розділимо на 100 двохвилинних інтервалів, в кожному з яких визначимо число події. Після цього згрупуємо інтервали з однаковим числом подій. Результати приведені в табл. 2.3.

Таблиця 2.3

Число подій ai у інтервалі u=2хв	Число інтервалів з однаковим числом подій ni	Пуассонiвський розподіл	Математичне очікування числа інтервалів пT	Число подій ai у інтервалі u=2хв	Число інтервалів з однаковим числом подій пi	Пуассонiвський розподіл	Математичне очікування числа інтервалів пT
1	2	3	4	1	2	3	4
0	0	0,010	1	8	4	0,050	5,0
1	5	0,046	4,6	9	2	0,026	2,6
2	11	0,106	10,6	10	1	0,012	1,2
3	13	0,163	16,3	11	1	0,005	0,5
4	22	0,187	18,7	12	0	0,002	0,2
5	18	0,172	17,2	13	0	0,002	0,2
6	14	0,132	13,2	Сумма	100	1.000	100,0
7	9	0,087	8,7

Визначимо математичне очікування числа подій протягом інтервалу t = 2 хв:

За значенням 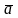= 4,6 в гр. 3 вносимо вірогідність числа подій при пуассонівскому розподілі, а в гр. 4-математичне очікування числа інтервалів, протягом якого відбулося число подій. Розглянемо величину

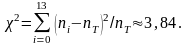
Для оцінки відповідності отриманого експериментального розподілу теоретичному скористаємося таблицями 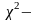розподілу з числом мір свободи, рівним 12 (числу інтервалів без двох). З таблиць розподілу визначаємо вірогідність Р того, що експериментальний розподіл є пуассонівским: Р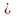 0,99. Це говорить про відповідність експериментального розподілу пуассонівскому.

Найбільш широкого поширення набула класифікація систем масового обслуговування за часом перебування вимог в системі до початку обслуговування. При цьому всі системи розбиваються на три групи; з відмовами, з необмеженим часом очікування і змішаного типу.

Вимога, що поступає в систему з відмовами, у разі зайнятості каналів обслуговування покидає її. Класичним прикладом систем з відмовами може служити робота автоматичної телефонної станції. У системах з необмеженим часом очікування вимог вимога, що поступила, вимушена чекати своєї черги, поки не звільниться один з каналів. Ці системи мають широке застосування з практиці. Системи змішаного типу обмежують час перебування вимоги в черзі, після чого необслужена вимога покидає систему. Прикладом такої системи можуть служити пункти переробки і продажу фруктів, овочів, які можуть зберігатися обмежений час. Також може бути обмежене час на перебування вимоги в системі, обмежена довжина черги. Системи можуть розрізнятися і по порядку обслуговування вимог, що поступили в них, тобто в строгому порядку, випадково і так далі.

Найважливішою характеристикою кожного каналу обслуговування системи є час обслуговування, що визначає пропускну спроможність системи. Як правило, час обслуговування є випадковим величиною, оскільки завжди має місце нестабільність роботи приладів обслуговування, неідентичність вимог, що поступають в систему. Повною характеристикою цієї випадкової величини є закон розподілу

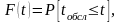
де 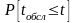- вірогідність того, що час обслуговування 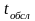не перевершує деякої величини t.

Вважається, що F(t)= 0 при t ≤ 0. Закон розподілу часу обслуговування визначається з досвіду шляхом статистичних методів аналізу чисельних значень часу обслуговування реальних систем. Оцінки розподілу часу обслуговування реальних систем нічим не відрізняються від оцінок вхідного потоку. Закони розподілу можуть бути самого різного вигляду, але як в практичних, так і в теоретичних дослідженнях найбільшого поширення набув показовий закон. Це пов'язано з тим, що при показовому законі розподілу значно спрощуються всі результати, а для довільного закону розподілу часу розробка методів вирішення завдань масового обслуговування зустрічає великі труднощі.

При показовому законі функція розподілу має вигляд

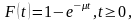
де 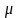= 1/ >0, - середній час обслуговування вимоги, математичне очікування часу обслуговування.

Показовий закон часу обслуговування припускає, що значна частка вимог обслуговуватиметься швидко. Це не завжди відповідає практиці, тому А. К. Ерланг запропонував щільність розподілу часу обслуговування задавати формулою

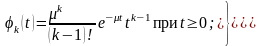
Можна показати, що φ_k(t) є щільністю розподілу суми k незалежних випадкових величин з показовим законом розподілу.

Велике значення має дослідження характеристик потоку, що виходить, особливо якщо він сам є вхідним потоком для інших систем, розташованих послідовно з попередньою. Для таких систем часто виникає питання про вплив наявності післядії в потоці вимог на вірогідність відмови, оскільки якщо вхідний потік є простим, то потік, що виходить, з цієї системи не завжди буде простим, йому властиво післядія.

Під ефективністю обслуговуючої системи розуміють характеристику рівня виконання цією системою тих функцій, для яких вона призначена. Вибір показника ефективності залежить від того завдання, яке поставлене перед дослідженням.

Зазвичай при вирішенні економічних завдань потрібно досягти екстремального значення деякого критерію (функції вартості), визначуваного для різних конкретних умов. При дослідженні роботи систем масового обслуговування зазвичай мінімізуються витрати із-за простою і очікування, втрати унаслідок відходу вимоги без обслуговування; визначається доцільність збільшення числа каналів. Математичні методи теорії масового обслуговування дають можливість знайти середнє число вимог, що знаходяться в системі (у черзі), середнє число необслужених вимог, середній час очікування, вірогідність відмови, вірогідність того, що довжина черги не перевищить задану, і так далі Всі пропоновані показники характеризують здібність системи до обслуговування вимог, зовсім не визначаючи якості самого обслуговування.

Найбільш часто вживані показники ефективності функціонування Систем масового обслуговування [18] наступні.

1. Вірогідність втрати вимоги в системі масового обслуговування р_отк. Стосовно систем масового обслуговування без накопичувача ця характеристика рівна вірогідності р_п зайнятості обслуговуванням вимог всіх п приладів системи.

2 Вірогідність р_k того, що обслуговуванням вимог в системі зайнято k приладів. Це якнайповніша характеристика, окремим випадком якої є р_п (р₀ – вірогідність того, що всі прилади вільні).

3. Середнє число зайнятих приладів (каналів, ліній), що характеризує ступінь завантаження обслуговуваної системи,

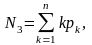
де р_k - вірогідність того, що в системі знаходиться k вимог.

4. Середнє число вільних від обслуговування приладів

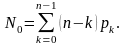
5. Коефіцієнт простою приладів (каналів, ліній) системи обслуговування як похідний від показника N₀ : k_пр = N₀/n.

6. Коефіцієнт зайнятості устаткування, приладів, системи k_з = N_з/n.

7. Закон розподілу часу очікування в черзі для систем з очікуванням, тобто 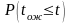. На практиці найчастіше обмежуються визначенням середнього часу очікування в черзі:

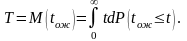
8. Середня довжина черги для систем з очікуванням

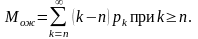
9. Середнє число вимог (заявок), що знаходяться у сфері обслуговування:

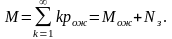
10. Вірогідність того, що число вимог (заявок) в системі, чекаючих початку обслуговування, більше деякого числа

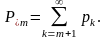
Цей показник особливо необхідний при оцінці можливостей розміщення вимог при обмеженості часу для очікування.

Окрім перерахованих критеріїв при оцінці ефективності систем масового обслуговування можуть бути використані вартісні показники: q_0б- вартість обслуговування кожної вимоги в системі; q_ож- вартість втрат, пов'язаних з простоєм вимог в черзі в одиницю часу; вартість збитків, пов'язаних з відходом з системи необслужених вимог; q_y- вартість експлуатації кожного приладу системи в одиницю часу; q_{п. к}- вартість одиниці часу простою приладу системи.

При виборі оптимальних параметрів систем масового обслуговування за економічними показниками часто використовується функція вартості втрат в системі:

де T-інтервал часу.

У інших випадках можуть бути вибрані інші критерії. Так, при вирішенні деяких завдань доцільно користуватися критерієм економічної ефективності системи масового обслуговування

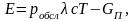
де - ймовірність обслуговування вимоги (заявки); с - економічний ефект, отриманий при обслуговуванні кожної вимоги.

Розглянемо одноканальну систему з очікуванням і показовим часом обслуговування, на вхід якої поступає простий потік вимог [14]. Покажемо, як в цьому випадку визначити функцію вартості втрат G_п. Очевидно, що в цьому випадку п= 1, N₀ рівно вірогідності того, що в системі немає жодної вимоги.

Стан системи в деякий момент часу визначається числом вимог, що знаходяться в ній k. Позначимо через А_k стан, при якому в системі знаходяться k вимог; у інтервалі (t, t +Δt), де Δt малe, можуть відбутися наступні переходи:

де k ≥ 1.

Такий перехід, як наприклад, 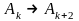, матиме вірогідність другого порядку трохи в порівнянні з Δt.

Хай р_к(t) - вірогідність стану А_k у момент t; λΔt - вірогідність надходження вимоги в інтервалі Δt; μΔt - вірогідність закінчення обслуговування в цьому інтервалі.

В цьому випадку (при k ≥ 1) маємо

Зміни стану

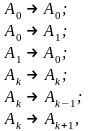
Вірогідність переходу

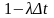
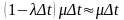
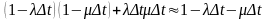
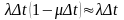
Матриця переходу з точністю до Δt має вигляд

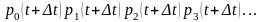
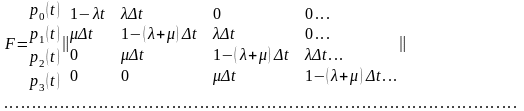
Якщо покласти р(t) = [p₀(t), p₁(t), …, p_k(t)], тоді рівняння станів системи буде p(t+Δt) = р(t)F.

Звідси p(t+Δt) = (1-λΔt)p₀(t) + μΔtp₁(t); p_k(t+Δt) = λΔtp_k-1(t) + (1 – λΔt)p_k(t) + μΔtp_k+1(t), k ≥ 0.

Розділивши отримані вирази на Δt, наблизивши Δt до нуля, отримаємо диференціальні рівняння станів системи масового обслуговування:

(2.22)

Початкові умови записуються у вигляд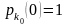і і , .

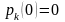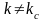Вирішення системи рівнянь (2.22) за заданих початкових умов в загальному вигляді досить громіздко. Припустимо, що при 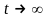режим в системі встановлюється і все р_k = const. Тоді для них справедливі рівняння

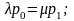
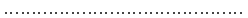
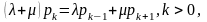
з яких виходить

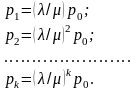
В той же час

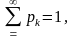
тому

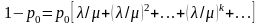
або

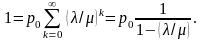(2.23)

Позначивши 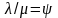, отримаємо.

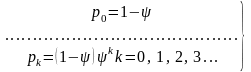(2.24)

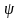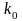Для збіжності (2.23) необхідно, щоб < 1. Відомо, що цю ж умову забезпечує існування самого сталого режиму. Величина називається коефіцієнтом використання системи. У приведеному виводі не бере участь початкове число вимог , що знаходяться в системі. Тому при зроблених припущеннях сталий режим не залежить від початкових умов.

Вірогідність того, що випадкова величина N, що є числом вимог в системі, перевершить k, обчислюється за формулою

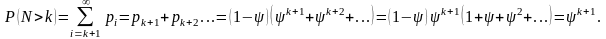
B частковості, вірогідність того, що в системі є хоч би одна вимога, складе

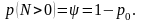
Цей же результат можна отримати і з виразу (2.24). Середнє число вимог в системі

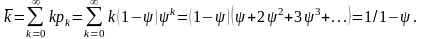
Середня довжина черги

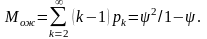
З урахуванням цього можна записати

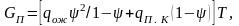
оскільки N₀ = р₀ = 1 — ψ.

Таким чином, знаючи витрати, пов'язані з очікуванням, простоєм і обслуговуванням, можна для даного потоку визначити витрати в конкретній системі масового обслуговування за певний інтервал часу.

Змінивши число каналів і, параметр обслуговування μ, технічну надійність системи, можна набути екстремального значення вибраного критерію в конкретних умовах. Хай є ремонтна майстерня при якій-небудь лабораторії, поновлююча інструменти, що вийшли з ладу, прилади і так далі. Припустимо, що потік вимог (несправних одиниць) простий, а час обслуговування показовий. 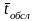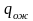Хай в середньому за робочий день поступають 28 несправних одиниць, середній час обслуговування = 12 хв, = 0,5 руб/ч на кожну вимогу 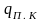= 1 руб/ч.

Маємо також λ = 28/7 = 4 вимог/год; μ = 1/ = 1/0,2 = 5 вимог/год, тобто ψ = λ/μ = 4/5 = 0,8. Отже, М_ож = ψ²/(1 — ψ) = 0,82/0,2 = 3,2. Отже, середня довжина черги складає 3,2 вимог, вірогідність простою складе р₀ = 1 — ψ = 0,2. Витрати за місяць будуть G_П = (0,5 • 3,2 + + 1-0,2)7 · 25 = 315 р.

Визначимо, як змінюються витрати, пов'язані з очікуванням і простоєм після технологічного переобладнання майстерні, в результаті якого середній час обслуговування скоротився на 2,4 хв, тобто знайдемо змінене М_ож= Р₀ :

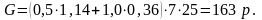
Отже, витрати знизилися на 152 р. в місяць.

Аналітичні методи, використовувані в теорії масового обслуговування, дають можливість досліджувати велике число теоретичних завдань, багато хто з яких часто зустрічається па практиці. Проте прикладні завдання нерідко виявляються набагато складнішими. У них розглядаються послідовні і паралельні з'єднання систем, нестаціонарні процеси, детерміновані або імовірнісні зворотні зв'язки і так далі У таких випадках доцільно досліджувати системи масового обслуговування за допомогою моделювання. Дуже часто на практиці застосовується метод статистичних випробувань.

Не слід протиставляти аналітичні методи методам моделювання, вони розвиваються спільно або часто зв'язані один з одним. Так, моделювання може спиратися на математичну модель, а експеримент часто дозволяє удосконалити математичну модель процесу. Це має місце як для масового обслуговування, так і для дослідження інших фізичних явищ і процесів. Методи моделювання набули широкого поширення з появою ЕОМ, що мають високу продуктивність і що володіють великим об'ємом оперативної пам'яті, і стали необхідними для дослідження практичних завдань.