
- •Исключение бесполезных символов
- •Исключение бесполезных символов
- •Исключение -правил
- •Исключение -правил
- •Исключение цепных правил
- •Исключение цепных правил
- •Исключение цепных правил
- •Исключение левой рекурсии
- •Исключение левой рекурсии
- •Граф переходов полученного детерминированного автомата
- •Функции переходов
- •Описание языка, допускаемого конечным автоматом
- •Построение детерминированного конечного автомата по автоматной грамматике
- •Построение детерминированного конечного автомата по автоматной грамматике
- •Построение детерминированного конечного преобразователя
- •Построение детерминированного конечного преобразователя
- •Построение детерминированного автомата (распознаватель) с магазинной памятью Формулировка задания
- •Функции переходов:
- •Построение детерминированного автомата (распознаватель) с магазинной памятью
- •Построение детерминированного преобразователя с магазинной памятью.
- •Построение детерминированного преобразователя с магазинной памятью.
- •Построение недетерминированного расширенного мп-автомата по кс-грамматике
- •Построение недетерминированного расширенного мп-автомата по кс-грамматике
- •Формулировка задания
- •Задание
- •Решение
- •Формулировка задания
- •Задание
- •Построение управляющей таблицы
- •Формулировка задания:
- •Пример разбора цепочки, порождаемой заданной грамматикой предшествования
Искючим из грамматики правила, содержащие непроизводящие нетерминалы
R’={ S ® b, S ® C, A ® e, A ® Ab, C ® Ca, C ® d }
G1=( T, Np, S, R’)
Множество достижимых символов Nr = {d,a,b,S,C}
N0={S}
N1={S,b,C}, из правил S ® b, S ® C
N2={S,b,C,a,d} из правил C ® Ca, C ® d
N3={S,C,b,a,d}.
Nr = {d,a,b,S,C}
Исходная грамматика без бесполезных символов будет выглядеть следующим образом.
N’={S,C}, T’={a, b, d}, R’’={ S ® b, S ® C, C ® Ca, C ® d }
G = < T’, N’, S, R’’ >
Исключение -правил
Алгоритм 3.7.2.1. Построение множества укорачивающих нетерминалов.
Вход. КС-грамматика G = (, , P, S).
Выход. Множество укорачивающих нетерминалов: = {A | A + , A }.
Описание алгоритма.
Построить рекурсивно множества укорачивающих нетерминалов 0, 1, … , i, … , следующим образом:
Положить 0 = {A | A , A }, i = 1.
Положить i = i-1 {A | A P и (i-1)+}.
Если i i-1, положить i = i + 1 и перейти к шагу 2.
Положить = i.
Конец алгоритма
Так как , число повторений шага 2 алгоритма не превышает n + 1, где n – число нетерминалов грамматики G.
Замечание
При определении множеств i можно рассматривать только правила вывода, не содержащие в правых частях терминалы.
Алгоритм 3.7.2.2. Преобразование КС-грамматики с -правилами в эквивалентную НКС-грамматику.
Вход. КС-грамматика G = (, , P, S).
Выход. НКС-грамматика G¢ = (¢, , P¢, S¢), порождающая язык L(G¢) = L(G).
Описание алгоритма.
Построить множество укорачивающих нетерминалов.
Построить P¢ следующим образом:
Положить P¢ = .
Если A 0B11B22… Bkk P, где k 0, Bj (1 j k) и ни один из символов цепочек i ( )* (0 i k) не содержит символов из , то включить в P¢ все правила вывода вида A 0X11X22… Xkk, где Xj = Bj или X = . Если все цепочки i = , то правило A не включать в P¢.
Если S , то положить ¢ = {S¢} и добавить в P¢ два правила: S¢ S и S¢ , в противном случае ¢ = и S¢ = S.
Положить G¢ = (¢, , P¢, S¢).
Конец алгоритма
Пример 3.8
Преобразовать КС-грамматику G = (, , P, S). где = {А, S}, = {b, c}, P = {S сА, S , А сA, А bA, A }, в эквивалентную НКС-грамматику.
Используя алгоритм 3.7.2.1, получаем: 0 = {S, A}, 1 = {S, A}, значит = 1 = {S, A}.
Далее, выполняя шаги алгоритма 3.7.2.2, имеем:
Шаг 1. P¢ = .
Шаг 2. Рассмотрим правило S сА. Для него в новое множество правил грамматики P¢ нужно включить правила S сA и S с. Для правила А à сA требуется добавить в множество P¢ правила А à сA и А à с, а для правила А à bA – правила А à bA и А à b. На данном шаге алгоритма получаем P¢ = {S à сА, S à с, А à сA, А à с, А à bA, А à b}
Шаг 3. В рассматриваемой грамматике S , поэтому в множество нетерминальных символов добавляем новый нетерминал S¢, а в множество правил P¢ — два правила: S¢ S и S¢ .
Окончательно имеем НКС-грамматику G¢ = ({S¢, S, A}, {b, c}, {S¢ S, S¢ , S à сА, S à с, А à сA, А à с, А à bA, А à b }, S¢), которая эквивалентна исходной грамматике.
Исключение -правил
Формулировка задания
Преобразовать исходную КС-грамматику G = <T, N, S, R> в эквивалентную НКС-грамматику.
Задание.
2.2.2.3 T = { a, b, c, d }, N = { S, A, B }, R = { S Aa, S bB, A cAdA, A a, A , B ®cBdd, B ®};
Решение:
Построим множество укорачивающих нетерминалов.

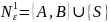
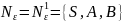
Преобразуем исходную КС-грамматику с -правилами в эквивалентную НКС-грамматику.
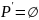
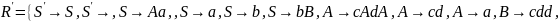

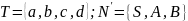
Новая грамматика, эквивалентная исходной имеет следующий вид:
G’ = <T, N’, S’, R’ >
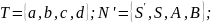 ;
;
Исключение -правил
Преобразовать исходную КС-грамматику G = < T, N, S, R > в эквивалентную НКС-грамматику:
2.2.2.1. T = { a, b }, N = { A, B, S }, R = { S AB, A SA, A BB, A bB, B b, B aA, B };
Множество укорачивающих нетерминалов:
Nε ={B, A, S}
N0={B} из правила B
N1={B,A} из правила A BB
N2={B,A,S} из правила S AB
Nε ={B, A, S}
Построение R’ = {
B b,
B aA,
B a, //A Nε, исключаем правило A BB,
A bB,
A b, //B Nε, исключаем правило B
A SA,
A S, //S Nε, исключаем правило S AB
S AB,
S A,
S B,
S’ S, //S Nε ,добавляем правило S’
S’
}
Т.о.преобразованная грамматика -
G’ = < T, N, S’, R’ >
Исключение -правил
Преобразовать исходную КС-грамматику G = < T, N, S, R > в эквивалентную НКС-грамматику:
2.2.2.1. T = { a, b }, N = { A, B, S }, R = { S ® AB, A ® SA, A ® BB, A ® bB, B ® b, B ® aA, B ® e};
Множество укорачивающих нетерминалов:
Nε ={B, A, S}
N0={B} из правила B ® e
N1={B,A} из правила A ® BB
N2={B,A,S} из правила S ® AB
Nε ={B, A, S}
Построение R’ = {
B ® b,
B ® aA,
B ® a, //AÎ Nε, исключаем правило A ® BB,
A ® bB,
A ® b, //BÎ Nε, исключаем правило B ® e
A ® SA,
A ® S, //SÎ Nε, исключаем правило S ® AB
S ® AB,
S ® A,
S ® B,
S’ ® S, //SÎ Nε ,добавляем правило S’ ® e
S’ ® e
}
Т.о.преобразованная грамматика -
G’ = < T, N, S’, R’ >
Исключение цепных правил
Определение. Правило вывода вида А В называется цепным правилом.
Алгоритм 3.7.3. Исключение цепных правил.
Вход. НКС-грамматика G = (, , P, S).
Выход. Эквивалентная НКС-грамматика G¢ = (, , P¢, S) без цепных правил.
Описание алгоритма.
Для каждого A построить множество A = {B | A * B}следующим образом:
Положить 0A = {A} и i = 1.
Положить iA = i-1A {C | B C P и B i-1A}.
Если iA i-1A, то положить A = iA.
Положить P¢ = .
Если B P и не является цепным правилом, положить P¢ = P¢ {A } для всех таких A, что B A.
Положить G¢ = (, , P¢, S).
Конец алгоритма
Пример 3.9
Исключить цепные правила из КС-грамматики G0 с правилами P:
-
(1)
E
E + T
(2)
E
T
(3)
T
T*P
(4)
T
P
(5)
P
i
(6)
P
(E)
Шаг 1. После выполнения шага 1 алгоритма получим: E = {E, T, P}, T = {T, P}, P = {P}.
Шаг 2. P¢ = .
Шаг 3. Выберем первый нетерминал E из множества NE. Формируя множество правил, левая часть которых – нетерминальный символ E, а правые части – это правые части нецепных правил исходной грамматики, в левой части которых находятся символы из множества NE, получаем: {E à E + T, E à T * P, E à (E), E à i}. Включаем эти правила в P¢ и имеем P¢= {E à E + T, E à T * P, E à (E), E à i}. Таким же образом рассматриваем остальные символы из NE , затем символы множеств NT и NP. Окончательно получаем G¢ = (N, S, P¢, S), где P¢ = {E E + T, E T * P, E i, E (E), T T * P, T (E), T i, P (E), P i}.
Исключение цепных правил
Формулировка задания
Преобразовать НКС-грамматику G = <T, N, S, R> в эквивалентную КС-грамматику, не содержащую цепных правил.
Задание.
 /
/
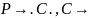 /
/
Решение:
Для каждого нетерминального символа построим множество



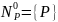

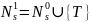
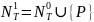
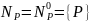
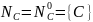


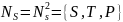
Исключим цепные правила
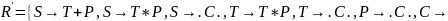 /
/
Новая грамматика, эквивалентная исходной имеет следующий вид:
G’ = <T, N, S, R’ >
/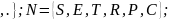
/
Исключение цепных правил
Преобразовать НКС-грамматику G = < T, N, S, R > в эквивалентную КС-грамматику, не содержащую цепных правил.
2.2.3.1. T = { i, :=, (, ) }, N = { S, A, B, F, L, P, Q }, R = { S LA, S LB, L P:= , L Q:= , P i, A F, Q i, B F, F Q(i) };
1. для каждого D из N построим множество ND {E | D * E}
NS={S} NA={A,F} NB{B,F} NF={F} NL={L} NP={P} NQ={Q}
2. Построим R’ без цепных правил
wR’ = {S LA, S LB, L P:= , L Q:= , P i, Q i, AQ(i), BQ(i)}, FQ(i)};
Т.о. преобразованная грамматика –
G = < T, N, S, R’ >
Исключение цепных правил
Преобразовать НКС-грамматику G = < T, N, S, R > в эквивалентную КС-грамматику, не содержащую цепных правил.
2.2.3.1. T = { i, :=, (, ) }, N = { S, A, B, F, L, P, Q }, R = { S ® LA, S ® LB, L ® P:= , L ® Q:= , P ® i, A ® F, Q ® i, B ® F, F ® Q(i) };
1. для каждого D из N построим множество ND {E | D ® * E}
NS={S} NA={A,F} NB{B,F} NF={F} NL={L} NP={P} NQ={Q}
2. Построим R’ без цепных правил
wR’ = {S ®LA, S ® LB, L ® P:= , L ® Q:= , P ® i, Q ® i, A®Q(i), B®Q(i)}, F®Q(i)};
Исключение левой рекурсии
Алгоритм 3.7.5. Устранение прямой левой рекурсии.
Вход. Приведенная КС-грамматика G = (, , P, S).
Выход. Эквивалентная КС-грамматика G¢ = (¢, , P¢, S) без левой рекурсии.
Описание алгоритма.
Пусть множество нетерминалов грамматики = {A1, A2, … , An}. Преобразуем грамматику таким образом, чтобы в правиле Ai цепочка начиналась либо с терминала, либо с такого Aj, что j > i. Установим i = 1.
Пусть множество Ai-правил имеет вид Ai Ai1, Ai Ai2, …, Ai Aim Ai 1, Ai 2, …, Ai m, где ни одна из цепочек j, не начинается с Ak, если k i. Заменим Ai-правила правилами Ai 1, Ai 2, …, Ai n, Ai 1A¢i, Ai 2A¢I, …, Ai n A¢i и Ai¢à a1, Ai¢à a2, …, Ai¢ à am, Ai¢à a1A¢i, Ai¢ à a2A¢i, …, Ai¢à amA¢i, где A¢i – новый нетерминальный символ. После выполнения такой замены правые части всех Ai-правил начинаются с терминального символа или с нетерминала Ak, для некоторого k > i.
Если i = n, то преобразование завершено, иначе положить i = i + l и j = l.
Заменить каждое правило Ai Aj правилами Ai 1, Ai 2, …, Ai m, где Aj 1, Aj 2, …, Aj m – все Aj-правила грамматики. Правая часть Aj – правила начинается с терминального символа или с нетерминала Ak для k > j, поэтому правая часть каждого построенного Ai – правила обладает этим же свойством.
Если j = i – 1, то перейти к шагу 2 алгоритма, иначе положить j = j + 1 и перейти к шагу 4.
Конец алгоритма
Пример 3.11
Исключить левую рекурсию из грамматики G0 с правилами
-
(1)
E
E + T
(2)
E
T
(3)
T
T*P
(4)
T
P
(5)
P
i
(6)
P
(E)
Применив к E-правилам E E+T , E T описанное преобразование, получим = +T и = T. В соответствии с этим преобразованием, новые E-правила будут иметь вид: E T, E TE¢ и в грамматику необходимо добавить правило для нового нетерминала E¢: E¢ +T.
После рассмотрения всех правил исходной грамматики G получим правила новой грамматики G¢:
E T, E TE¢, E¢ +T, E¢ +TE¢, T P, T PT¢, T¢ *P, T¢ *PT¢, P (E+T), P (E), P i.
Пример 3.12
Устраним левую рекурсию в грамматике G, определяемой множеством правил P = {S AB, S a, A BS, A Sb, B SA, B BB, B a}.
Положим А1 = S, А2 = A и А3 = B и выполним алгоритм 3.7.5 по шагам.
Шаг 1. i = 1.
Шаг 2. Правила вывода вида A1 A1 (в обозначениях исходной грамматики S S) в грамматике нет. Шаг не выполняется.
Шаг 3. i = 2, j = 1.
Шаг 4. Найдем все правила вида A2 A1 (для нашего примера — это A S). Таких правил в грамматике только одно — это правило A Sb. Для выполнения замены этого правила нужно найти правила, в правой части которых стоит символ A1 (т.е. S).
После замены правила A Sb получим новое множество правил P¢ = {S AB, S a, A BS, A Abb, A ab, B SA, B BB, B a}.
Шаг 5. j = i – 1. Переход к шагу 2.
Шаг 2. (i = 2). Правила A BS, A Abb, A ab заменяем правилами: A BS, A ab, A BSA¢, A abA¢ и A¢ Bb, A¢ BbA¢. Получаем следующее множество правил: P¢ = { S AB, S a, A BS, A ab, A BSA¢, A abA¢, A¢ Bb, A¢ BbA¢, B SA, B BB, B a}.
Шаг 3. i = 3, j = 1.
Шаг 4. Используя правила S AB, S a, заменяем правило B à SA правилами B à ABA, B à aA. Получаем новое множество правил грамматики: P¢ = { S AB, S a, A BS, A ab, A BSA¢, A abA¢, A¢ Bb, A¢ BbA¢, B à ABA, B à aA}.
Шаг 5. j i – 1, j = 2. Переход к шагу 4.
Шаг 4. (i = 3, j = 2). Используя правила A BS, A ab, A BSA¢, A abA¢, заменяем правило B à ABA правилом B à aA, B à BSBA, B à abBA, B àBSA¢BA, B à abA¢BA и получаем новое множество правил грамматики P¢ = {S AB, S a, A BS, A ab, A BSA¢, A abA¢, A¢ Bb, A¢ BbA¢, B à aA, B à BSBA, B à abBA, B à BSA¢BA, B à abA¢BA}.
Шаг 5. j = i – 1. Переход к шагу 2.
Шаг 2. (i = 3). Правила B à BSBA, B à BSA¢BA, B à aA, B à abBA, B à abA¢BA заменяем правилами B à ab, B à abBA, B à abA¢BA, B à abB¢, B à abBAB¢, B à abA¢BAB¢, B¢à SBA, B¢à SA¢BA, B¢à SBAB¢, B¢à SA¢BAB¢.
Шаг 3. i = n, выход из алгоритма с окончательным множеством правил грамматики P¢ = {S AB, S a, A BS, A ab, A BSA¢, A abA¢, A¢ Bb, A¢ BbA¢, B à ab, B à abBA, B à abA¢BA, B à abB¢, B à abBAB¢, B à abA¢BAB¢, B¢à SBA, B¢à SA¢BA, B¢à SBAB¢, B¢à SA¢BAB¢}.
Исключение левой рекурсии
Формулировка задания
Исключить левую рекурсию из КС-грамматики G = <T, N, S, R>.
Задание.
2.2.4.6
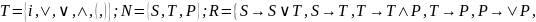
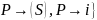
Решение:
I=1;
Заменим выражения стоящие слева от фигурной скобки на выражения, написанные справа от фигурной скобки
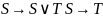



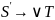

i=2
Повторим предыдущий шаг для i=2;

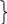
 T
T
 T
T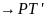
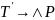
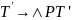
i=3;
Преобразования не требуются.
Новая грамматика, эквивалентная исходной:
 ,где
,где
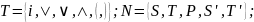
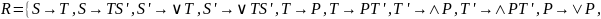
Исключение левой рекурсии
Исключить левую рекурсию из КС-грамматики G = < T, N, S, R >.
2.2.4.1. T = { a, b, с }, N = { S, A }, R = { S SaA, S AA, S b, A ASa, A Ab, A c };
i=1
S SaA; S AA, S b
после замены S AA, S b, S AAS’, S bS’, S’ aA, S’ aA S’
i=2, j=1
правил вида A2A1a нет.
j=i-1
j=1, i=2
A ASa, A Ab, A c
После замены A c, A cА’, A’ Sa, A’ b,
A’ SaA’, A’ bA’
R’={ S AA, S b, S AAS’, S bS’, S’ aA, S’ aA S’, A c, A cА’, A’ Sa, A’ b,
A’ SaA’, A’ bA },
N’={S,A,S’A’}
Грамматика без левой рекурсии -
G’={T,N’,S,R’}
Исключение левой рекурсии
Исключить левую рекурсию из КС-грамматики G = < T, N, S, R >.
2.2.4.1. T = { a, b, с }, N = { S, A }, R = { S ® SaA, S ® AA, S ® b, A ® ASa, A ® Ab, A ® c };
i=1
S ® SaA; S ® AA, S ® b
после замены S ® AA, S ® b, S ® AAS’, S ® bS’, S’ ® aA, S’ ® aA S’
i=2, j=1
правил вида A2®A1a нет.
j=i-1
j=1, i=2
A ® ASa, A ® Ab, A ® c
После замены A ® c, A ® cА’, A’ ® Sa, A’ ® b,
A’ ® SaA’, A’ ® bA’
R’={ S ® AA, S ® b, S ® AAS’, S ® bS’, S’ ® aA, S’ ® aA S’, A ® c, A ® cА’, A’ ® Sa, A’ ® b,
A’ ® SaA’, A’ ® bA },
N’={S,A,S’A’}
Грамматика без левой рекурсии -
G’={T,N’,S,R’}
Построение детерминированного конечного автомата по автоматной грамматике
Формулировка задания
Построить детерминированный конечный автомат по автоматной грамматике G = < T, N, S, R >. Определить язык, допускаемый конечным автоматом.
Задание.
3.2.1.3. 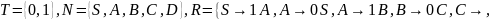

Решение:
Исключим - правила из грамматики.

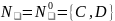
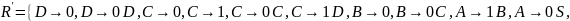

Запишем грамматику недетерминированного конечного автомата:
K
= ({S, A, B,
C, D, E},
{0, 1},
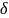 ,
S, {E}), где
функции переходов:
,
S, {E}), где
функции переходов:
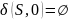


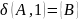
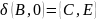
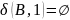

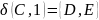
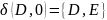
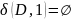
Преобразуем недетерминированный конечный автомат в детерминированный:
|
0 |
1 |
P0 {S} |
|
P1 {A} |
P1 {A} |
P0 {S} |
P2 {B} |
P2 {B} |
P3 {C, E} |
|
P3 {C, E} |
P3 {C, E} |
P4 {D, E} |
P4 {D, E} |
P4 {D, E} |
|
K’ = ({P0, P1, P2, P3, P4}, {1,0}, ’, P0, {P3, P4})
Граф переходов полученного детерминированного автомата

Функции переходов
(P0, 1) = P1
(P1, 0) = P0
(P1, 1) = P2
(P2, 0) = P3
(P3, 0) = P3
(P3, 1) = P4
(P4, 0) = P4
Описание языка, допускаемого конечным автоматом
Цепочки, принадлежащие языку – наборы 1 и 0, в начале которых стоит произвольное количество подцепочек “10” (≥0), далее стоит подцепочка “11”, далее стоит произвольное количество 0(>0), после чего цепочка либо заканчивается, либо стоит 1, после чего стоит произвольное количество 0.
(10)n11(0)m(1(0)k)p, где n≥0, m>0, k≥0, 0≤p≤1
Последовательность конфигураций конечного автомата при разборе цепочки, принадлежащей языку: 101011000100
(P0, 101011000100)
(P1, 01011000100)
(P0, 1011000100)
(P1, 011000100)
(P0, 11000100)
(P1, 1000100)
(P2, 000100)
(P3, 00100)
(P3, 0100)
(P3, 100)
(P4, 00)
(P4, 0)
(P4, )
)
Построение детерминированного конечного автомата по автоматной грамматике
Построить детерминированный конечный автомат (КА) по автоматной грамматике G = < T, N, S, R >. Определить язык, допускаемый конечным автоматом.
3.2.1.4. T = { 0, 1 }, N = { S, A, B }, R = { S , S 1S, S 0A, A 1S, A 0B, B , B 0B, B 1B };
Исключим e-правила
S->e
S->1S S->1
S->0A
A->1S A->1
A->0 A->0B
B->0 B->0B, B->1, B->1B
Функции переходов недетерминированного конечного автомата.
(S,1)={S,E}
(S,0)=A
(A,1)={S,E}
(A,0)={B,E}
(B,1)={B,E}
(B,0)={B,E}
Преобразование недетерминированного конечного автомата в детерминированный.
|
0 |
1 |
P0 {S} |
P1 {A} |
P2 {S,E} |
P1 {A} |
P3 {B,E} |
P2 {S,E} |
P2 {S,E} |
P1 {A} |
P2 {S,E} |
P3 {B,E} |
P3 {B,E} |
P3 {B,E} |
F={P0,P2,P3} q0=p0 {1,0} {P0,P1,P2,P3}
Г раф
переходов полученного детерминированного
автомата
раф
переходов полученного детерминированного
автомата
Функция переходов
(p0,0)=p1
(p0,1)=p2
(p1,0)=p3
(p1,1)=p2
(p2,0)=p1
(p2,1)=p2
(p3,0)=p3
(p3,1)=p3
Описание языка, допускаемого конечным автоматом.
Цепочки, принадлежащие языку – наборы 1 и 0, начало которых – последовательности 1 любой длины, резделяемые 0, конец – произвольная последовательность 1 и 0 любой длины. Начало и конец разделены двумя нулями
начало и/или конец могут отсутствовать
Последовательность конфигураций конечного автомата при разборе цепочки, принадлежащей языку 111101100100101001
(p0, 111101100100101001)
(p2, 11101100100101001)
(p2, 1101100100101001)
(p2, 101100100101001)
(p2, 01100100101001)
(p1,1100100101001)
(p2, 100100101001)
(p1, 00100101001)
(p3, 0100101001)
(p3, 100101001)
(p3, 00101001)
(p3, 0101001)
(p3, 101001)
(p3, 01001)
(p3, 1001)
(p3, 001)
(p3, 01)
(p3, 1)
(p3,ε)
p3 – одно из конечных состояний ДКА
Последовательность конфигураций конечного преобразователя при переводе цепочки, не принадлежащей языку. 11110
(p0, 11110)
(p2, 1110)
(p2, 110)
(p2, 10)
(p2, 0)
(p1, 11110)
Построение детерминированного конечного автомата по автоматной грамматике
Построить детерминированный конечный автомат (КА) по автоматной грамматике G = < T, N, S, R >. Определить язык, допускаемый конечным автоматом.
3.2.1.4. T = { 0, 1 }, N = { S, A, B }, R = { S ® e, S ® 1S, S ® 0A, A ® 1S, A ® 0B, B ® e, B ® 0B, B ®1B };
Исключим e-правила
S->e
S->1S S->1
S->0A
A->1S A->1
A->0 A->0B
B->0 B->0B, B->1, B->1B
Функции переходов недетерминированного конечного автомата.
d(S,1)={S,E}
d(S,0)=A
d(A,1)={S,E}
d(A,0)={B,E}
d(B,1)={B,E}
d(B,0)={B,E}
Преобразование недетерминированного конечного автомата в детерминированный.
d |
0 |
1 |
P0 {S} |
P1 {A} |
P2 {S,E} |
P1 {A} |
P3 {B,E} |
P2 {S,E} |
P2 {S,E} |
P1 {A} |
P2 {S,E} |
P3 {B,E} |
P3 {B,E} |
P3 {B,E} |
F={P0,P2,P3} q0=p0 {1,0} {P0,P1,P2,P3}
Г раф переходов полученного детерминированного автомата
Функция переходов
d(p0,0)=p1
d(p0,1)=p2
d(p1,0)=p3
d(p1,1)=p2
d(p2,0)=p1
d(p2,1)=p2
d(p3,0)=p3
d(p3,1)=p3
Описание языка, допускаемого конечным автоматом.
Цепочки, принадлежащие языку – наборы 1 и 0, начало которых – последовательности 1 любой длины, резделяемые 0, конец – произвольная последовательность 1 и 0 любой длины. Начало и конец разделены двумя нулями
начало и/или конец могут отсутствовать
Последовательность конфигураций конечного автомата при разборе цепочки, принадлежащей языку 111101100100101001
(p0, 111101100100101001)
(p2, 11101100100101001)
(p2, 1101100100101001)
(p2, 101100100101001)
(p2, 01100100101001)
(p1,1100100101001)
(p2, 100100101001)
(p1, 00100101001)
(p3, 0100101001)
(p3, 100101001)
(p3, 00101001)
(p3, 0101001)
(p3, 101001)
(p3, 01001)
(p3, 1001)
(p3, 001)
(p3, 01)
(p3, 1)
(p3,ε)
p3 – одно из конечных состояний ДКА
Последовательность конфигураций конечного преобразователя при переводе цепочки, не принадлежащей языку. 11110
(p0, 11110)
(p2, 1110)
(p2, 110)
(p2, 10)
(p2, 0)
(p1, 11110)
Построение детерминированного конечного преобразователя
Формулировка задания
Построить детерминированный конечный автомат по автоматной грамматике
Задание.
3.2.2.8. Определить детерминированный конечный преобразователь, преобразующий множество цепочек, в которых четное количество нулей ограничено произвольным числом единиц, во множество цепочек { 1n , где n – число групп с четным количеством нулей}. Цепочки разделяются запятой, последовательность цепочек заканчивается символом "#".
Решение:
Определим необходимые для заданного по условию преобразователя состояния:
q0 – начальное состояние;
q1–четное количество нулей;
q2–нечетное количество нулей;
q3–текущий символ 1 или , ;
q4–конечное состояние;
Опишем функции переходов:
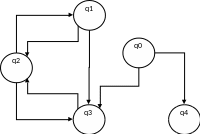 (q0,
#) = {(q4,
#)}
(q0,
#) = {(q4,
#)}
(q0, ,) = {(q3, ,)} 0
(q3, ,) = {(q3, ,)}
(q0, 1) = {(q3, ε)}
(q3, 1) = {(q3, ε)} 0 1 #
(q3, 0) = {(q2, ε)} ,
(q2, 0) = {(q1, ε)}
(q1, 0) = {(q2, ε)} 0 1
(q2, 1) = {(q3, ε)}
(q1, 1) = {(q3, 1)}
(q3, #) = {(q4, #)} 1 #
1 ,
Последовательность конфигураций и выходная цепочка конечного преобразователя при переводе цепочки, принадлежащей языку.
Входная цепочка: 110011,1101#
(q0, 110011,1101#, ε), (q3,10011,1101#,ε), (q3,0011,1101#,ε), (q2,011,1101#,ε), (q1,11,1101#,ε),
(q2,1,1101#, 1), (q3,,1101#, 1),(q3,1101#, 1,), (q3,101#, 1,),(q3,01#, 1,),(q2,1#, 1,),(q3,#, 1,),(q4,#, 1,).
Последовательность конфигураций и выходная цепочка конечного преобразователя при переводе цепочки, не принадлежащей языку.
Входная цепочка: 110011,1101
(q0, 110011,1101, ε), (q3,10011,1101,ε), (q3,0011,1101,ε), (q2,011,1101,ε), (q1,11,1101,ε),
(q2,1,1101, 1), (q3,,1101, 1), (q3,1101, 1,), (q3,101, 1,), (q3,01, 1,), (q2,1, 1,), (q3,ε, 1,).
Построение детерминированного конечного преобразователя
Определить конечный преобразователь, осуществляющий перевод последовательности составных имен (идентификаторов, разделенных символом ".") в последовательность цепочек 1n , где n – число простых идентификаторов, входящих в состав составного идентификатора. Элементы последовательности разделяются запятой, признаком конца последовательности является символ "#".
Функции переходов и выходов, таблица переходов и выходов и граф переходов и выходов детерминированного конечного преобразователя.
а – любой символ имени
(q0, a) = {(q1, )}
(q1, a) = {(q1, )}
(q1, .) = {(q2, 1)}
(q1, , ) = {(q3, 1)}
(q1, #) = {(qe, 1)}
(q2, a) = {(q1, )}
(q3, a) = {(q1, ,)}
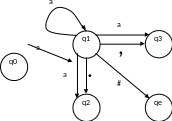
Последовательность конфигураций и выходная цепочка конечного преобразователя при переводе цепочки, принадлежащей языку.
AB.D,C,A# результат преобразования должен быть 11,1,1
(q0, AB.D,C,A#,) ->(q1, B.D,C,A#, )->(q1, .D,C,A#, )->(q2, D,C,A#,1)->(q1, ,C,A#, 1)->(q3, C,A#, 11)->(q1, ,A#, 11,)->(q3, A#, 11,1)->(q1, #, 11,1,)->(qe, , 11,1,1)
Последовательность конфигураций конечного преобразователя при переводе цепочки, не принадлежащей языку.
C.D,A.# данная цепочка не принадлежит языку.
(q0, C.D,A.#,) -> (q1, .D,A.#,) ->(q2, D,A.#, 1)-> (q1, ,A.#,1)-> (q3, A.#,11)-> (q1, .# ,11,)-> (q2, #, 11,1).
Построение детерминированного конечного преобразователя
Определить конечный преобразователь, осуществляющий перевод последовательности составных имен (идентификаторов, разделенных символом ".") в последовательность цепочек 1n , где n – число простых идентификаторов, входящих в состав составного идентификатора. Элементы последовательности разделяются запятой, признаком конца последовательности является символ "#".
Функции переходов и выходов, таблица переходов и выходов и граф переходов и выходов детерминированного конечного преобразователя.
а – любой символ имени
d(q0, a) = {(q1, e)}
d(q1, a) = {(q1, e)}
d(q1, .) = {(q2, 1)}
d(q1, , ) = {(q3, 1)}
d(q1, #) = {(qe, 1)}
d(q2, a) = {(q1, e)}
d(q3, a) = {(q1, ,)}
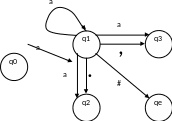
Последовательность конфигураций и выходная цепочка конечного преобразователя при переводе цепочки, принадлежащей языку.
AB.D,C,A# результат преобразования должен быть 11,1,1
(q0, AB.D,C,A#,e) ->(q1, B.D,C,A#, e)->(q1, .D,C,A#, e)->(q2, D,C,A#,1)->(q1, ,C,A#, 1)->(q3, C,A#, 11)->(q1, ,A#, 11,)->(q3, A#, 11,1)->(q1, #, 11,1,)->(qe, e, 11,1,1)
Последовательность конфигураций конечного преобразователя при переводе цепочки, не принадлежащей языку.
C.D,A.# данная цепочка не принадлежит языку.
(q0, C.D,A.#,e) -> (q1, .D,A.#,e) ->(q2, D,A.#, 1)-> (q1, ,A.#,1)-> (q3, A.#,11)-> (q1, .# ,11,)-> (q2, #, 11,1).
Построение детерминированного автомата (распознаватель) с магазинной памятью
Формулировка задания
Построить детерминированный автомат с магазинной памятью.
Задание
4.2.1.3. Построить детерминированный магазинный автомат, распознающий цепочки в алфавите { 0,1 } с одинаковым количеством нулей и единиц.
Решение
Функции переходов, для этого автомата будут выглядеть следующим образом:
(q0, 0, Z) = (q0, 0Z);
(q0, 1, Z) = (q0, 1Z);
(q0, 0, 0) = (q0, 00);
(q0, 1, 1) = (q0, 11);
(q0, 1, 0) = (q0, ε);
(q0, 0, 1) = (q0, ε);
(q0, ε, Z) = (q1, ε).
q1 – конечное состояние.
Последовательность конфигураций при разборе цепочки 110010, принадлежащей языку:
(q0, 110010, Z), (q0, 10010, 1Z), (q0, 0010, 11Z), (q0, 010, 1Z), (q0, 10, Z), (q0, 0, 1Z), (q0, ε, Z),(q1, ε, Z).
Последовательность конфигураций при разборе цепочки 1110, не принадлежащей языку:
(q0, 1110, Z), (q0, 110, 1Z), (q0, 10, 11Z), (q0, 0, 111Z), (q0, ε, 11Z). Из текущего состояния не возможно совершить переход.
Построение детерминированного автомата (распознаватель) с магазинной памятью Формулировка задания
Построить детерминированный магазинный автомат, распознающий цепочки из множества { 0n1n , n > 0 } { 1n0n , n > 0 }.
P= <{q0,q1,q2,q3,q4,q5,qe},{1,0},{1,0,Z}, ,Z, q0, qe>
Функции переходов:
(q0,1,Z)=(q1,1Z)
(q0,0,Z)=(q2,0Z)
(q1,1,1)=(q1,11)
(q1,0,1)=(q3,ε)
(q2,0,0)=(q2,00)
(q2,1,0)=(q4, ε)
(q3,0,1)=(q3,ε)
(q4,1,0)=(q4,ε)
(q3, ε ,Z)=(qe,ε)
(q4, ε,Z)=(qe,ε)
Последовательность конфигураций при разборе цепочки 111000, принадлежащей языку .
(q0, 111000, Z)├ (q1, 11000, 1Z) ├ (q1, 1000, 11Z) ├ (q1, 000, 111Z) ├ (q3, 00, 11Z) ├ (q3, 0, 1Z) ├ (q3, ε, Z) ├ (qe, ε, ε).
Последовательность конфигураций при разборе цепочки 00111, не принадлежащей языку .
(q0,00111,Z) ├ (q2,0111,0Z) ├ (q2,111,00Z) ├ (q4,11,0Z )├ (q4,1,Z)
Из данного состояния невозможно совершить переход.
Построение детерминированного автомата (распознаватель) с магазинной памятью
Формулировка задания
Построить детерминированный магазинный автомат, распознающий цепочки из множества { 0n1n , n > 0 } È { 1n0n , n > 0 }.
P= <{q0,q1,q2,q3,q4,q5,qe},{1,0},{1,0,Z},d ,Z, q0, qe>
Функции переходов:
d(q0,1,Z)=(q1,1Z)
d(q0,0,Z)=(q2,0Z)
d(q1,1,1)=(q1,11)
d(q1,0,1)=(q3,ε)
d(q2,0,0)=(q2,00)
d(q2,1,0)=(q4, ε)
d(q3,0,1)=(q3,ε)
d(q4,1,0)=(q4,ε)
d(q3, ε ,Z)=(qe,ε)
d(q4, ε,Z)=(qe,ε)
Последовательность конфигураций при разборе цепочки 111000, принадлежащей языку .
(q0, 111000, Z)├ (q1, 11000, 1Z) ├ (q1, 1000, 11Z) ├ (q1, 000, 111Z) ├ (q3, 00, 11Z) ├ (q3, 0, 1Z) ├ (q3, ε, Z) ├ (qe, ε, ε).
Последовательность конфигураций при разборе цепочки 00111, не принадлежащей языку .
(q0,00111,Z) ├ (q2,0111,0Z) ├ (q2,111,00Z) ├ (q4,11,0Z )├ (q4,1,Z)
Из данного состояния невозможно совершить переход.
Построение детерминированного преобразователя с магазинной памятью.
Формулировка задания
Построить детерминированный преобразователь с магазинной памятью.
Задание
4.2.2.4 Построить детерминированный преобразователь с магазинной памятью, осуществляющий перевод произвольной цепочки из множества { 0n1n 0m1m..., где n, m,...> 0 } в цепочку вида 1n+m+ .
Решение
Определим детерминированный преобразователь с магазинной памятью следующим образом:
P= <{q0,q1 },{1,0},{0, Z}, ,Z, q0, q1>
Функции переходов, для этого автомата будут выглядеть следующим образом:
(q0, 0 , Z) = (q0, 0Z, ε);
(q0, 0, 0) = (q0, 00, ε);
(q0, 1, 0) = (q0, ε, 1);
(q0, ε, Z) = (q1, ε, ε)
Преобразование цепочки 0001110011010011, принадлежащей языку:
(q0, 0001110011010011, Z), (q0, 001110011010011, 0Z), (q0, 01110011010011, 0Z),
(q0, 1110011010011, 000Z), (q0, 110011010011, 00Z), (q0, 10011010011, 0Z), (q0, 0011010011, Z),
(q0, 011010011, 0Z), (q0, 11010011, 00Z), (q0, 1010011, 0Z), (q0, 010011, Z), (q0, 10011, 0Z),
(q0, 0011, Z), (q0, 011, 0Z), (q0, 11, 00Z), (q0, 1, 0Z), (q1, ε, Z).
Преобразование цепочки 01001, не принадлежащей языку:
(q0, 01001, Z), (q0, 1001, 0Z), (q0, 001, Z), (q0, 01, 0Z), (q0, 1, 00Z), (q0, ε, 0Z). Из текущей конфигурации невозможно совершить переход.
Построение детерминированного преобразователя с магазинной памятью.
Формулировка задания
Построить детерминированный преобразователь с магазинной памятью, осуществляющий перевод произвольной цепочки из множества {13n+20n , n ≥ 0} в цепочку вида 1n0n.
P= <{q0,q1,q2,q4,q5, q6,q7 },{1,0},{1,0}{1,0,Z}, ,Z, q0, q7>
(q0,1,Z)=(q1,Z, ε)
(q1,1,Z)=(q2,Z, ε)
(q2,ε,Z)=(q7, ε, ε)
(q2,1,Z)=(q4,1Z, ε)
(q2,1,1)=(q4,11, ε)
(q2,0,1)=(q6, ε, 0)
(q4,1,Z)=(q5,Z, ε)
(q4,1,1)=(q5,1, ε)
(q5,1,Z)=(q2,1Z, 1)
(q5,1,1)=(q2,11, 1)
(q6, 0, 1)=(q6, ε, 0)
(q6, ε, Z)=(q7, ε, ε)
Преобразование цепочки 1111111100, принадлежащей языку.
(q0, 1111111100,Z, ε) ├ (q1, 111111100, Z, ε) ├ (q2, 11111100, Z, ε) ├ (q4, 1111100, Z, ε) ├ (q5, 111100, Z, ε) ├ (q2, 11100,1Z, 1) ├ (q4, 1100,1Z,1) ├ (q5, 100,1Z,1) ├ (q2, 00, 11Z, 11) ├ (q6, 0 ,1Z, 110) ├ (q6, ε, Z, 1100) ├ (q7, ε, ε, 1100)
Преобразование цепочки 1100, не принадлежащей языку.
(q0, 1100, Z, ε) ├ (q1, 100, Z, ε) ├ (q2, 00, Z, ε). Из текущей конфигурации невозможно совершить переход
Построение детерминированного преобразователя с магазинной памятью.
Формулировка задания
Построить детерминированный преобразователь с магазинной памятью, осуществляющий перевод произвольной цепочки из множества {13n+20n , n ≥ 0} в цепочку вида 1n0n.
P= <{q0,q1,q2,q4,q5, q6,q7 },{1,0},{1,0}{1,0,Z},d ,Z, q0, q7>
d(q0,1,Z)=(q1,Z, ε)
d(q1,1,Z)=(q2,Z, ε)
d(q2,ε,Z)=(q7, ε, ε)
d(q2,1,Z)=(q4,1Z, ε)
d(q2,1,1)=(q4,11, ε)
d(q2,0,1)=(q6, ε, 0)
d(q4,1,Z)=(q5,Z, ε)
d(q4,1,1)=(q5,1, ε)
d(q5,1,Z)=(q2,1Z, 1)
d(q5,1,1)=(q2,11, 1)
d(q6, 0, 1)=(q6, ε, 0)
d(q6, ε, Z)=(q7, ε, ε)
Преобразование цепочки 1111111100, принадлежащей языку.
(q0, 1111111100,Z, ε) ├ (q1, 111111100, Z, ε) ├ (q2, 11111100, Z, ε) ├ (q4, 1111100, Z, ε) ├ (q5, 111100, Z, ε) ├ (q2, 11100,1Z, 1) ├ (q4, 1100,1Z,1) ├ (q5, 100,1Z,1) ├ (q2, 00, 11Z, 11) ├ (q6, 0 ,1Z, 110) ├ (q6, ε, Z, 1100) ├ (q7, ε, ε, 1100)
Преобразование цепочки 1100, не принадлежащей языку.
(q0, 1100, Z, ε) ├ (q1, 100, Z, ε) ├ (q2, 00, Z, ε). Из текущей конфигурации невозможно совершить переход.
Построение недетерминированного МП-автомата по КС-грамматике
Формулировка задания
Построить недетерминированный МП-автомат по КС-грамматике.
Задание
4.2.3.11. T = { +, *, /, . }, N = { S, T, P, C }, R = { S S + T, S T, T T*P, T P, P .C., C /C, C / };
Решение
Определим функции перехода для МП-автомата:
(q, , S) = {(q, S+T), (q, T)}
(q, , T) = {(q, T*P), (q, P)}
(q, , P) = {(q, .C.)}
(q, , C) = {(q, /C), (q, /)}
(q, +, +) ={( q, )}
(q, *, *) ={( q, )}
(q, /, /) = {( q, )}
(q, ., .) = {( q, )}
Построение недетерминированного МП-автомата по КС-грамматике
T = { a, b, с }, N = { S, A }, R = { S SaA, S AA, S b, A ASa, A Ab, A c };
(q,,S)={(q,SaA),(q,AA),(q,b)}
(q,,A)={(q,Asa),(q, Ab),(q, c)}
(q,α, α)={(q, )} для α € { a, b, с }
Построение недетерминированного МП-автомата по КС-грамматике
T = { a, b, с }, N = { S, A }, R = { S ® SaA, S ® AA, S ® b, A ® ASa, A ® Ab, A ® c };
d(q,e,S)={(q,SaA),(q,AA),(q,b)}
d(q,e,A)={(q,Asa),(q, Ab),(q, c)}
d(q,α, α)={(q, e)} для α € { a, b, с }
Построение недетерминированного расширенного МП-автомата по КС-грамматике
Формулировка задания
Построить недетерминированный расширенный МП-автомат по КС-грамматике.
Задание
4.2.4.3. T = { a, b }, N = { S, A, B }, R = { S AB, S a, A BS, A Sb, B SA, B BB, B a };
Решение
P=({q, r}, {a, b}, {a, b, S, A, B, Z}, , q, Z, {r})
Определим функции перехода для расширенного МП-автомата:
(q, , AB) = {(q,S)}
(q, , a) = {(q, S), (q, B)}
(q, , BS) = {(q, A)}
(q, ,Sb) = {(q, A)}
(q, , SA) = {(q, B)}
(q, , BB) = {(q, B)}
(q, , ZS) = {(r, )}
(q, a, ) = {(q, a)}
(q, b,) = {(q, b)}
Пример 5.6
Определим расширенный МП-автомат с магазинной памятью, распознающий арифметические выражения из примера 5.3, следующим образом:
P = ({q, r}, {i, +, *, (, )}, {i, +, *, (, ), E, T, M}, , q, , {r}), в котором функция переходов определяется следующим образом:
(q, a, ) = {(q, a)} для всех a ,
(q, , E + T) = {(q, E)},
(q, , T) = {(q, E)},
(q, , T * M) = {(q, T)},
(q, , M) = {(q, T)},
(q, , i) = {(q, M)},
(q, , (E)) = {(q, M)},
(q, , E) = {(r, )}.
При анализе входной цепочки i + i * i МП-автомат P может выполнить следующую последовательность тактов:
(q, i + i * i, ) |
|
(q, + i * i, i) |
|
|
(q, + i * i, M) |
|
|
(q, + i * i, T) |
|
|
(q, + i * i, E) |
|
|
(q, i * i, E+) |
|
|
(q, * i, E+i) |
|
|
(q, * i, E+M) |
|
|
(q, * i, E+T) |
|
|
(q, i, E+T*) |
|
|
(q, , E+T*i) |
|
|
(q, , E+T*M) |
|
|
(q, , E+T) |
|
|
(q, , E) |
|
|
( q, , ). |
Построение недетерминированного расширенного мп-автомата по кс-грамматике
Построить недетерминированный расширенный МП-автомат по КС- грамматике
T = { a, b, с, d }, N = { S, A }, R = { S aA, S Ab, A Sc, A d };
P=({q, r}, {a, b, c, d}, {a, b, c, d, S, A,Z}, , q, Z, {r})
(q, t, )=(q, t), t €{ a, b, с, d }
(q, , аA)= (q, S)
(q, , Ab)= (q, S)
(q, , Sc)= (q, A)
(q, , d)= (q, A)
(q, , ZS)= (r, )
Построение недетерминированного расширенного мп-автомата по кс-грамматике
Построить недетерминированный расширенный МП-автомат по КС- грамматике
T = { a, b, с, d }, N = { S, A }, R = { S ® aA, S ® Ab, A ® Sc, A ® d };
P=({q, r}, {a, b, c, d}, {a, b, c, d, S, A,Z}, d, q, Z, {r})
d(q, t, e)=(q, t), t €{ a, b, с, d }
d(q, e, аA)= (q, S)
d(q, e, Ab)= (q, S)
d(q, e, Sc)= (q, A)
d(q, e, d)= (q, A)
d(q, e, ZS)= (r, e)
Построить управляющую таблицу и промоделировать работу LL(1)-анализатора для КС-грамматики G = < T, N, S, R >
Определение. Множество ПЕРВЫЙ (FIRST) — множество терминальных символов, которыми начинаются цепочки, выводимые из нетерминала A:
FIRST(A) = {a A l+ a, где ( )*}.
Определение. Множество СЛЕДУЮЩИЙ (FOLLOW) — множество терминальных символов, которые могут встретиться непосредственно справа от нетерминала A в некоторой сентенциальной форме:
FOLLOW(А) = {a S l* A и a FIRST ()}.
Пример 7.1
Для рассмотренной выше грамматики с правилами
-
(1)
S
aAS
(3)
A
cAS
(2)
S
b
(4)
A
множество FIRST(A) = {c}, а множество FOLLOW(A) = {a, b}, так как непосредственно справа от нетерминала A в сентенциальных формах может находиться символ S и FIRST(S) = {a, b}.
Определение. КС-грамматика G = (N, S, P, S) является LL(1)-грамматикой тогда и только тогда, когда для каждого A-правила грамматики
A 1 2 … n, n 1
выполняются следующие условия:
Множества FIRST(1), FIRST (2), …, FIRST (n) попарно не пересекаются.
Если i * , то FIRST (j) ∩ FOLLOW(A) = для 1 j n, i j.
Важным следствием этого определения является то, что леворекурсивная грамматика не может быть LL(1)-грамматикой.
Другое важное свойство LL(1)-грамматики – ее однозначност.
Алгоритм 7.1. Алгоритм построения управляющей таблицы М для LL(1)-грамматики.
Вход. LL(1)-грамматики G = (N, S, Р, S).
Выход. Корректная управляющая таблица M для грамматики G.
Описание алгоритма.
Таблица M определяется на множестве (N S {^}) ( {}) по следующим правилам:
Если A – правило вывода грамматики с номером i, то М(А, а) = (, i) для всех a , принадлежащих множеству FIRST().
Если FIRST(), то М(А, b) = (, i) для всех b FOLLOW(A).
М(a, a) = ВЫБРОС для всех a.
М(, ) = ДОПУСК.
В остальных случаях M(X, a) = ОШИБКА для X ( {}) и a {}.
Конец алгоритма
Рассмотрим, как строится управляющая таблица М для грамматики G1 с правилами:
(1) |
E |
|
TE |
|
(5) |
T |
|
*PT¢ |
(2) |
E |
|
+TE |
|
(6) |
T |
|
e |
(3) |
E |
|
|
|
(7) |
P |
|
i |
(4) |
T |
|
PT¢ |
|
(8) |
P |
|
(E) |
Управляющая таблица должна содержать 11 строк, помеченных символами из множества (N È S È {^}), и 6 столбцов, помеченных символами из множества (S È {e}).
Заполнение таблицы начнем с выполнения шага 1 алгоритма.
Шаг 1. Будем строить таблицу построчно, для чего последовательно рассматриваем все нетерминальные символы.
Нетерминал E.
Этому символу соответствует правило вывода грамматики
E TE. Так как FIRST(TE) = { (, i}, то следовательно,
M(E, ( ) = M(E, i) = ( TE, 1).
Для нетерминала E в грамматике имеется два правила вывода: (2) и (3).
Для правила (2) E + TE множество FIRST(+TE) = {+} и, следовательно, M(E, +) = (+TE, 2).
Правило (3) имеет пустую правую часть, поэтому необходимо вычислить множество символов, следующих за нетерминалом E¢ в сетенциальных формах. Построив левый вывод E TE¢ PT¢E¢ (E)T¢E¢ (TE¢)TE¢…, получим FOLLOW(E) = { ), e).
Таким образом, M(E¢, ) ) = M(E¢, ) = (, 3).
Выполняя шаг 1 алгоритма для нетерминалов Т, T¢’ и Р, получим:
-
Правило грамматики
Множество
Значение M
(4)
T
PT¢
FIRST(PT¢)
=
{ (, i)}
M(T¢, ( ) = M(T¢, i) = (PT¢, 4)
(5)
T
*PT¢
FIRST(*PT¢)
=
{*}
M(T¢, *) = (*PT¢, 5)
(6)
T
e
FOLLOW(T¢)
=
{+, ), e}
M(T¢,+) = M(T¢, )) = M(T¢,e) = (e,6)
(7)
P
i
FIRST(i)
=
{i}
M(P, i ) = (i, 7)
(8)
P
(E)
FIRST((E))
=
{(}
M(P, ( ) = ((E), 8)
Шаг 2. Далее всем элементам таблицы, находящимся на пересечении строки и столбца, отмеченным одним и тем же терминальным символом, присвоим значение ВЫБРОС.
Шаг 3. Элементу таблицы М(, ) припишем значение ДОПУСК.
Шаг 4. Остальным элементам таблицы присвоим значение ОШИБКА.
В заключение, можно сравнить таблицу, построенную при помощи алгоритма 7.1, с управляющей таблицей, приведенной на рис. 7.5 и убедиться, что они совпадают. В [3] доказано, что алгоритм 7.1 строит корректную управляющую таблицу.
Формулировка задания
Построить управляющую таблицу и промоделировать работу LL(1)-анализатора для КС-грамматики G = < T, N, S, R >.
Задание
5.2.3.
 ^
^ ^
^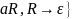
Решение
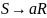 ,
,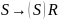 ,
,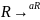 ,
, .
.
Определим множества FIRST и FOLLOW для всех нетерминальных символов
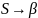
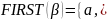
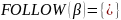
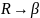
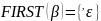
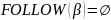
Построим управляющую таблицу для грамматики G.
|
a |
( |
) |
^ |
ε |
S |
aR,1 |
(S)R, 2 |
ОШИБКА |
ОШИБКА |
ОШИБКА |
R |
ОШИБКА |
ОШИБКА |
ОШИБКА |
^aR, 3 |
ε, 4 |
a |
ВЫБРОС |
ОШИБКА |
ОШИБКА |
ОШИБКА |
ОШИБКА |
( |
ОШИБКА |
ВЫБРОС |
ОШИБКА |
ОШИБКА |
ОШИБКА |
) |
ОШИБКА |
ОШИБКА |
ВЫБРОС |
ОШИБКА |
ОШИБКА |
^ |
ОШИБКА |
ОШИБКА |
ОШИБКА |
ВЫБРОС |
ОШИБКА |
┴ |
ОШИБКА |
ОШИБКА |
ОШИБКА |
ОШИБКА |
ДОПУСК |
Контрольный пример – разбор цепочки “(a^a)^a”, порождаемой этим алгоритмом.
((a^a)^a, S┴
,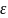 )
->
M((S)R,2)
)
->
M((S)R,2)
((a^a)^a,(S)R┴ ,2) ->ВЫБРОС
(а^а)^а, S)R┴ ,2) -> M(aR,1)
(a^a)^a, aR)R┴ , 21) ->ВЫБРОС
(^a)^a, R)R┴ , 21) -> M(^aR, 3)
(^a)^a, ^aR)R┴ , 213) ->ВЫБРОС
(a)^a, aR)R┴ , 213) ->ВЫБРОС
()^a, R)R┴ , 213) -> M( ,4)
()^a, )R┴ , 2134) ->ВЫБРОС
(^a, R┴ , 2134) -> M(^aR, 3)
(^a, ^aR┴ , 21343) ->ВЫБРОС
(a, aR┴ , 21343) ->ВЫБРОС
( , R┴, 21343) ->M( ,4)
( ,┴ , 213434) ->ДОПУСК
Построить управляющую таблицу и промоделировать работу LL(1)-анализатора для КС-грамматики G = < T, N, S, R >
T = { a, b, c, d, e }, N = { S, A, B }, R = { S ® aAB, S ® bBS, S ® e, A ® cBS, A ® e, B ® dB, B ® e };
1. S ® aAB,
2. S ® bBS,
3. S ® e,
4.A ® cBS,
5.A ® e,
6.B ® dB,
7.B ® e
S® β
FIRST(β)={a,b,e}
A® β
FIRST(β)={c, e}
B® β
FIRST(β) = {d, e}
|
A |
b |
c |
d |
e |
S |
aAB,1 |
bBS,2 |
|
e,3 |
e,3 |
A |
|
|
сBS,4 |
e,5 |
e,5 |
B |
e,7 |
e,7 |
|
dB,6 |
e,7 |
a |
B |
|
|
|
|
b |
|
B |
|
|
|
c |
|
|
B |
|
|
d |
|
|
|
B |
|
┴ |
|
|
|
|
Д |
Контрольный пример – разбор цепочки, порождаемой этим алгоритмом
acdbd
(acdbd,S┴, e)->
(acdbd,aAB┴,1)->
(cdbd,AB┴,1)->
(cdbd,cBSB┴,14)->
(dbd,BSB┴,14)->
(dbd,dBSB┴,146)->
(bd,BSB┴,146)->
(bd,SB┴,1467)->
(bd,bBSB┴,14672)->
(d,BSB┴,14672)->
(d,dBSB┴,146726)->
(e,BSB┴,146726)->
(e,SB┴,1467267)->
(e,B┴,14672673)->
(e,┴,146726737)
M(S,a)=(aAB,1)
ВЫБРОС
M(A,c)=(cBS,4)
ВЫБРОС
M(B,d)=(dB,6)
ВЫБРОС
M(B,b)=(e,7)
M(S,b)=(bBS,2)
ВЫБРОС
M(B,d)=(dB,6)
ВЫБРОС
M(B, e)=(e,7)
M(S, e)=(e,3)
M(B, e)=(e,7)
ДОПУСК
Построить управляющую таблицу и промоделировать работу LL(1)-анализатора для КС-грамматики G = < T, N, S, R >
Формулировка задания:
Построить управляющую таблицу и промоделировать работу LL(1)-анализатора для КС-грамматики G = < T, N, S, R >.
T = { a, b, c, d, e }, N = { S, A, B }, R = { S aAB, S bBS, S , A cBS, A , B dB, B };
1. S aAB,
2. S bBS,
3. S ,
4.A cBS,
5.A ,
6.B dB,
7.B
S β
FIRST(β)={a,b,}
A β
FIRST(β)={c, }
B β
FIRST(β) = {d, }
|
A |
b |
c |
d |
e |
S |
aAB,1 |
bBS,2 |
|
,3 |
,3 |
A |
|
|
сBS,4 |
,5 |
,5 |
B |
,7 |
,7 |
|
dB,6 |
,7 |
a |
B |
|
|
|
|
b |
|
B |
|
|
|
c |
|
|
B |
|
|
d |
|
|
|
B |
|
┴ |
|
|
|
|
Д |
Контрольный пример – разбор цепочки, порождаемой этим алгоритмом
acdbd
(acdbd,S┴, )->
(acdbd,aAB┴,1)->
(cdbd,AB┴,1)->
(cdbd,cBSB┴,14)->
(dbd,BSB┴,14)->
(dbd,dBSB┴,146)->
(bd,BSB┴,146)->
(bd,SB┴,1467)->
(bd,bBSB┴,14672)->
(d,BSB┴,14672)->
(d,dBSB┴,146726)->
(,BSB┴,146726)->
(,SB┴,1467267)->
(,B┴,14672673)->
(,┴,146726737)
M(S,a)=(aAB,1)
ВЫБРОС
M(A,c)=(cBS,4)
ВЫБРОС
M(B,d)=(dB,6)
ВЫБРОС
M(B,b)=(,7)
M(S,b)=(bBS,2)
ВЫБРОС
M(B,d)=(dB,6)
ВЫБРОС
M(B, )=(,7)
M(S, )=(,3)
M(B, )=(,7)
ДОПУСК
Построить управляющую таблицу и промоделировать работу LR(0)- анализатора для КС-грамматики G = < T, N, S, R >.
Пусть Хi и Zi – грамматические вхождения символов Х и Z в правую часть i-го правила, a Yj – грамматическое вхождение символа Y в правую часть j-го правила. Определим множество OFIRST (Yi) (входит первым), в которое включим Yj и все грамматические вхождения, которыми могут начинаться цепочки, выводимые из Y.
OFIRST(Yi) = {Yj } {Xi Y A X и Xi – самое левое грамматическое вхождение в правую часть правила A X}.
Замечание
Если в грамматике есть правила с пустой правой частью, то на последнем шаге вывода они не применяются.
Используя множества OFIRST, определим отношение OBLOW (входит под) следующим образом:
Xi OBLOW Yj – это множество {(Xi, Yj) A XiZi P и Yj OFIRST (Zi) }.
OBLOW Yj – это множество {(,Yj) Yj OFIRST (S0) }, где S0 – начальное вхождение.
Отношение Xi OBLOW Yj определяет множество Q грамматических вхождений Xi, для которых представляющие их магазинные символы могут встретиться в магазине непосредственно под символом, представляющим Yj.
Отношение OBLOW будем задавать с помощью матрицы, содержащей n столбцов и n+1 строк, где n – число грамматических вхождений пополненной грамматики G. Первые n строк и столбцы матрицы отмечены грамматическими вхождениями, а последняя строка – маркером дна магазина. Если Xi OBLOW Yj, то элемент матрицы, расположенный в строке Xi и столбце Yj, равен 1.
Построим матрицу отношения OBLOW для грамматики с правилами:
(1) |
S |
à |
aAb |
|
(4) |
A |
à |
Bb |
(2) |
S |
à |
c |
|
(5) |
B |
à |
aA |
(3) |
A |
à |
bS |
|
(6) |
B |
à |
c |
Непосредственно из правил вывода грамматики (1) и (4) получим:
A1 OBLOW b1 и B4 OBLOW b4.
Из определения отношения OBLOW следует, что OBLOW Yj тогда и только тогда, когда Yj OFIRST(S0). Из S можно вывести цепочки S a1A1b1 и S c2. Следовательно, OFIRST(S0) = {a1, c2, S0} и OBLOW а1, OBLOW c2 и OBLOW S0.
Рассмотрим правило грамматики с номером (1). Из определения отношения OBLOW следует, что
a1 OBLOW Yj для всех Yj OFIRST(A1).
Из А можно вывести цепочки:
A b3S3, A B4b4 c6b4, A B4b4 a5A5b4.
Следовательно, OFIRST(А1) = {a5, b3, c6, A1, B4} и a1 OBLOW a5, a1 OBLOW b3, a1 OBLOW c6, a1 OBLOW A1, a1 OBLOW B4.
Поступая подобным образом для правил (3) и (6), получим матрицу отношения OBLOW:
|
S0 |
a1 |
A1 |
b1 |
c2 |
b3 |
S3 |
B4 |
b4 |
a5 |
A5 |
c6 |
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
1 |
|
|
1 |
|
1 |
|
1 |
|
1 |
A1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
b3 |
|
1 |
|
|
1 |
|
1 |
|
|
|
|
|
S3 |
|
|
|
|
|
|
|
|
|
|
|
|
B4 |
|
|
|
|
|
|
|
|
1 |
|
|
|
b4 |
|
|
|
|
|
|
|
|
|
|
|
|
a5 |
|
|
|
|
|
1 |
|
1 |
|
1 |
1 |
1 |
A5 |
|
|
|
|
|
|
|
|
|
|
|
|
c6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
Опишем алгоритм построения управляющей таблицы T LR(0)-анализатора (множества LR(0)-таблиц) для LR(0)-грамматики, не содержащей правил с пустой правой частью. Этот алгоритм можно также использовать для проверки принадлежности КС-грамматики классу LR(0).
Алгоритм 8.2. Построение множества LR(0)-таблиц.
Вход. LR(0)-грамматика G = (N, S, Р, S), не содержащая -правил.
Выход. Множество T LR(0)-таблиц для грамматики G или сообщение о том, что грамматика G не является LR(0)-грамматикой.
Описание алгоритма.
Построить пополненную грамматику G для исходной грамматики G.
Вычислить отношения OBLOW для грамматических вхождений грамматики G.
Определить функции переходов g(Х) следующим образом:
Построить таблицу, содержащую по одному столбцу для каждого символа из {} и одной отроке для каждого грамматического вхождения грамматики G¢ и маркера дна. Элемент в строке, помеченной грамматическим вхождением Хi или маркером дна , и столбце, отмеченном символом грамматики Y, должен содержать все грамматические вхождения, для которых справедливо отношение Хi OBLOW Yj. Заметам, что некоторые элементы построенной таким образом таблицы могут содержать более одного грамматического вхождения, т.е. таблица может быть недетерминированной.
Интерпретируя построенную таблицу как таблицу конечного автомата (состояния - грамматические вхождения и маркер дна (начальное состояние), а входные символы - символы из {}), определить тип автомата: детерминированный или недетерминированный. Недетерминированный автомат преобразовать в эквивалентный ему детерминированный автомат.
Определить магазинный алфавит Vp так, чтобы каждому состоянию детерминированного конечного автомата соответствовал ровно один магазинный символ.
В качестве символов алфавита Vp можно использовать любые символы, не являющиеся символами грамматики G¢ Для сохранения наглядности цепочек, представимых магазином, будем считать, что символы из Vp совпадают по написанию с соответствующими грамматическими вхождениями. Если магазинный символ представляет множество грамматических вхождений, то индексы магазинных символов будем обозначать строчными латинскими буквами.
Заменить совокупности грамматических вхождений, отмечающих состояния автомата, соответствующими символами из Vp.
Полученная таблица представляет собой таблицу функций переходов g(X) LR(0)-анализатора, причем элементы таблицы, соответствующие переходу в пустое множество состояний, имеют значение ОШИБКА.
4. Определить функции действия f(a) для всех магазинных символов, каждому из которых соответствует одна строка таблицы. Количество столбцов таблицы f(a) определяется количеством символов множества S È{e}. Элементы таблицы f(a) определяются следующим образом.
Если магазинному символу Т соответствует единственное вхождение S0, то в строке, отмеченной символом Т, f() = ДОПУСК, а все остальные элементы – ОШИБКА.
Если магазинному символу Т соответствует только одно грамматическое вхождение Xi, являющееся самым правым вхождением в i-е правило вывода грамматики G, то все элемента строки, помеченной Т, имеют значение (СВЕРТКА, i).
Если магазинному символу Т соответствует маркер дна магазина или все грамматические вхождения, представляемые символом Т, не являются самыми правыми в своих правилах, то в строке, отмеченной Т, f() = ошибка, а значения остальных элементов – ПЕРЕНОС.
Если множество вхождений, соответствующее магазинному символу Т, содержит начальное вхождение S0 и хотя бы еще одно вхождение, отличное от S0, которое не является самым правым в своем правиле, то в строке, отмеченной Т, f() = ДОПУСК, а значение всех остальных элементов – ПЕРЕНОС.
Если имеется множество грамматических вхождений, не удовлетворяющих перечисленным выше условиям, то G не является LR(0)-грамматикой.
Если построение f(a) закончено успешно, то грамматика является LR(0)-грамматикой, а таблица, полученная объединением таблиц, задающих функции f(a) и g(X) – управляющей таблицей T LR(0)-анализатора.
Конец алгоритма
Построим управляющую таблицу LR(0)-анализатора для грамматики, имеющей следующие правила:
(1) |
E |
à |
E + T |
|
(3) |
T |
à |
(E) |
(2) |
E |
à |
T |
|
(4) |
T |
à |
i |
Шаг 1. Определим пополненную грамматику для грамматики G:
G= (N {S}, S, Р {S E}, S).
Шаг 2. Вычислим отношение OBLOW для грамматических вхождений грамматики G¢. Матрица отношения OBLOW имеет вид:
-
E0
E1
+1
T1
T2
(3
E3
)3
i4
E0
E1
1
+1
1
1
1
T1
T2
(3
1
1
1
1
1
E3
1
)3
i4
1
1
1
1
1
Шаг 3. Определим функции переходов g(X).
Используя отношение OBLOW, построим таблицу переходов конечного (в данном случае недетерминированного) автомата:
E
T
(
)
i
+
E0
E1
+1
+1
T1
(3
i4
T1
T2
(3
E1, E3
T2
(3
i4
E3
)3
)3
i4
E0, E1
T2
(3
i4
Преобразуем недетерминированный автомат в эквивалентный ему детерминированный автомат, таблица переходов которого будет иметь вид:
E
T
(
)
i
+
{}
(E0, E1}
{T2}
{(3}
{i4}
{E0, E1}
{+1}
{T2}
{(3}
{ E1, E3}
{T2}
{(3}
{i4}
{i4}
{+1}
{T1}
{(3}
{i4}
{E1, E3}
{)3}
{+1}
{T1}
{)3}
Определим множество магазинных символов:
{E0, E1 }
{E1, E3 }
{}
{T2}
{(3}
{i4}
{+1}
{T1}
{)3}
Vp
Ex
Ey
T2
(3
i4
+1
T1
)3
Тогда функции переходов g(Х) LR(0)-анализатора для грамматики G имеет вид:
-
g(X)
E
T
(
)
i
+
Ex
T2
(3
i4
Ex
+1
T2
(3
Ey
T2
(3
i4
i4
+1
T1
(3
i4
Ey
)3
+1
T1
)3
Шаг 4. Определим функции действия f(a). Построим таблицу, содержащую по одной строке для каждого магазинного символа и одному столбцу для каждого символа a ( {}).
Для строки таблицы, отмеченной символом , соответствующее множество грамматических вхождений состоит из единственного символа , поэтому в этой отроке f() = ОШИБКА, а значения остальных элементов – ПЕРЕНОС.
Множество грамматических вхождений, соответствующих магазинному символу Еx, содержит два элемента: Е0 и Е1. Так как в это множество входит начальное вхождение E0, а вхождение Е1 не является самым правым в правиле грамматики (1), то f() = ДОПУСК, а остальные элементы строки, отмеченные символом Еx, имеют значение ПЕРЕНОС.
Магазинному символу Т2 соответствует единственное грамматическое вхождение Т2, которое является самым правым в правиле вывода (2) грамматики. Следовательно, значение всех элементов строки, помеченной Т2, – (СВЕРТКА, 2).
Поступая подобным образом для остальных строк, получим таблицу функций переходов f(a):
-
f(a)
(
)
i
+
П
П
П
П
Ex
П
П
П
П
Д
T2
С,2
С,2
С,2
С,2
С,2
(3
П
П
П
П
i4
С,4
С,4
С,4
С,4
С,4
+1
П
П
П
П
Ey
П
П
П
П
T1
С,1
С,1
С,1
С,1
С,1
)3
С,3
С,3
С,3
С,3
С,3
Поскольку при построении функции переходов f(a) не возникло конфликтных ситуаций, рассмотренная грамматика является LR(0)-грамматикой. Объединив функции g(X) и f(a) в одну таблицу, получим для управляющую таблицу T LR(0)-анализатора.
Формулировка задания
Построить управляющую таблицу и промоделировать работу LR(0)- анализатора для КС-грамматики G = <T, N, S, R>.
Задание
6.1.3. T { a, (, ), , }, N = { S, R}, R = { S a, S (SR, R ,SR, R )};
Построение управляющей таблицы
Дополним исходную грамматику правилом S’ S, тем самым получим пополненную грамматику G’ = <T, N’, S’, R’ >:
T { a, (, ), , }, N’ = { S’, S, R}, R = { S’S, S a, S (SR, R ,SR, R )};
Пронумеруем правила:
S’S
S a
S (SR
R ,SR
R )
Рассмотрим правило с №2: (2OBLOWYjдля всех Yjϵ OFIRST(S2).
Из Sможно вывести цепочки Sa; S (SR.
Следовательно, OFIRST(S2) = { a1, (2, S2} и(2OBLOW a1, (2OBLOW (2, (2OBLOW S2.
Поступая подобным образом для правила 3, получим матрицу отношения OBLOW.
|
S0 |
a1 |
(2 |
S2 |
R2 |
,3 |
S3 |
R3 |
)4 |
S0 |
|
|
|
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
(2 |
|
+ |
+ |
+ |
|
|
|
|
|
S2 |
|
|
|
|
+ |
+ |
|
|
+ |
R2 |
|
|
|
|
|
|
|
|
|
,3 |
|
+ |
+ |
|
|
|
+ |
|
|
S3 |
|
|
|
|
|
+ |
|
+ |
+ |
R3 |
|
|
|
|
|
|
|
|
|
)4 |
|
|
|
|
|
|
|
|
|
┴ |
+ |
+ |
+ |
|
|
|
|
|
|
Определим функцию переходов g(X): используя отношение OBLOW, построим таблицу переходов конечного автомата.
g(X) |
S |
R |
a |
( |
) |
, |
S0 |
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
(2 |
S2 |
|
a1 |
(2 |
|
|
S2 |
|
R2 |
|
|
)4 |
,3 |
R2 |
|
|
|
|
|
|
,3 |
S3 |
|
a1 |
(2 |
|
|
S3 |
|
R3 |
|
|
)4 |
,3 |
R3 |
|
|
|
|
|
|
)4 |
|
|
|
|
|
|
┴ |
S0 |
|
a1 |
(2 |
|
|
Получившаяся таблица переходов соответствует детерминированному автомату, тогда множеству магазинных символов соответствует первый столбец таблицы.
Определим функции действия f(a). Построим таблицу, содержащую по одной строке для каждого магазинного символа и по одному столбцу для каждого символа aϵ (T˅ {ε})
f(a) |
a |
( |
) |
, |
ε |
S0 |
|
|
|
|
Д |
a1 |
С,1 |
С,1 |
С,1 |
С,1 |
С,1 |
(2 |
П |
П |
П |
П |
|
S2 |
П |
П |
П |
П |
|
R2 |
С,2 |
С,2 |
С,2 |
С,2 |
С,2 |
,3 |
П |
П |
П |
П |
|
S3 |
П |
П |
П |
П |
|
R3 |
С,3 |
С,3 |
С,3 |
С,3 |
С,3 |
)4 |
С,4 |
С,4 |
С,4 |
С,4 |
С,4 |
┴ |
П |
П |
П |
П |
|
Контрольный пример –разбор цепочки «(а, а, а)» принадлежащей языку.
(┴, (a,a,a) ,ε)
(┴(2 , a,a,a),ε)
(┴(2a1, ,a,a), ε)
(┴(2S2, ,a,a), 1)
(┴(2S2,3 , a,a), 1)
(┴(2S2,3a1, , a), 1)
(┴(2S2,3S3, ,a), 11)
(┴(2S2,3S3,3 ,a), 11)
(┴(2S2,3S3,3a1, ), 11)
(┴(2S2,3S3,3S3, ), 111)
(┴(2S2,3S3,3S3), ε, 111)
(┴(2S2,3S3,3S3R3, ε, 1114)
(┴(2S2,3S3R3, ε, 11143)
(┴(2S2R2, ε, 111433)
(┴S0, ε, 1114332)
ДОПУСК.
Построить управляющую таблицу и промоделировать работу SLR(1)-анализатора для КС-грамматики G = < T, N, S, R >
Усовершенствуем алгоритм 8.2 построения управляющей таблицы так, чтобы получить анализатор для некоторого класса грамматик, не принадлежащих классу LR(0)-грамматик. Этот класс грамматик является подклассом LR(1)-грамматик и получил название SLR(1)-грамматик без -правил. Буква S в названии грамматики является сокращением английского слова Simple (простой).
Начнем с рассмотрения примера.
Построим управляющую таблицу LR(0)-анализатора для грамматики G0, правила вывода которой после пополнения имеют вид:
(0) |
E¢ |
à |
E |
|
|
|
|
|
(1) |
E |
à |
E + T |
|
(4) |
T |
à |
P |
(2) |
E |
à |
T |
|
(5) |
P |
à |
(E) |
(3) |
T |
à |
T*P |
|
(6) |
P |
à |
i |
В процессе построения анализатора получаем:
матрицу отношения OBLOW, определенную на множестве грамматических вхождений пополненной грамматики:
-
E0
E1
+1
T1
T2
T3
3
P3
P4
(5
E5
)5
i6
E0
E1
1
+1
1
1
1
1
1
T1
T2
T3
1
3
1
1
1
P3
P4
(5
E5
1
1
1
1
1
1
1
)5
1
i6
1
1
1
1
1
1
1
таблицу переходов недетерминированного конечного автомата:
-
+
(
)
i
E
T
P
(5
i6
E0, E1
T2, T3
P4
E0
E1
+1
+1
(5
i6
T1, T3
P4
T1
T2
T3
3
3
(5
i6
P3
P3
P4
(5
(5
i6
E1, E5
T2, T3
P4
E5
)5
)5
i6
таблицу переходов детерминированного конечного автомата:
+
(
)
i
E
T
P
{}
{(5}
{i6}
{E0, E1}
{T2, T3}
{P4}
{(5}
{(5}
{i6}
{E1, E5}
{T2, T3}
{P4}
{i6}
{E0, E1}
{+1}
{T2, T3}
{*3}
{P4}
{E1, E5}
{+1}
{)5}
{+1}
{(5}
{i6}
{T1, T3}
{P4}
{3}
{(5}
{i6}
{P3}
{)5}
{T1, T3}
{3}
{P3}
таблицу кодирования магазинных символов:
-
{Eo,E1}
{E1,E5}
{T2,T3}
{T1,T3}
{P3}
{P4}
{+1}
{3}
{(5}
{)5}
{i6}
{}
Vp
Ex
Ey
Tx
Ty
P3
P4
+1
3
(5
)5
i6
таблицу функций переходов g(X):
-
g(X)
+
(
)
i
E
T
P
(5
i6
Ex
Tx
P4
(5
(5
i6
Ey
Tx
P4
i6
Ex
+1
Tx
3
P4
Ey
+1
)5
+1
(5
i6
Ty
P4
3
(5
i6
P3
)5
Ty
3
P3
Выполняя шаг 4 алгоритма, обнаруживаем, что Go не принадлежит классу LR(0)-грамматик, так как множества грамматических вхождений, соответствующие магазинным символам Тx и Ty, содержат самые правые вхождения символа Т и не являются одноэлементными.
Покажем, как, сделав некоторый дополнительный анализ, можно определить функции действия f(a) для данной грамматики. Анализ выполняется для каждого элемента отроки таблицы отдельно и использует текущий входной символ (k = 1).
Рассмотрим, например, элемент управляющей таблицы для магазинного символа Тx, которому соответствует множество грамматических вхождений {Т2, Т3}. Наличие в Тx самого правого вхождения Т2 в правило вывода (2) говорит о том, что необходимо выполнить операцию (СВЕРТКА, 2), а тот факт, что в Тx содержится T3, свидетельствует в пользу операции ПЕРЕНОС.
Допустим, что входным символом является символ «+». Для магазинного символа Тx функция g(+) = ОШИБКА, поэтому втолкнуть его в магазин невозможно, и, следовательно, для допустимых входных цепочек в строке Тx функции действий должно быть значение f(+) = (СВЕРТКА, 2).
Для входного символа «» функция переходов g() = 3, значит, при анализе допустимых входных цепочек перенос в магазин символа «» будет правильным действием. Выполнение операции (СВЕРТКА, 2) в этом случае привело бы к тому, что в магазин был бы помещен магазинный символ, представляющий нетерминал Е. Так как входным символом при этом остается «», то на следующем шаге был бы выработан сигнал об ошибке, поскольку символ «» не может непосредственно следовать за Е («» не принадлежит множеству Follow(Е)). Таким образом, операция (СВЕРТКА, 2) исключается, и в строке управляющей таблицы, помеченной Тx , f() = ПЕРЕНОС.
Принципы, продемонстрированные при выполнении данного примера, позволяют на основе алгоритма 8.2 сформулировать алгоритм построения управляющей таблицы для SLR(1)-грамматик.
Алгоритм 8.3. Построение множества SLR(1)-таблиц.
Вход. SLR(1)-грамматика G = (N, S, Р, S), не содержащая -правил.
Выход. Множество T SLR(1)-таблиц для грамматики G или сообщение о том, что грамматика G не является SLR(1)-грамматикой.
Описание алгоритма.
Построить пополненную грамматику G для исходной грамматики G.
Вычислить отношения OBLOW для грамматических вхождений грамматики G.
Определить функции переходов g(Х) следующим образом:
Построить таблицу, содержащую по одному столбцу для каждого символа из {} и одной отроке для каждого грамматического вхождения грамматики G¢ и маркера дна. Элемент в строке, помеченной грамматическим вхождением Хi или маркером дна , и столбце, отмеченном символом грамматики Y, должен содержать все грамматические вхождения, для которых справедливо отношение Хi OBLOW Yj. Заметам, что некоторые элементы построенной таким образом таблицы могут содержать более одного грамматического вхождения, т.е. таблица может быть недетерминированной.
Интерпретируя построенную таблицу как таблицу конечного автомата (состояния — грамматические вхождения и маркер дна (начальное состояние), а входные символы — символы из {}), определить тип автомата: детерминированный или недетерминированный. Недетерминированный автомат преобразовать в эквивалентный ему детерминированный автомат.
Определить магазинный алфавит Vp так, чтобы каждому состоянию детерминированного конечного автомата соответствовал ровно один магазинный символ.
В качестве символов алфавита Vp можно использовать любые символы, не являющиеся символами грамматики G¢. Для сохранения наглядности цепочек, представимых магазином, будем считать, что символы из Vp совпадают по написанию с соответствующими грамматическими вхождениями. Если магазинный символ представляет множество грамматических вхождений, то индексы магазинных символов будем обозначать строчными латинскими буквами.
Заменить совокупности грамматических вхождений, отмечающих состояния автомата, соответствующими символами из Vp.
Полученная таблица представляет собой таблицу функций переходов g(X) LR(0)-анализатора, причем элементы таблицы, соответствующие переходу в пустое множество состояний, имеют значение ОШИБКА.
Для магазинного символа Т, представляющего множество грамматических вхождений Q, и входного символа a значение функции действий f(a) определяется следующим образом.
Если начальное вхождение S0 Î Q и a = e, то f(e) = ДОПУСК.
Если a ¹ e и g(a) ¹ ОШИБКА, то f(a) = ПЕРЕНОС.
Если Xj Î Q – самое правое грамматическое вхождение i-го правила A aXj и a Î FOLLOW(А), то f(a) = (СВЕРТКА, i). Значение остальных элементов таблицы для f(a) – ОШИБКА.
Если имеется множество грамматических вхождений, не удовлетворяющих перечисленным в шаге 4 условиям, то грамматика не принадлежит классу SLR(1).
Если построение f(a) закончено успешно, то грамматика является SLR(1)-грамматикой, а таблица, полученная объединением таблиц, задающих функции f(a) и g(X) – управляющей таблицей T SLR(1)-анализатора.
Конец алгоритма
Построим функцию действий f(a) для грамматики G0, используя шаг 4 алгоритма 8.3.
Начальное вхождение E0 Ex = {E0, E1}, поэтому на основании первого правила шага 4 алгоритма f() = ДОПУСК.
Построим строку f(a), помеченную состоянием Ty:
g(*) = *3 поэтому, используя второе правило построения из шага 4 алгоритма, получаем f(*) = ПЕРЕНОС;
так как грамматическое вхождение T1 Ty = {T1, T3} является самым правым грамматическим вхождением в правило (1) E E + T грамматики, и учитывая, что FOLLOW(E) = {+, ), }, применяя третье правило из шага 4 алгоритма, получаем: f(+) = (СВЕРТКА, 1), f())=(СВЕРТКА, 1), f()=(СВЕРТКА, 1).
Поступая аналогичным образом, получим функцию действия f(a):
-
f(a)
+
(
)
i
П
П
(5
П
П
i6
С, 6
С, 6
С, 6
С, 6
Ex
П
Д
Tx
С, 2
П
С, 2
С, 2
P4
С, 4
С, 4
С, 4
С, 4
Ey
П
П
+1
П
П
3
П
П
)5
С, 5
С, 5
С, 5
С, 5
Ty
С, 1
П
С, 1
С, 1
P3
С, 3
С, 3
С, 3
С, 3
Управляющая таблица (или совокупность SLR(1)-таблиц) SLR(1)-анализатора грамматики G0 приведена на рис. 8.11.
Рис. 8.11. SLR(1)-анализатор для грамматики G0
Рассмотрим работу анализатора, приведенного на рис. 8.11, при выполнении разбора цепочки i + i * i.
Шаг 1. Начальная конфигурация алгоритма (, i + i * i, ).
Алгоритм выбирает строку управляющей таблицы, помеченную символом «» и, основываясь на значениях f(i) = ПЕРЕНОС и g(i) = i6, выполняет перенос и вталкивает в магазин грамматическое вхождение i6, переходя в конфигурацию (i6, + i * i, ).
Шаг 2. Очередной шаг алгоритма определяется строкой управляющей таблицы, помеченной верхним символом магазина «i6».
Функция действий для очередного входного символа «+» имеет значение f(+) = (СВЕРТКА, 6), поэтому должна быть выполнена свертка цепочки в магазине, использующая правило грамматики (6) P i.
Символ, который должен быть помещен в магазин после свертки, определяется строкой таблицы, помеченной символом, находящимся наверху магазина после вычеркивания основы (в данном случае – это «^») и символом правой части основывающего правила (P).
В связи с тем, что g(P) = P4, то алгоритм переходит в конфигурацию (^P4, + i * i, 6).
Продолжая работу, алгоритм проходит следующую последовательность конфигураций:
(^P4, +i*i, 6) |
r6 |
(^P4, +i*i, 6) |
|r4 |
(^Tx, +i*i, 64) |
|
|r2 |
(^Ex, +i*i, 642) |
|s |
(^Ex+1, i*i, 642) |
|
|s |
(^Ex+1i6, *i, 642) |
r6 |
(^Ex+1P4, *i, 6426) |
|
|r4 |
(^Ex+1Ty, *i, 64264) |
|s |
(^Ex+1Ty*3, i, 64264) |
|
|s |
(^Ex+1Ty*3i6, , 64264) |
r6 |
(^Ex+1Ty*3P3, , 642646) |
|
r3 |
(^Ex+1Ty, , 6426463) |
r1 |
(^Ex, , 64264631) |
|
|s |
ДОПУСК |
|
|
Алгоритм достиг состояния ДОПУСК, поэтому входная цепочка i + i * i принадлежит языку, определяемому грамматикой G0, и имеет правый разбор 64264631.
Формулировка задания:
6.2. Построить управляющую таблицу и промоделировать работу SLR(1)-анализатора для КС-грамматики G = < T, N, S, R >.
6.2.2. T = { v, u, w, y }, N = { S, A, B, C }, R = { S Bv, S vC, A u, A vBS, B u, B yw, C Bv, C yAw };
Построение управляющей таблицы:
Построение дополненной грамматики
Дополнительное правило S’S
0 S’S
1 S Bv
2 S vC
3 A u
4 A vBS
5 B u
6 B yw
7 C Bv
8 C yAw
┴OBLOW {S0,B1,v2,u5,y6}
B1 OBLOW {v1}
V2 OBLOW{c2,B7,u5,y6,y8}
V4 OBLOW {B4,u5,y6}
B4 OBLOW {S4,B1,u5,y6,v2}
Y6 OBLOW {w6}
B7 OBLOW {v7}
Y8 OBLOW {A8,u3,v4}
A8 OBLOW {w8}
Таблица отношения OBLOW
|
S0 |
B1 |
V1 |
C2 |
V2 |
A3 |
U3 |
A4 |
V4 |
B4 |
S4 |
B5 |
U5 |
B6 |
Y6 |
W6 |
C7 |
B7 |
V7 |
C8 |
Y8 |
A8 |
W8 |
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V2 |
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
+ |
|
|
+ |
|
|
+ |
|
|
A3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V4 |
|
|
|
|
|
|
|
|
|
+ |
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
B4 |
|
+ |
|
|
+ |
|
|
|
|
|
+ |
|
+ |
|
+ |
|
|
|
|
|
|
|
|
S4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
W6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
V7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y8 |
|
|
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
A8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
W8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
┴ |
+ |
+ |
|
|
+ |
|
|
|
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
На основании таблицы OBLOW построим таблицу переходов конечного автомата
|
S |
A |
B |
C |
u |
v |
w |
y |
S0 |
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
v1 |
|
|
v1 |
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
v2 |
|
|
B7 |
C2 |
u5 |
|
|
y6y8 |
A3 |
|
|
|
|
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
v4 |
|
|
B4 |
|
u5 |
|
|
y6 |
B4 |
S4 |
|
B1 |
|
u5 |
v2 |
|
y6 |
S4 |
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
u5 |
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
y6 |
|
|
|
|
|
|
w6 |
|
w6 |
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
v7 |
|
|
v7 |
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
y8 |
|
A8 |
|
|
u3 |
v4 |
|
|
A8 |
|
|
|
|
|
|
w8 |
|
w8 |
|
|
|
|
|
|
|
|
┴ |
S0 |
|
B1 |
|
u5 |
v2 |
|
y6 |
Преобразуем полученный автомат в детерминированный
|
S |
A |
B |
C |
u |
v |
w |
y |
S0 |
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
V1 |
|
|
v1 |
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
v2 |
|
|
B7 |
C2 |
U5 |
|
|
Y6Y8 |
A3 |
|
|
|
|
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
v4 |
|
|
B4 |
|
U5 |
|
|
Y6 |
B4 |
S4 |
|
B1 |
|
U5 |
V2 |
|
Y6 |
S4 |
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
u5 |
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
y6y8 |
|
A8 |
|
|
U3 |
V4 |
W6 |
|
w6 |
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
V7 |
|
|
v7 |
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
A8 |
|
|
|
|
|
|
W8 |
|
w8 |
|
|
|
|
|
|
|
|
┴ |
S0 |
|
B1 |
|
U5 |
V2 |
|
Y6 |
Определим множество магазинных символов
|
|
S0 |
S0 |
B1 |
B1 |
V1 |
V1 |
C2 |
C2 |
V2 |
V2 |
A3 |
A3 |
U3 |
U3 |
A4 |
A4 |
V4 |
V4 |
B4 |
B4 |
S4 |
S4 |
B5 |
B5 |
U5 |
U5 |
B6 |
B6 |
Y6Y8 |
Yx |
W6 |
W6 |
C7 |
C7 |
B7 |
B7 |
V7 |
V7 |
C8 |
C8 |
A8 |
A8 |
W8 |
W8 |
┴ |
┴ |
Тогда функции переходов имеют вид:
g(X) |
S |
A |
B |
C |
u |
v |
w |
y |
S0 |
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
V1 |
|
|
V1 |
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
V2 |
|
|
B7 |
C2 |
U5 |
|
|
Yx |
A3 |
|
|
|
|
|
|
|
|
U3 |
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
V4 |
|
|
B4 |
|
U5 |
|
|
Yx |
B4 |
S4 |
|
B1 |
|
U5 |
V2 |
|
Yx |
S4 |
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
U5 |
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
Yx |
|
A8 |
|
|
U3 |
V4 |
W6 |
|
W6 |
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
V7 |
|
|
V7 |
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
A8 |
|
|
|
|
|
|
W8 |
|
W8 |
|
|
|
|
|
|
|
|
┴ |
S0 |
|
B1 |
|
U5 |
V2 |
|
Yx |
f(a) |
ε |
u |
v |
w |
y |
S0 |
Д |
|
|
|
|
B1 |
|
|
П |
|
|
V1 |
C1 |
|
|
C1 |
|
C2 |
C2 |
|
|
C2 |
|
V2 |
|
П |
|
|
П |
A3 |
|
|
|
|
|
U3 |
|
|
|
C3 |
|
A4 |
|
|
|
|
|
V4 |
|
П |
|
|
П |
B4 |
|
П |
П |
|
П |
S4 |
|
|
|
C4 |
|
B5 |
|
|
|
|
|
U5 |
|
C5 |
C5 |
|
C5 |
B6 |
|
|
|
|
|
Yx |
|
П |
П |
П |
|
W6 |
|
C6 |
C6 |
|
C6 |
C7 |
|
|
|
|
|
B7 |
|
|
П |
|
|
V7 |
C7 |
C7 |
|
|
|
C8 |
|
|
|
|
|
A8 |
|
|
|
П |
|
W8 |
C8 |
C8 |
|
|
|
┴ |
|
П |
П |
|
П |
Контрольный пример – разбор цепочки vyvuywvw, принадлежащей языку.
(┴, vyvuywvw ,ε)
(┴v2 , yvuywvw, ε)
(┴v2Yx, vuywvw, ε)
(┴v2Yxv4, uywvw , ε)
(┴v2Yxv4u5, ywvw , 5)
(┴v2Yxv4B4, ywvw , 5)
(┴v2Yxv4B4yx, wvw , 5)
(┴v2Yxv4B4yxw, vw , 5)
(┴v2Yxv4B4B1, vw , 56)
(┴v2Yxv4B4B1v1, w ,5 6)
(┴v2Yxv4B4S4, w , 561)
(┴v2YxA8 , w , 5614)
(┴v2YxA8w8, ε, 5614)
(┴v2C2, ε, 56148)
(┴S0, ε, 561482)
ДОПУСК
т.о. правый разбор цепочки vyvuywvw – 561482
Построить управляющую таблицу и промоделировать работу SLR(1)-анализатора для КС-грамматики G = < T, N, S, R >
T = { v, u, w, y }, N = { S, A, B, C }, R = { S ® Bv, S ® vC, A ® u, A ® vBS, B ® u, B ® yw, C ® Bv, C ® yAw };
Построение управляющей таблицы:
Построение дополненной грамматики
Дополнительное правило S’®S
0 S’®S
1 S ® Bv
2 S ® vC
3 A ® u
4 A ® vBS
5 B ® u
6 B ® yw
7 C ® Bv
8 C ® yAw
┴OBLOW {S0,B1,v2,u5,y6}
B1 OBLOW {v1}
V2 OBLOW{c2,B7,u5,y6,y8}
V4 OBLOW {B4,u5,y6}
B4 OBLOW {S4,B1,u5,y6,v2}
Y6 OBLOW {w6}
B7 OBLOW {v7}
Y8 OBLOW {A8,u3,v4}
A8 OBLOW {w8}
Таблица отношения OBLOW
|
S0 |
B1 |
V1 |
C2 |
V2 |
A3 |
U3 |
A4 |
V4 |
B4 |
S4 |
B5 |
U5 |
B6 |
Y6 |
W6 |
C7 |
B7 |
V7 |
C8 |
Y8 |
A8 |
W8 |
S0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 |
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V2 |
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
+ |
|
|
+ |
|
|
+ |
|
|
A3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V4 |
|
|
|
|
|
|
|
|
|
+ |
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
B4 |
|
+ |
|
|
+ |
|
|
|
|
|
+ |
|
+ |
|
+ |
|
|
|
|
|
|
|
|
S4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
W6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
V7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y8 |
|
|
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
A8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
W8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
┴ |
+ |
+ |
|
|
+ |
|
|
|
|
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
|
На основании таблицы OBLOW построим таблицу переходов конечного автомата
|
S |
A |
B |
C |
u |
v |
w |
y |
S0 |
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
v1 |
|
|
v1 |
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
v2 |
|
|
B7 |
C2 |
u5 |
|
|
y6y8 |
A3 |
|
|
|
|
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
v4 |
|
|
B4 |
|
u5 |
|
|
y6 |
B4 |
S4 |
|
B1 |
|
u5 |
v2 |
|
y6 |
S4 |
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
u5 |
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
y6 |
|
|
|
|
|
|
w6 |
|
w6 |
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
v7 |
|
|
v7 |
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
y8 |
|
A8 |
|
|
u3 |
v4 |
|
|
A8 |
|
|
|
|
|
|
w8 |
|
w8 |
|
|
|
|
|
|
|
|
┴ |
S0 |
|
B1 |
|
u5 |
v2 |
|
y6 |
Преобразуем полученный автомат в детерминированный
|
S |
A |
B |
C |
u |
v |
w |
y |
S0 |
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
V1 |
|
|
v1 |
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
v2 |
|
|
B7 |
C2 |
U5 |
|
|
Y6Y8 |
A3 |
|
|
|
|
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
v4 |
|
|
B4 |
|
U5 |
|
|
Y6 |
B4 |
S4 |
|
B1 |
|
U5 |
V2 |
|
Y6 |
S4 |
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
u5 |
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
y6y8 |
|
A8 |
|
|
U3 |
V4 |
W6 |
|
w6 |
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
V7 |
|
|
v7 |
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
A8 |
|
|
|
|
|
|
W8 |
|
w8 |
|
|
|
|
|
|
|
|
┴ |
S0 |
|
B1 |
|
U5 |
V2 |
|
Y6 |
Определим множество магазинных символов
|
|
S0 |
S0 |
B1 |
B1 |
V1 |
V1 |
C2 |
C2 |
V2 |
V2 |
A3 |
A3 |
U3 |
U3 |
A4 |
A4 |
V4 |
V4 |
B4 |
B4 |
S4 |
S4 |
B5 |
B5 |
U5 |
U5 |
B6 |
B6 |
Y6Y8 |
Yx |
W6 |
W6 |
C7 |
C7 |
B7 |
B7 |
V7 |
V7 |
C8 |
C8 |
A8 |
A8 |
W8 |
W8 |
┴ |
┴ |
Тогда функции переходов имеют вид:
g(X) |
S |
A |
B |
C |
u |
v |
w |
y |
S0 |
|
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
V1 |
|
|
V1 |
|
|
|
|
|
|
|
|
C2 |
|
|
|
|
|
|
|
|
V2 |
|
|
B7 |
C2 |
U5 |
|
|
Yx |
A3 |
|
|
|
|
|
|
|
|
U3 |
|
|
|
|
|
|
|
|
A4 |
|
|
|
|
|
|
|
|
V4 |
|
|
B4 |
|
U5 |
|
|
Yx |
B4 |
S4 |
|
B1 |
|
U5 |
V2 |
|
Yx |
S4 |
|
|
|
|
|
|
|
|
B5 |
|
|
|
|
|
|
|
|
U5 |
|
|
|
|
|
|
|
|
B6 |
|
|
|
|
|
|
|
|
Yx |
|
A8 |
|
|
U3 |
V4 |
W6 |
|
W6 |
|
|
|
|
|
|
|
|
C7 |
|
|
|
|
|
|
|
|
B7 |
|
|
|
|
|
V7 |
|
|
V7 |
|
|
|
|
|
|
|
|
C8 |
|
|
|
|
|
|
|
|
A8 |
|
|
|
|
|
|
W8 |
|
W8 |
|
|
|
|
|
|
|
|
┴ |
S0 |
|
B1 |
|
U5 |
V2 |
|
Yx |
f(a) |
ε |
u |
v |
w |
y |
S0 |
Д |
|
|
|
|
B1 |
|
|
П |
|
|
V1 |
C1 |
|
|
C1 |
|
C2 |
C2 |
|
|
C2 |
|
V2 |
|
П |
|
|
П |
A3 |
|
|
|
|
|
U3 |
|
|
|
C3 |
|
A4 |
|
|
|
|
|
V4 |
|
П |
|
|
П |
B4 |
|
П |
П |
|
П |
S4 |
|
|
|
C4 |
|
B5 |
|
|
|
|
|
U5 |
|
C5 |
C5 |
|
C5 |
B6 |
|
|
|
|
|
Yx |
|
П |
П |
П |
|
W6 |
|
C6 |
C6 |
|
C6 |
C7 |
|
|
|
|
|
B7 |
|
|
П |
|
|
V7 |
C7 |
C7 |
|
|
|
C8 |
|
|
|
|
|
A8 |
|
|
|
П |
|
W8 |
C8 |
C8 |
|
|
|
┴ |
|
П |
П |
|
П |
Контрольный пример – разбор цепочки vyvuywvw, принадлежащей языку.
(┴, vyvuywvw ,ε)
(┴v2 , yvuywvw, ε)
(┴v2Yx, vuywvw, ε)
(┴v2Yxv4, uywvw , ε)
(┴v2Yxv4u5, ywvw , 5)
(┴v2Yxv4B4, ywvw , 5)
(┴v2Yxv4B4yx, wvw , 5)
(┴v2Yxv4B4yxw, vw , 5)
(┴v2Yxv4B4B1, vw , 56)
(┴v2Yxv4B4B1v1, w ,5 6)
(┴v2Yxv4B4S4, w , 561)
(┴v2YxA8 , w , 5614)
(┴v2YxA8w8, ε, 5614)
(┴v2C2, ε, 56148)
(┴S0, ε, 561482)
ДОПУСК
т.о. правый разбор цепочки vyvuywvw - 561482
Построить анализатор типа "перенос-свертка" и промоделировать его работу для следующей грамматики простого предшествования
Построить анализатор типа "перенос-свертка" и промоделировать его работу для следующих грамматик слабого предшествования G = < T, N, S, R >
Формулировка задания
Построить анализатор типа "перенос-свертка" и промоделировать его работу для следующих грамматик слабого предшествования G = <T, N, S, R>:
Задание
7.2.2. T = { (, ) }, N = { S, A }, R = { S SA, S A, A (S), A () };
Решение
Определим отношения FIRSTN, LASTN, транзитивные замыкания и отношения (=).
FIRSTN(S) = {S, A} FIRSTN+(S) = {S, A, (}
FIRSTN(A) = {(} FIRSTN+(A) = {(}
LASTN(S) = {A} LASTN+(S) = {A, )}
LASTN(A) = {)} LASTN+(A) = {)}
FIRSTN+
|
LASTN+
|
=
|
Представим отношения в виде булевых матриц:
FIRSTN+ 1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 |
LASTN+ 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 |
= 0 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 |
Опрeделим отношение (<), которое вычисляется как (=)(FIRSTN+):
0 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 |
* |
1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 |
= |
0 0 1 0 0 0 0 0 1 1 1 0 0 0 0 0 |
Вычислим (LASTN+)T, затем ((LASTN+)T)*(=):
(LASTN+)T 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 |
* |
(=) 0 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 |
= |
0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 |
Вычислим (FIRSTN+ + E):
1 1 1 0
0 1 1 0
0 0 1 0
0 0 0 1
Вычислим ((LASTN+)T)*(=) * (FIRSTN+ + E):
0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 |
* |
1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 1 |
= |
0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 |
что соответствует значениям отношения предшествования (>).
Таблица отношений предшествования:
|
S |
A |
( |
) |
ε |
S |
|
= |
< |
= |
|
A |
|
> |
> |
> |
> |
( |
<= |
< |
< |
= |
|
) |
|
> |
> |
> |
> |
┴ |
< |
< |
< |
|
|
Построим таблицу функции переносов:
f(X,a) |
S |
A |
( |
) |
ε |
S |
|
П |
П |
П |
|
A |
|
С |
С |
С |
С |
( |
П |
П |
П |
П |
|
) |
|
С |
С |
С |
С |
┴ |
П |
П |
П |
|
|
┴S |
|
|
|
|
Д |
Построим таблицу функции свёртки
α |
g(α) |
|
X |
β |
|
( |
SA |
1 |
┴ |
SA |
1 |
( |
A |
2 |
┴ |
A |
2 |
( |
(S) |
3 |
┴ |
(S) |
3 |
( |
() |
4 |
┴ |
() |
4 |
Пример разбора цепочки, порождаемой заданной грамматикой предшествования
Цепочка: (())()
(┴,(())(),ε) ->
(┴(,())(),ε) ->
(┴((,))(),ε) ->
(┴((),)(),ε) ->
(┴(A,)(),4) ->
(┴(S,)(),42) ->
(┴(S),(),42) ->
(┴A,(),423) ->
(┴S,(),4232) ->
(┴S(,),4232) ->
(┴S(),ε,4232) ->
(┴SA,ε,42324) ->
(┴S,ε,423241) ->
ДОПУСК
Построить анализатор типа "перенос-свертка" и промоделировать его работу для следующих грамматик слабого предшествования G = < T, N, S, R >
7.2.4. T = { i, or, and, not, (, ) }, N = { S, T, P ), R = { S S or T, S T, T T and P, T P, P i, P ( S ), P not P };
1. Отношение (=) определяется непосредственно из правил грамматики
|
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
S |
|
|
|
|
= |
|
|
|
= |
T |
|
|
|
|
|
= |
|
|
|
P |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
or |
|
= |
|
|
|
|
|
|
|
and |
|
|
= |
|
|
|
|
|
|
not |
|
|
= |
|
|
|
|
|
|
( |
= |
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
┴ |
|
|
|
|
|
|
|
|
|
2. Определим отношения FIRSTN и LASTN
FIRSTN |
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
S |
1 |
1 |
|
|
|
|
|
|
|
T |
|
1 |
1 |
|
|
|
|
|
|
P |
|
|
|
1 |
|
|
1 |
1 |
|
LASTN |
|
|
|
|
|
|
|
|
|
S |
|
1 |
|
|
|
|
|
|
|
T |
|
|
1 |
|
|
|
|
|
|
P |
|
|
1 |
1 |
|
|
|
|
1 |
Построим транзитивные замыкания данных отношений
FIRSTN+ |
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
S |
1 |
1 |
1 |
1 |
|
|
1 |
1 |
|
T |
|
1 |
1 |
1 |
|
|
1 |
1 |
|
P |
|
|
|
1 |
|
|
1 |
1 |
|
LASTN+ |
|
|
|
|
|
|
|
|
|
S |
|
1 |
1 |
1 |
|
|
|
|
1 |
T |
|
|
1 |
1 |
|
|
|
|
1 |
P |
|
|
1 |
1 |
|
|
|
|
1 |
3. Представим отношения в виде булевых матриц, строки и столбцы которых обозначены символами грамматики в порядке S T P i or and not ( )
Тогда матрицу отношения (<•) получим из соотношения (<•) = (=)(FIRSTN+)
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
=
Т.е. отношение (<•) определяется следующим образом
|
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
|S |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
Or |
|
<• |
<• |
<• |
|
|
<• |
<• |
|
and |
|
|
|
<• |
|
|
<• |
<• |
|
Not |
|
|
|
<• |
|
|
<• |
<• |
|
( |
<• |
<• |
<• |
<• |
|
|
<• |
<• |
|
) |
|
|
|
|
|
|
|
|
|
┴ |
|
|
|
|
|
|
|
|
|
матрицу отношения (•>) получим из соотношения (•>) =((LASTN+)T) (=)(E+FIRSTN+)
(LASTN+)=
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
(LASTN+)T=
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
((LASTN+)-1)(=) =
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
(E+FIRTSN+) =
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Значит матрица отношений предшествования для данной грамматики выглядит следующим образом
|
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
ε |
|S |
|
|
|
|
= |
|
|
|
= |
•> |
T |
|
|
|
|
|
= |
|
|
|
•> |
P |
|
|
|
|
|
|
|
|
|
•> |
i |
|
|
|
|
|
|
|
|
|
•> |
or |
|
<•= |
<• |
<• |
|
|
<• |
<• |
|
|
and |
|
|
= |
<• |
|
|
<• |
<• |
|
|
not |
|
|
= |
<• |
|
|
<• |
<• |
|
|
( |
<•= |
<• |
<• |
<• |
|
|
<• |
<• |
|
|
) |
|
|
|
|
|
|
|
|
|
•> |
┴ |
<• |
<• |
<• |
<• |
|
|
<• |
<• |
|
|
Используя таблицу отношений предшествования построим функцию переноса
|
S |
T |
P |
i |
or |
and |
not |
( |
) |
ε |
|S |
|
|
|
|
П |
|
|
|
П |
С |
T |
|
|
|
|
С |
П |
|
|
С |
С |
P |
|
|
|
|
С |
С |
|
|
С |
С |
i |
|
|
|
|
С |
С |
|
|
С |
С |
or |
|
П |
П |
П |
|
|
П |
П |
|
|
and |
|
|
П |
П |
|
|
П |
П |
|
|
not |
|
|
П |
П |
|
|
П |
П |
|
|
( |
П |
П |
П |
П |
|
|
П |
П |
|
|
) |
|
|
|
|
С |
С |
|
|
С |
С |
┴ |
П |
П |
П |
П |
|
|
П |
П |
|
|
┴S |
|
|
|
|
|
|
|
|
|
Д |
И функцию свертки
X |
β |
g(α) |
┴ |
S or T |
1 |
┴ |
T |
2 |
( |
S or T |
1 |
( |
T |
2 |
┴ |
T and P |
3 |
┴ |
P |
4 |
( |
T and P |
3 |
( |
P |
4 |
or |
T and P |
3 |
or |
P |
4 |
┴ |
i |
5 |
┴ |
(S) |
6 |
┴ |
Not P |
7 |
( |
i |
5 |
( |
(S) |
6 |
( |
Not P |
7 |
or |
i |
5 |
or |
(S) |
6 |
or |
Not P |
7 |
and |
i |
5 |
and |
(S) |
6 |
and |
Not P |
7 |
not |
i |
5 |
not |
(S) |
6 |
not |
Not P |
7 |
Контрольный пример - разбор цепочки (not i ) and i or not i, принадлежащей языку
(┴, (not i ) and i or not I,ε)
(┴ ( , not i ) and i or not I, ε)
(┴ (not, i ) and i or not I, ε)
(┴ (not i,) and i or not I, ε)
(┴ (not P , ) and i or not I,5)
(┴ (P , ) and i or not I,57)
(┴ (T ,) and i or not I,574)
(┴ (S ,) and i or not I,5742)
(┴ (S) , and i or not I,5742)
(┴P, and i or not I,57426)
(┴T , and i or not I,574264)
(┴Tand, i or not I,574264)
(┴Tand I, or not I,574264)
(┴Tand P , or not I,5742645)
(┴T , or not I,57426453)
(┴S , or not i,574264532)
(┴Sor , not I,574264532)
(┴Sor not , I,574264532)
(┴Sor not I , ε,574264532)
(┴Sor not P , ε,5742645325)
(┴Sor P, ε,57426453257)
(┴Sor T , ε,574264532574)
(┴S, ε, 5742645325741)
ДОПУСК
Построить анализатор типа "перенос-свертка" и промоделировать его работу для следующих грамматик слабого предшествования G = < T, N, S, R >
7.2.4. T = { i, or, and, not, (, ) }, N = { S, T, P ), R = { S ® S or T, S ® T, T ® T and P, T ® P, P ® i, P ® ( S ), P ® not P };
1. Отношение (=) определяется непосредственно из правил грамматики
|
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
S |
|
|
|
|
= |
|
|
|
= |
T |
|
|
|
|
|
= |
|
|
|
P |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
or |
|
= |
|
|
|
|
|
|
|
and |
|
|
= |
|
|
|
|
|
|
not |
|
|
= |
|
|
|
|
|
|
( |
= |
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
┴ |
|
|
|
|
|
|
|
|
|
2. Определим отношения FIRSTN и LASTN
FIRSTN |
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
S |
1 |
1 |
|
|
|
|
|
|
|
T |
|
1 |
1 |
|
|
|
|
|
|
P |
|
|
|
1 |
|
|
1 |
1 |
|
LASTN |
|
|
|
|
|
|
|
|
|
S |
|
1 |
|
|
|
|
|
|
|
T |
|
|
1 |
|
|
|
|
|
|
P |
|
|
1 |
1 |
|
|
|
|
1 |
Построим транзитивные замыкания данных отношений
FIRSTN+ |
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
S |
1 |
1 |
1 |
1 |
|
|
1 |
1 |
|
T |
|
1 |
1 |
1 |
|
|
1 |
1 |
|
P |
|
|
|
1 |
|
|
1 |
1 |
|
LASTN+ |
|
|
|
|
|
|
|
|
|
S |
|
1 |
1 |
1 |
|
|
|
|
1 |
T |
|
|
1 |
1 |
|
|
|
|
1 |
P |
|
|
1 |
1 |
|
|
|
|
1 |
3. Представим отношения в виде булевых матриц, строки и столбцы которых обозначены символами грамматики в порядке S T P i or and not ( )
Тогда матрицу отношения (<•) получим из соотношения (<•) = (=)(FIRSTN+)
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
=
Т.е. отношение (<•) определяется следующим образом
|
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
|S |
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
Or |
|
<• |
<• |
<• |
|
|
<• |
<• |
|
and |
|
|
|
<• |
|
|
<• |
<• |
|
Not |
|
|
|
<• |
|
|
<• |
<• |
|
( |
<• |
<• |
<• |
<• |
|
|
<• |
<• |
|
) |
|
|
|
|
|
|
|
|
|
┴ |
|
|
|
|
|
|
|
|
|
матрицу отношения (•>) получим из соотношения (•>) =((LASTN+)T) (=)(E+FIRSTN+)
(LASTN+)=
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
(LASTN+)T=
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
((LASTN+)-1)(=) =
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
(E+FIRTSN+) =
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Значит матрица отношений предшествования для данной грамматики выглядит следующим образом
|
S |
T |
P |
I |
Or |
And |
Not |
( |
) |
ε |
|S |
|
|
|
|
= |
|
|
|
= |
•> |
T |
|
|
|
|
|
= |
|
|
|
•> |
P |
|
|
|
|
|
|
|
|
|
•> |
i |
|
|
|
|
|
|
|
|
|
•> |
or |
|
<•= |
<• |
<• |
|
|
<• |
<• |
|
|
and |
|
|
= |
<• |
|
|
<• |
<• |
|
|
not |
|
|
= |
<• |
|
|
<• |
<• |
|
|
( |
<•= |
<• |
<• |
<• |
|
|
<• |
<• |
|
|
) |
|
|
|
|
|
|
|
|
|
•> |
┴ |
<• |
<• |
<• |
<• |
|
|
<• |
<• |
|
|
Используя таблицу отношений предшествования построим функцию переноса
|
S |
T |
P |
i |
or |
and |
not |
( |
) |
ε |
|S |
|
|
|
|
П |
|
|
|
П |
С |
T |
|
|
|
|
С |
П |
|
|
С |
С |
P |
|
|
|
|
С |
С |
|
|
С |
С |
i |
|
|
|
|
С |
С |
|
|
С |
С |
or |
|
П |
П |
П |
|
|
П |
П |
|
|
and |
|
|
П |
П |
|
|
П |
П |
|
|
not |
|
|
П |
П |
|
|
П |
П |
|
|
( |
П |
П |
П |
П |
|
|
П |
П |
|
|
) |
|
|
|
|
С |
С |
|
|
С |
С |
┴ |
П |
П |
П |
П |
|
|
П |
П |
|
|
┴S |
|
|
|
|
|
|
|
|
|
Д |
И функцию свертки
X |
β |
g(α) |
┴ |
S or T |
1 |
┴ |
T |
2 |
( |
S or T |
1 |
( |
T |
2 |
┴ |
T and P |
3 |
┴ |
P |
4 |
( |
T and P |
3 |
( |
P |
4 |
or |
T and P |
3 |
or |
P |
4 |
┴ |
i |
5 |
┴ |
(S) |
6 |
┴ |
Not P |
7 |
( |
i |
5 |
( |
(S) |
6 |
( |
Not P |
7 |
or |
i |
5 |
or |
(S) |
6 |
or |
Not P |
7 |
and |
i |
5 |
and |
(S) |
6 |
and |
Not P |
7 |
not |
i |
5 |
not |
(S) |
6 |
not |
Not P |
7 |
Контрольный пример - разбор цепочки (not i ) and i or not i, принадлежащей языку
(┴, (not i ) and i or not I,ε)
(┴ ( , not i ) and i or not I, ε)
(┴ (not, i ) and i or not I, ε)
(┴ (not i,) and i or not I, ε)
(┴ (not P , ) and i or not I,5)
(┴ (P , ) and i or not I,57)
(┴ (T ,) and i or not I,574)
(┴ (S ,) and i or not I,5742)
(┴ (S) , and i or not I,5742)
(┴P, and i or not I,57426)
(┴T , and i or not I,574264)
(┴Tand, i or not I,574264)
(┴Tand I, or not I,574264)
(┴Tand P , or not I,5742645)
(┴T , or not I,57426453)
(┴S , or not i,574264532)
(┴Sor , not I,574264532)
(┴Sor not , I,574264532)
(┴Sor not I , ε,574264532)
(┴Sor not P , ε,5742645325)
(┴Sor P, ε,57426453257)
(┴Sor T , ε,574264532574)
(┴S, ε, 5742645325741)
ДОПУСК
Построить анализатор типа "перенос-свертка" и промоделировать его работу для следующих грамматик операторного предшествования G=<T,N,S,R>

