18. Геометрические характеристики плоских сечений Общие сведения

Как было показано выше, при растяжении и сжатии площадь поперечного сечения полностью характеризует прочность и жесткость стержня. Возьмем некоторое поперечное сечение бруса (рис. 4.1). Если представить себе сечение состоящим из бесчисленного м ножества площадок dF, то площадь всего сечения  . Площадь является простейшей геометрической характеристикой сечения, имеет размерность L². Отметим два важных свойства: площадь всегда положительна и не зависит от выбора системы координат.

При расчетах на изгиб, кручение, сложное сопротивление и устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции сечений, которые зависят не только от формы и размеров сечений, но также от положения осей и точек (полюсов), относительно которых они вычисляются.

 Рис.4.1

Статическим моментом S_x сечения относительно оси х называется геометрическая характеристика, определяемая интегралом вида

,                                            (4.1)

где у - расстояние от элементарной площадки dF до оси х.

Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической  механики теореме Вариньона о моменте равнодействующей можно написать

,                              (4.2)

где площадь сечения F представляет собой равнодействующую, координата у_с - плечо равнодействующей, с - центр тяжести сечения.

Аналогично, статический момент относительно оси у равен

,                             (4.3)

откуда следуют формулы для определения координат центра тяжести

                               (4.4)

Статические моменты могут быть положительными, отрицательными и равными нулю. В частности, относительно любых центральных осей (проходящих через центр тяжести С обозначаются х_с, у_с) статические моменты  . Размерность статических моментов L³. Для сложного сечения, состоящего из n частей, выражения (4.2), (4.3) можно представить в виде

                                  (4.5)

где   - статические моменты i-й части сечения относительно осей х и у соответственно.

Таким образом, статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей сечения относительно той же оси.

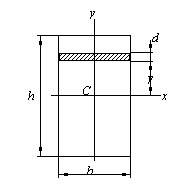
Прямоугольник

Определим момент инерции сечения относительно оси х₀, проходящей через центр тяжести прямоугольника высотой h и шириной b параллельно основанию (рис.4.5). Выделим из прямоугольника линиями, параллельными оси х элементарную полоску высотой dу и шириной b. Площадь этой полоски dF=bdx, расстояние от полоски до оси х равно у. Подставим эти величины в выражение момента инерции относительно оси х (4.6):

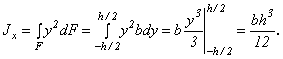
.                         (4.11)

Аналогично, получим:

.                        (4.12)

 

 

Очевидно, что

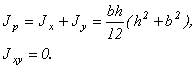
Треугольник

Определим момент инерции треугольника относительно оси х₁, проходящей через основание.

.

Элементарная площадка  .

Из подобия треугольников получаем:

,

где b – основание треугольника, h – его высота.

Таким образом

Расстояние от основания треугольника до центра тяжести равно

.

По формуле переноса находим момент инерции относительно центральной оси х, параллельно основанию

.

                         Круг

Определим сначала полярный момент инерции относительно центра круга (рис.4.7). За dF примем площадь бесконечно тонкого кольца толщиной d , расположенного на расстоянии  от центра к руга  .

Тогда

 

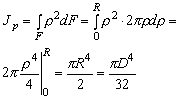
                 Рис.4.7

           (4.13)

Теперь определим осевые моменты инерции. Очевидно, что в силу симметрии  ; но  . Откуда

.                               (4.14)

Кольцо

Определим моменты инерции кольца, у которого R - наружный радиус, r - внутренний радиус (рис.4.8). Интегрируя полученное ранее выражение для полярного момента инерции в пределах от r до R, получим

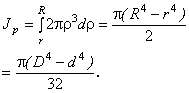
Это выражение может быть представлено в виде

                 

                   Рис.4.8

                                                                                                                                                 ,                                               (4.15)

где  .

Соответственно