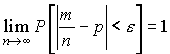- •Методические указания к Госам Автор Юршевич м.С и Потылицын в.П. Оглавление
- •Вопрос№1 Корни и канонические разложения многочленов над полями вещественных и комплексных чисел. Неприводимые многочлены над полями r и c.
- •Вопрос№2 Теоремы об а)умножении определителей и б)о ранге матрицы.
- •Вопрос№3 а)Правило Крамера, б)Th Кронекера-Капелли и в)Th-мы об однородных уравнениях.
- •Вопрос№4 Скалярное, векторное и смешанное произведение векторов. B) Линейные и унитарные пространства, базы, размерность, подпространства.
- •Вопрос№5 а)Линейное преобразование, его б)матрицы, в)характеристические корни, собственные значения и собственные векторы. Г)Жорданова форма матрицы.
- •Вопрос№6 а)Уравнения прямых и плоскостей в пр-стве. Канонические уравнения б) кривых и в) поверхностей 2-го порядка.
- •Вопрос№8 Th о функциональной полноте ив.
- •Вопрос№9 а)предел посл-сти и б)предел ф-ции в точке.
- •Вопрос№10 Непрерывность ф-ции а) в точке и на отрезке, б) точки разрыва 1-го и 2-го рода.
- •Вопрос№11 Дифференцируемость и дифференциалы ф-ций 1-й и многих переменных. Инвариантность формы 1-го дифференциала.
- •Дифференциал функции многих переменных.
- •Теорема об инвариантной форме первого дифференциала.
- •Вопрос№12 Формула Лагранжа конечных прирашений.
- •Вопрос№13 Формула Тейлора с остаточным членом в формах Пеано и Лагранжа.
- •Вопрос№14
- •Вопрос№15 Числовые и функциональные последовательности и ряды. Равномерная сходимость.
- •Сходимость функциональных последовательностей и рядов
- •Равномерная сходимость
- •Вопрос №16 Теория о неявной функции
- •Вопрос№17 а) Градиент, касательная пл-сть и нормаль в точке поверхности. Б) Уравнения касательной и нормали к кривой.
- •Вопрос№19
- •Определенный интеграл.
- •Вопрос№20 Формула Ньютона-Лейбница
- •Вопрос№21 Кратные интегралы. Теорема Фубини. Поверхностные и криволинейные интегралы. Формулы Грина, Остроградского, Стокса.
- •Вопрос№23 Разложение функции по ортогональной системе функций, ряд Фурье, условие замкнутости ортогональной системы (равенство Парсеваля-Стеклова).
- •Вопрос№24 Метрика, метрическое пространство. Открытые и замкнутые множества.
- •Вопрос№25 Фундаментальная последовательность, полное пространство.
- •Вопрос№26 Принцип сжимающих отображений.
- •Вопрос№27 Компактное пространство и множество. Критерий компактности в .
- •Вопрос№29 Определение голоморфной функции, уравнения Коши-Римана.
- •Уравнение Коши-Римана
- •Вопрос№30 Интегральная теорема Коши. Интегральная формула Коши.
- •Вопрос№32_1 а) Классификация изолированных особых точек. Б)Теорема о вычетах. В)Ряд Лорана. Д)Теорема Руше и принцип аргумента.
- •Вопрос№32_2
- •Вопрос№33_1 ду простейших типов и их инегрирование.
- •Вопрос№34 Теорема Коши-Пикара существования и единственности решения ду 1-го порядка.
- •Для любой внутренней точки найдется решение уравнения (8.2.2), удовлетворяющее условию при .
- •Если два решения и уравнения (8.2.2) совпадают хотя бы для одного значения , т.Е. , то эти решения совпадают для всех .
- •Вопрос№35 Линейные ду n-го порядка с постоянными коэффициентами.
- •Вопрос№36_1 Устойчивость решения линейных систем ду 2-го порядка. Классификация особых точек (узел, седло, фокус, центр и тд.)
- •Вопрос№36_2
- •Критерий Гурвица
- •Вопрос№37 Классификация ду в частных производных 2-го порядка.
- •Вопрос№39 Метод разделения переменных.
- •Вопрос№41 Точные методы решения систем линейных алгебраических уравнений: метод исключения Гаусса, метод исключения с выбором главного элемента. Сравнение методов.
- •Вопрос№42 Метод простой итерации решения систем линейных алгебраических уравнений. Условие сходимости.
- •Вопрос№43 Метод простой итерации вычисления корня нелинейного уравнения. Условие сходимости. Метод Ньютона: формула, геометрическая интерпретация, условия сходимости.
- •Вопрос№44
- •Вопрос№45_1 Явная схема краевой задачи для уравнения теплопроводности. Аппроксимация. Гармонический анализ.
- •Вопрос№45_2
- •Гармонический анализ.
- •Вопрос№47 Понятие корректности, устойчивости и сходимости разностной задачи. Теорема эквивалентности.
- •Вопрос№48 Классификация интерфейсов вычислительных систем.
- •Вопрос№49 Основные функции операционной системы.
- •Вопрос№50
- •Вопрос№51_1 Алгоритмы сортировок (элементарные методы сортировки, быстрая сортировка Хоара, сортировка слиянием), поиска, рекурсий.
- •Сортировка Выбором
- •Сортировка Вставкой
- •Пузырьковая Сортировка
- •Быстрая сортировка
- •Слияние
- •Вопрос№51_2
- •Рекурсия
- •Вопрос№52 Основы объектно-ориентированного программирования. (инкапсул., полиморфизм, наследов.)
- •Вопрос№53 Симплекс метод. Постановка задачи. Способы решения Каноническая форма:
- •Вопрос№54_1 Матричные игры. Решение игры в смешанных стратегиях.
- •Вопрос№54_2
- •Теорема(Джона Фон Неймана)
- •Вопрос№55 Основные требования к организации баз данных как хранилищ корпоративно используемых данных. Способы и средства достижения этих требований.
- •Вопрос№56_1 Технология проектирования баз данных: этапы проектирования, модели представления предметной области, синтаксические модели данных. Этапы разработки базы данных
- •Вопрос№56_2
- •Вопрос№57 Классическое определение вероятности. Условная вероятность, независимые события, теоремы сложения и умножения.
- •Теорема сложения
- •Вопрос№58 Дискретные и непрерывные случайные величины, определения и свойства функции и плотности распределения.
- •Вопрос№59 Математическое ожидание и дисперсия случайной величины. Моменты.
- •Своиства
- •Вопрос№60 Сходимость по вероятности, неравенство Чебышева, закон больших чисел в формах Чебышева и Бернулли.
- •Вопрос№61 Точечные статистические оценки: несмещенность, состоятельность, эффективность. Определение и свойства выборочного среднего и выборочной дисперсии.
- •Практика Диффуры.
- •1.Найти частное решение уравнения в точке .
- •3. Алгоритм нахождения собственных значений и собственных векторов
- •5. Рассмотрим несколько примеров несобственных интегралов первого рода.
- •6.Рассмотрим несколько примеров на вычисление несобственных интегралов второго рода.
- •7.Рассмотрим примеры использования признака сравнения несобственных интегралов.
- •9. Вычисление пределов. (правили Лопиталя)
- •11.Исследовать функцию и построить ее график.
- •12. Исследовать функцию и построить ее график.
- •13. Исследовать функцию и построить ее график.
- •15. Найти полный дифференциал функции
- •16. Найти уравнения касательной плоскости и нормали к поверхности
- •19. Вычисление двойных интегралов
- •20. Вычислить интеграл
- •22. Найти общее решение дифференциального уравнения .
- •23. Уравнения с разделяющимися переменными.
- •24. Уравнения, приводящиеся к однородным.
- •Разделяем переменные:
- •25.Решить уравнение
- •26. Решить уравнение
- •28. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.
- •29.Решить уравнение
- •30. Найти общее решение системы уравнений:
- •31. Сходимость рядов.
- •32. Теория вычетов
- •33. Криволинейные интегралы
- •34.Устойчивость оду
- •35.Даны вершины треугольника a(1,-2,-4), b(3,1,-3), c(5,1,-7). Составить уравнение высоты, проведенной из вершины b. И вычислить площадь.
- •36.Проверить компланарны ли вектора a(2,0,1), b(5.3.-3), c(3,3,10).
Своиства
1°. Математическое ожидание постоянной С равно этой постоянной. 2°. Постоянный множитель можно выносить за знак математического ожидания, т.е.
![]()
3°. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин:
|
(41) |
4°. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин **:
|
(42) |
* в случае, если множество
возможных значений дискретной случайной
величины образует бесконечную
последовательность x1,
x2,
..., xn,
..., то математическое ожидание этой
случайной величины определяется как
сумма ряда
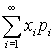 причем
требуется, чтобы этот ряд абсолютно
сходился.
Дисперсией
причем
требуется, чтобы этот ряд абсолютно
сходился.
Дисперсией
![]() случайной
величины
называется
математическое ожидание квадрата
отклонения случайной величины от ее
математичекого ожидания *:
случайной
величины
называется
математическое ожидание квадрата
отклонения случайной величины от ее
математичекого ожидания *:
|
(43) |
Рассмотрим теперь свойства дисперсии.
1°. Дисперсия постоянной равна нулю. 2°. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
|
(47) |
3°.
Если
и
![]() -
независимые случайные
величины , то дисперсия суммы этих
величин равна сумме их дисперсий:
-
независимые случайные
величины , то дисперсия суммы этих
величин равна сумме их дисперсий:
|
(48) |
Начальным моментом порядка k случайной величины ξ называется число α_k=M(ξ)^k.
Центральным моментом порядка k случайной величины ξ называется число μ_k=M(ξ-Mξ)^k.
Вопрос№60 Сходимость по вероятности, неравенство Чебышева, закон больших чисел в формах Чебышева и Бернулли.
Последовательность ξ1,ξ2,…сходится по вероятности к ξ (ξ_n→¯pξ), если для любого ε>0 lim(n→∞)p(|ξ_n-ξ|>ε) = 0.
Неравенство
Чебышева. Пусть
—
случайная величина, а
![]() -
положительное число. Тогда вероятность
того, что модуль отклонения случайной
величины.
от
ее математического ожидания окажется
меньше, чем
,
больше или равна разности
-
положительное число. Тогда вероятность
того, что модуль отклонения случайной
величины.
от
ее математического ожидания окажется
меньше, чем
,
больше или равна разности
|
(52) |
Неравенство (52) называется неравенством Чебышева
Закон
больших чисел Чебышева.
Имеет
место следующее утверждение. Пусть![]() - последовательность попарно независимых
случайных величин, имеющих ограниченные
в совокупности дисперсии, т. е.
- последовательность попарно независимых
случайных величин, имеющих ограниченные
в совокупности дисперсии, т. е.
![]() для
любого i. Тогда, каково бы нибыло
для
любого i. Тогда, каково бы нибыло
![]() ,
справедливо соотношение
,
справедливо соотношение
|
Смысл
закона больших чисел Чебышева состоит
в следующем. В то время как отдельная
случайная величина может принимать
значения, очень далекие от своего
математического ожидания, средняя
арифметическая большого числа случайных
величин с вероятностью, близкой к
единице, принимает значение, мало
отличающееся от среднего арифметического
их математических ожиданий.
Закон
больших чисел Бернулли.
Пусть производится
последовательность независимых
испытаний, в результате каждого из
которых может наступить или не наступить
событие А,
причем вероятность наступления этого
события одна и та же при каждом испытании
и равна р.
Если событие А
фактически произошло m
раз в n
испытаниях, то отношение m/n
называют, как мы знаем, частотой появления
события А.
Частота есть случайная величина, причем
вероятность того, что частота принимает
значение m/n,
выражается по формуле Бернулли (13):
![]()
Закон больших чисел в форме Бернулли состоит в следующем: с вероятностью, сколь угодно близкой к единице, можно утверждать, что при достаточно большом числе опытов частота появления события А как угодно мало отличается от его вероятности, т. е.
|
(55) |
иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А).