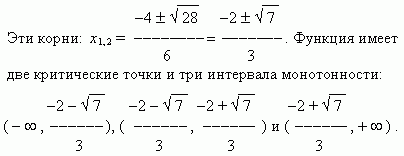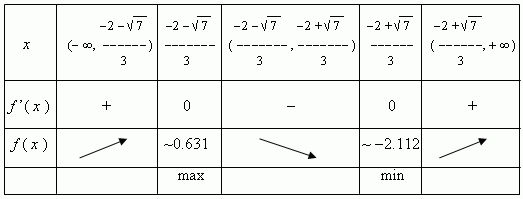|
|
График
1.3.6.1.
Предел
функции y = x2 при x → 2.
|
График
1.3.6.2.
Предел
функции 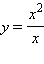 при x → 0.
при x → 0.
|
Если A –
предел функции в точке a,
то пишут, что
Определения предела функции по Коши и
по Гейне эквивалентны.
|
График
1.3.6.3.
Предел
функции y = {x (x ≠ 0); 1 (x = 0)} приx → 0 равен 0.
|
Предел
функции 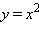 в
точке a = 0 равен
0:
в
точке a = 0 равен
0: 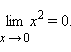 Предел
функции
в
точке a = 0 также
равен 0, хотя эта функция не существует
в этой точке (ее знаменатель обращается
в нуль). Предел функции
Предел
функции
в
точке a = 0 также
равен 0, хотя эта функция не существует
в этой точке (ее знаменатель обращается
в нуль). Предел функции  в
точке a = 0 равен
0, хотя значение функции в этой
точке f (0) = 1.
в
точке a = 0 равен
0, хотя значение функции в этой
точке f (0) = 1.
5)Многочлен. Предел многочлена
на бесконечности
МНОГОЧЛЕН (полином),
сумма одночленов, которые являются
произведениями, состоящими из числового
множителя (коэффициента) и одной или
нескольких букв, каждая из которых
взята с тем или иным показателем степени.
В общем виде, многочлен имеет форму
Pn(x)=аnхn+an-1xn-1+аn-2хn-2+....+а2х2+a1х+а0,
где а0....аn-1,
аn -
КОЭФФИЦИЕНТЫ многочлена. Степенью
многочлена является самый высокий
показатель степени в этой сумме с
ненулевым коэффициентом. Например,
Р4(х)=2x4-3x3+x2+х+5
является многочленом со степенью
четыре. В этом примере значения многочлена
при х=0; 1 и 2 равны Р4(0)=5,
Р4(1)=6,
Р4(2)=19
соответственно. Многочлен может быть
представлен графически, путем отметки
значения у=Рn(х)
на графике в соответствии со значениями
х.
ДОДЕЛАТЬ !!!
6) Односторонние
пределы функции при х →
х◦
(при х ≠ 0 или +/- 0 – не понятно
написано!)
ОДНОСТОРОННИЙ
ПРЕДЕЛ
Односторо́нний
преде́л в математическом
анализе — предел
числовой функции,
подразумевающий «приближение» к
предельной точке с одной стороны. Такие
пределы называют соответственно левосторо́нним
преде́лом (или преде́лом
сле́ва)
и правосторо́нним
преде́лом (преде́лом
спра́ва).
-
предел функции в нек-рой точке справа
или слева. Пусть f - отображение
упорядоченного множества X(напр.,
множества, лежащего на числовой прямой),
рассматриваемого как топологич.
пространство с топологией, порожденной
отношением порядка, в топологич.
пространство Y и  .
Предел отображения f по любому
интервалу
.
Предел отображения f по любому
интервалу 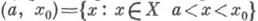 наз.
пределом слева отображения f и обозначают
наз.
пределом слева отображения f и обозначают
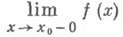
(он
не зависит от выбора 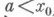 ),
а предел по интервалу
),
а предел по интервалу 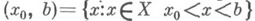 наз.
пределом справа и обозначают
наз.
пределом справа и обозначают
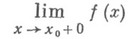
(он
не зависит от выбора 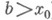 ).
Если точка
).
Если точка 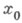 является
предельной как слева, так и справа для
множества определения функции f, то
обычный предел
является
предельной как слева, так и справа для
множества определения функции f, то
обычный предел
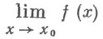
по
проколотой окрестности точки х 0 (в
этом случае его наз. также двусторонним,
в отличие от односторонних пределов)
существует тогда и только тогда, когда
в точке х 0 существуют
пределы слева и справа и они равны между
собой.
7) Теорема
о сущ-нии предела функции в тчк
8)
Сравнение бесконечно
малых функций
Как известно,
сумма, разность и произведение двух
б.м.ф. есть функция бесконечно малая.
Отношение же двух б.м.ф. может вести
себя различным образом: быть конечным
числом, быть бесконечно большой функцией,
бесконечно малой или вообще не стремиться
ни к какому пределу.
Две б.м.ф.
сравниваются между собой с помощью их
отношения.
Пусть
α=α(х) и ß=ß(х) есть б.м.ф. при х→хо,
т. е.
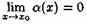 и
и 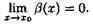
1.
Если 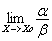 =А 0
(АєR), то α и ß называются бесконечно
малыми одного порядка.
=А 0
(АєR), то α и ß называются бесконечно
малыми одного порядка.
2.
Если,
=0,
то α називатся бесконечно малой более
высокого порядка , чем ß.
3.
Если
=∞,
то α называется бесконечно малой более
низкого порядка, чем ß.
4.
Если
не
существует, то α и ß называются
несравнимыми бесконечно малыми.
Отметим,
что таковы же правила сравнения б.м.ф.
при х →±∞, х →х0±0.
<< Пример
18.1<
Сравнить
порядок функций α=3х2 и
ß=14х2 при
х→0
9)
Эквивалентные функции и
их св-ва.
Сравнение
бесконечно малых функций
Как
известно, сумма, разность и произведение
двух б.м.ф. есть функция бесконечно
малая. Отношение же двух б.м.ф. может
вести себя различным образом: быть
конечным числом, быть бесконечно большой
функцией, бесконечно малой или вообще
не стремиться ни к какому пределу.
Две
б.м.ф. сравниваются между собой с помощью
их отношения.
Пусть
α=α(х) и ß=ß(х) есть б.м.ф. при х→хо,
т. е.
и
1.
Если
=А 0
(АєR), то α и ß называются бесконечно
малыми одного порядка.
2.
Если,
=0,
то α називатся бесконечно малой более
высокого порядка , чем ß.
3.
Если
=∞,
то α называется бесконечно малой более
низкого порядка, чем ß.
4.
Если
не
существует, то α и ß называются
несравнимыми бесконечно малыми.
Отметим,
что таковы же правила сравнения б.м.ф.
при х →±∞, х →х0±0.
Свойство:
1) ~ , 
2) Если ~ и ~ ,
то ~ , 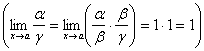
3) Если ~ ,
то ~ , 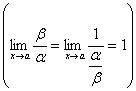
4)
Если ~ 1 и ~ 1 и 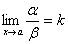 ,
то и
,
то и 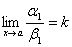 или
или 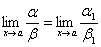 .
.
Следствие:
а) если ~ 1 и
,
то и 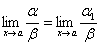
б) если ~ 1 и
,
то 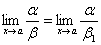
Свойство 4 особенно важно на практике,
т.к. оно фактически означает, что предел
отношения бесконечно малых не меняется
при замене их на эквивалентные бесконечно
малые. Этот факт дает возможность при
нахождении пределов заменять бесконечно
малые на эквивалентные им функции, что
может сильно упростить вычисление
пределов.
10. Замечательные
пределы.
Определение 2.11
Первым замечательным пределом называется
предел
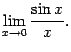
Теорема 2.14 Первый
замечательный предел равен 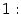

Доказательство.
Рассмотрим два односторонних
предела 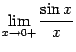 и
и 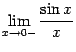 и
докажем, что каждый из них равен 1. Тогда
потеореме
2.1 двусторонний
предел
и
докажем, что каждый из них равен 1. Тогда
потеореме
2.1 двусторонний
предел 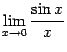 также
будет равняться 1.
также
будет равняться 1.
Итак,
пусть  (этот
интервал -- одно из окончаний базы
(этот
интервал -- одно из окончаний базы  ).
В тригонометрическом круге (радиуса
).
В тригонометрическом круге (радиуса  )
с центром
)
с центром 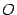 построим
центральный угол, равный
построим
центральный угол, равный 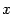 ,
и проведём вертикальную касательную
в точке
,
и проведём вертикальную касательную
в точке  пересечения
горизонтальной оси с окружностью (
пересечения
горизонтальной оси с окружностью (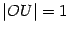 ).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой
).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой 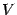 ,
а с вертикальной касательной --
буквой
,
а с вертикальной касательной --
буквой  ;
через
;
через  обозначим
проекцию точки
на
горизонтальную ось.
обозначим
проекцию точки
на
горизонтальную ось.
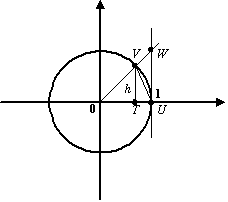
Рис.2.27.Тригонометрический
круг
Пусть 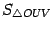 --
площадь треугольника
--
площадь треугольника 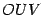 ,
,  --
площадь кругового сектора
,
а
--
площадь кругового сектора
,
а 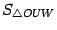 --
площадь треугольника
--
площадь треугольника 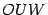 .
Тогда очевидно следующее неравенство:
.
Тогда очевидно следующее неравенство:
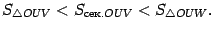
Заметим,
что горизонтальная координата
точки
равна 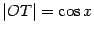 ,
а вертикальная --
,
а вертикальная -- 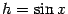 (это
высота треугольника
),
так что
(это
высота треугольника
),
так что 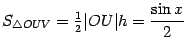 .
Площадь центрального сектора круга
радиуса
.
Площадь центрального сектора круга
радиуса  с
центральным углом
равна
с
центральным углом
равна 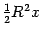 ,
так что
,
так что  .
Из треугольника
находим,
что
.
Из треугольника
находим,
что 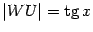 .
Поэтому
.
Поэтому 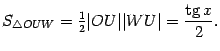 Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
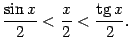
Все
три части этого неравенства положительны,
поэтому его можно записать так:

или
(умножив на  )
так:
)
так:
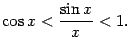
Предел
постоянной 1 в правой части неравенства,
очевидно, равен 1. Если мы покажем, что
при
предел 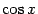 в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части
в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части 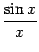 также
будет равен 1.
также
будет равен 1.
Итак,
осталось доказать, что 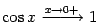 .
Сперва заметим, что
.
Сперва заметим, что 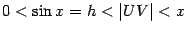 ,
так как
равняется
длине дуги окружности
,
так как
равняется
длине дуги окружности 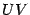 ,
которая, очевидно, длиннее хорды
,
которая, очевидно, длиннее хорды 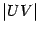 .
Применяя теорему "о двух милиционерах"
к неравенству
.
Применяя теорему "о двух милиционерах"
к неравенству
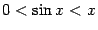
при
,
получаем, что
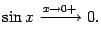
|
(2.3)
|
Простая
замена переменной 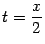 показывает,
что и
показывает,
что и 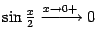 .
Теперь заметим, что
.
Теперь заметим, что 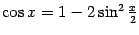 .
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
.
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
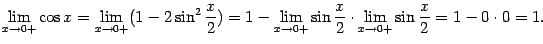
|
(2.4)
|
Тем
самым показано, что

Сделаем
теперь замену  ;
при этом база
перейдёт
в базу
;
при этом база
перейдёт
в базу 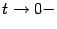 (что
означает, что если
(что
означает, что если  ,
то
,
то  ).
Значит,
).
Значит,

но 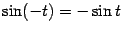 (
( --
нечётная функция), и поэтому
--
нечётная функция), и поэтому

Мы
показали, что левосторонний предел
также равен 1, что и завершает доказательство
теоремы.
Доказанная
теорема означает, что график
функции 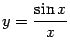 выглядит
так:
выглядит
так:
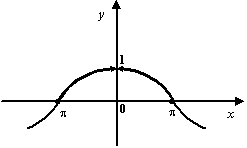
Рис.2.28.График
Приведём
примеры применения первого замечательного
предела для вычисления других родственных
пределов.
пределение 2.12 Вторым
замечательным пределом называется
предел

Число 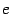 ,
заданное этим пределом, играет очень
большую роль как в математическом
анализе, так и в других разделах
математики. Число
часто
называют основанием
натуральных логарифмов.
,
заданное этим пределом, играет очень
большую роль как в математическом
анализе, так и в других разделах
математики. Число
часто
называют основанием
натуральных логарифмов.
Теорема 2.15 Второй
замечательный предел существует. Его
значение
--
число, лежащее между 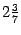 и
и  .
.
Более
подробное изучение числа
показывает,
что
--
иррациональное число, несколько первых
десятичных знаков которого таковы:

Для
доказательства теоремы
2.15 нам
понадобится следующая лемма; формула,
в ней полученная, называется формулой бинома
Ньютона.
Лемма 2.2 Пусть 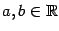 и
и 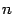 --
натуральное число. Тогда имеет место
формула
--
натуральное число. Тогда имеет место
формула
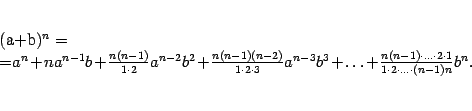
Заметим,
что в дроби
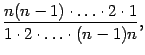
очевидно,
сокращаются все сомножители в числителе
и знаменателе, так что эта дробь равна
1. Аналогично, в предыдущем (не выписанном)
слагаемом после сокращения получается
коэффициент, равный
,
в третьем справа слагаемом -- равный 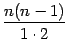 ,
и т. д. Таким образом, коэффициенты
в слагаемых, стоящих на одинаковых
местах, считая слева и справа от края
формулы, совпадают.
,
и т. д. Таким образом, коэффициенты
в слагаемых, стоящих на одинаковых
местах, считая слева и справа от края
формулы, совпадают.
11. Таблица эквивалентных
функций.
α(x)→0
1
|
sinα(x)~α(x)
|
2
|
arcsinα(x)~α(x)
|
3
|
tgα(x)~α(x)
|
4
|
arctgα(x)~α(x)
|
5
|
loga(1+α(x))~(logae)α(x)
|
6
|
ln(1+α(x))~α(x)
|
7
|
aα(x)-1~α(x)lna,a>0,a≠1
|
8
|
eα(x)-1~α(x)
|
9
|
(1+α(x))μ-1~μα(x)
|
10
|
1+α(x)n-1~α(x)n
|
11
|
1+α(x)-1~α(x)2
|
12
|
1-cosα(x)~12α2(x)
|
Если  то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.
то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.
например,
sinx~х при х→0, т.к 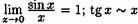 при
x→0, т. к.
при
x→0, т. к. 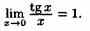
Теорема
18.1 .
Предел отношения двух бесконечно малых
функций не изменится, если каждую или
одну из них заменить эквивалентной ей
бесконечно малой.
Теорема
18.2 .
Разность двух эквивалентных бесконечно
малых функций есть бесконечно малая
более высокого порядка, чем каждая из
них.
12. Вычисление lim
U^V
(где х →
х◦).
13.Правило
Лопиталя
представляет
собой метод вычисления пределов, имеющих
неопределенность
типа 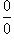 или
или 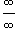 .
.
Пусть a является
некоторым конечным действительным
числом или равно бесконечности.
Правило
Лопиталя можно также применять к
неопределенностям типа  .
Первые две неопределенности
.
Первые две неопределенности  можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности
можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности 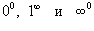 сводятся
к типу
сводятся
к типу  с
помощью соотношения
с
помощью соотношения
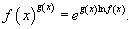
Правило
Лопиталя справедливо также и для
односторонних пределов.
Пример:
Вычислить
предел  .
.
Решение.
Дифференцируя
числитель и знаменатель, находим
значение предела:
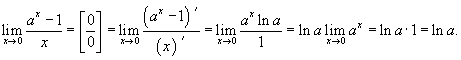
14. Непрерывность функции
в точке и на отрезке.
Рассмотрим
функцию 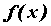 ,
определенную на некотором промежутке
,
определенную на некотором промежутке 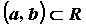 .
Функция
непрерывна
в точке
.
Функция
непрерывна
в точке 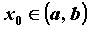 ,
если предел
функции в
точке
,
если предел
функции в
точке 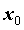 равен
значению функции в этой точке,
равен
значению функции в этой точке,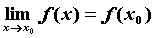 .
.
ПРИМЕР
1.
Доказательство непрерывности функции
в точке.
Свойства
функций, непрерывных на отрезке.
Функция,
непрерывная в каждой точке промежутка 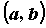 ,
называется непрерывной на промежутке.
Для функции, непрерывной на отрезке
,
называется непрерывной на промежутке.
Для функции, непрерывной на отрезке 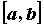 ,
справедливы следующие утверждения.
,
справедливы следующие утверждения.
Функция,
непрерывная на отрезке
,
достигает на нем своих наибольшего и
наименьшего значений, т.е. на
отрезке
существуют
точки  такие,
что
такие,
что
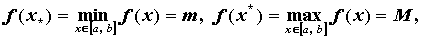
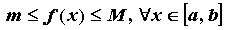 .
.
Если
функция 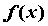 непрерывна
на отрезке
и
принимает на концах значения разных
знаков, то на интервале
непрерывна
на отрезке
и
принимает на концах значения разных
знаков, то на интервале  существует
точка
существует
точка 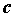 ,
в которой функция обращается в нуль,
т.е.
,
в которой функция обращается в нуль,
т.е. 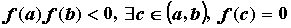 .
Это утверждение применяют для отделения
корней уравнений
.
Это утверждение применяют для отделения
корней уравнений 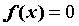 с
непрерывной левой частью — если найден
отрезок, на концах которого функция
принимает значения разных знаков, то
можно утверждать, что на этом отрезке
есть хотя бы один корень уравнения.
с
непрерывной левой частью — если найден
отрезок, на концах которого функция
принимает значения разных знаков, то
можно утверждать, что на этом отрезке
есть хотя бы один корень уравнения.
Если
функция
непрерывна
на отрезке
, дифференцируема хотя
бы на интервале 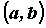 ,
то на интервале
существует
точка
,
такая, что
,
то на интервале
существует
точка
,
такая, что  .
Это свойство называют формулой Лагранжа
или формулой конечных приращений.
.
Это свойство называют формулой Лагранжа
или формулой конечных приращений.
15. Точки разрыва непрерывности функции, их типы.
Определение. Функции
f(x),  непрерывна
в точке
непрерывна
в точке  ,
если
,
если
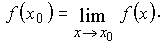
Графически
же непрерывность функции y = f(x)
означает непрерывность ее графика
как линии на плоскости Oxy.
Имеет
место следующая теорема (критерий
непрерывности).
Теорема. Функция
f(x),
непрерывна
в точке
тогда
и только тогда, когда
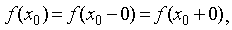
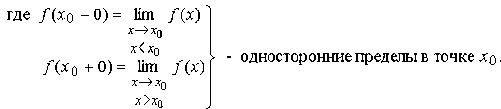
Как
видно из рис. 13, в точке x0 разрыва
функции f(x) ее левая "половина
графика" не соединяется с "правой
половиной", т.е. график "разорвался",
а поэтому f(x) в точке x0 имеет
разрыв.

Классификация
точек разрыва
Пусть
x0 -
точка разрыва функции f(x),
,
тогда имеют место следующие типы
разрывов.
1.
Устранимый разрыв первого рода:
если f(x0 -
x) = f(x0 +
x) ≠ f(x0)
либо f(x0 -
0) = f(x0 +
0) , а f(x0) не существует (рис. 14).
2.
Неустранимый разрыв первого рода:
если f(x0 -
0) ≠ f(x0 +
0) (рис. 15).
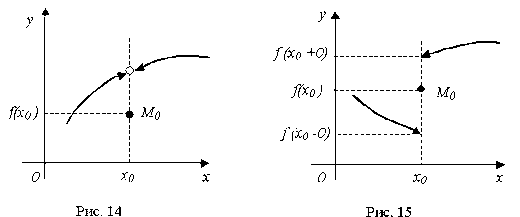
3.
Разрыв второго рода: если хотя бы
один из пределов f(x0 -
0) или f(x0 +
0) не существует или бесконечен
(рис. 16, 17, 18).

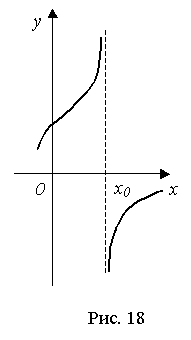
|
|
16. Применение пределов для
исследования функций.
Полная
схема исследования функции и построения
ее графика
План исследования
функции. Для
построения графика функции нужно:
1) найти область определения
и область значений функции,
2) установить, является
ли функция чётной или нечётной,
3) определить, является
ли функция периодической или нет,
4) найти нули
функции и её значения при x =
0,
5) найти интервалы
знакопостоянства,
6) найти интервалы
монотонности,
7) найти точки экстремума
и значения функции в этих точках,
8) проанализировать
поведение функции вблизи “особых”
точек
и при больших значениях модуля x .
1. Область
определения
2. Исследование
функции на четность, нечетность и
периодичность
Если
область определения функции симметрична
относительно нуля и для любого x из
области определения выполнено
равенство 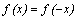 ,
то
,
то 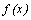 –
четная функция; если область определения
функции симметрична относительно нуля
и для любого x из
области определения выполнено
равенство
–
четная функция; если область определения
функции симметрична относительно нуля
и для любого x из
области определения выполнено
равенство 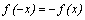 ,
то
–
нечетная функция; в противном случае,
,
то
–
нечетная функция; в противном случае,  –
общего вида. График четной функции
симметричен относительно оси ординат,
график нечетной функции симметричен
относительно начала координат.
–
общего вида. График четной функции
симметричен относительно оси ординат,
график нечетной функции симметричен
относительно начала координат.
3. Нахождение
точек пересечения графика функции с
осями координат
Точки
пересечения с осью ОХ:  ,
где
,
где  –
решение уравнения
–
решение уравнения  .
.
Точки
пересечения с осью ОY: 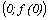 .
.
4. Нахождение
промежутков знакопостоянства функции
Промежутки
знакопостоянства функции – промежутки
из области определения функции, где
функция принимает положительные или
отрицательные значения, т.е.  или
или 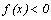 .
.
5. Нахождение
производной функции, области определения
производной, критических точек
Критические точки
функции – внутренние точки области
определения функции, в которых производная
не существует или равна нулю.
6. Нахождение
промежутков возрастания, убывания,
точек экстремума и экстремумов
Критические
точки функции разбивают область
определения функции на промежутки. Для
нахождения промежутков возрастания,
убывания и точек экстремума нужно
определить знак производной на каждом
из полученных промежутков. Если
производная функции положительна на
некотором промежутке I,
то функция возрастает на этом промежутке;
если производная функции отрицательна
на некотором промежутке I,
то функция убывает на этом промежутке.
Если при переходе через критическую
точку производная меняет знак, то данная
точка является точкой экстремума.
7. Нахождение
промежутков выпуклости функции и точек
перегиба
Для нахождения
промежутков выпуклости используется
вторая производная функции. Точки, в
которых вторая производная равна нулю
или не существует, разбивают область
определения функции на промежутки.
Если вторая производная на полученном
промежутке положительна, то график
функции имеет выпуклость вниз, если –
отрицательна, то график функции имеет
выпуклость вверх. Если при переходе
через точку, в которой вторая производная
равна нулю или не существует, вторая
производная меняет знак, то данная
точка является точкой перегиба.
8. Исследование
поведения функции на бесконечности и
в окрестности точек разрыва
Для
исследования поведения функции в
окрестности точки разрыва 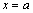 необходимо
вычислить односторонние пределы:
необходимо
вычислить односторонние пределы:  и
и 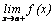 .
Если хотя бы один из данных пределов
равен бесконечности, то говорят, что
прямая
–
вертикальная асимптота.
.
Если хотя бы один из данных пределов
равен бесконечности, то говорят, что
прямая
–
вертикальная асимптота.
При
исследовании поведения функции на
бесконечности необходимо проверить,
не имеет ли график функции наклонных
асимптот при  и
и 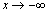 .
Для этого нужно вычислить следующие
пределы:
.
Для этого нужно вычислить следующие
пределы: 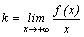 и
и 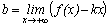 .
Если оба предела существуют, то
.
Если оба предела существуют, то 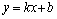 –
уравнение наклонной асимптоты при
–
уравнение наклонной асимптоты при  .
Частный случай наклонной асимптоты
при
.
Частный случай наклонной асимптоты
при  –
горизонтальная асимптота. Аналогично
ищется наклонная асимптота при
.
–
горизонтальная асимптота. Аналогично
ищется наклонная асимптота при
.
9. Построение
графика (при
необходимости нужно найти значения
функции в дополнительных точках)
Асимптоты
графика функции
Если
расстояние от точки, лежащей на кривой,
до некоторой прямой
стремится
к нулю при неограниченном удалении
этой точки от начала
координат,
то эта прямая называется асимптотой
кривой. Асимптоты
могут
быть вертикальными, горизонтальными
и наклонными.
Различают
вертикальные асимптоты и наклонные (в
частности, горизонтальные).
Если
у функции имеется бесконечный разрыв
при х=а, то прямая линия, параллельная
оси ОУ и проходящая через х=а, называется
вертикальной асимптотой. Пример: у=1/х,
здесь разрыв при х=0, и ось ОУ - вертикальная
асимптота. График функции приближается
к оси ОУ когда х приближается к
0.
Наклонные
асимптоты могут быть при х стремящемся
к бесконечности. Пример: у=1/х, при х
стремящемся к бесконечности, у стремится
к 0, и ось ОХ будет горизонтальной
асимптотой. Пример: у=2х+1-1/х, здесь х=0 -
вертикальная асимптота, а прямая у=2х-1
наклонная асимптота. Когда х уходит
далеко направо (или налево), график
функции приближается к прямой линии.
17. Производная функции в
точке.
Предел отношения
приращения функции к приращению
ее аргумента при
стремлении приращения аргумента к нулю,
если такой предел существует. Функцию,
имеющую конечную производную (в некоторой
точке), называют дифференцируемой (в
данной точке). Процесс вычисления
производной называется дифференци́рованием.
Обратный процесс —интегрирование.
18. Правила дифференцирование.
Если
функции f и g дифференцируемы
в точке 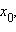 то
в этой же точке дифференцируемы сумма,
произведение и частное (если
то
в этой же точке дифференцируемы сумма,
произведение и частное (если  ) этих
функций, причем
) этих
функций, причем
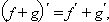
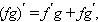
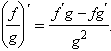
Доказательство
а) 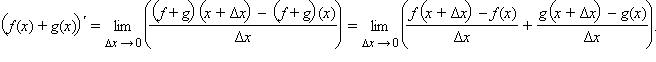 По
свойству предела суммы получаем
По
свойству предела суммы получаем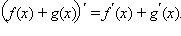
Постоянный
множитель C можно
выносить из-под знака производной:
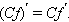
В
частности,
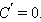
б)
Функцию f · g можно
записать в виде 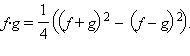 Но
Но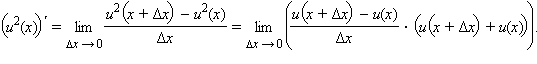 По
свойству предела произведения
получаем
По
свойству предела произведения
получаем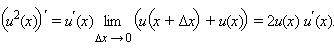 Используя
доказанное равенство, получим,
что
Используя
доказанное равенство, получим,
что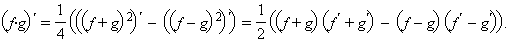 Раскрывая
скобки и приводя подобные члены, получим
формулу
Раскрывая
скобки и приводя подобные члены, получим
формулу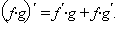
в)
Для доказательства этой формулы заметим,
что 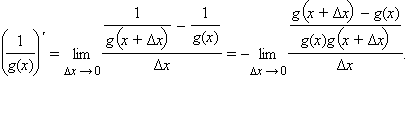 Воспользовавшись
свойством предела частного, получим
Воспользовавшись
свойством предела частного, получим 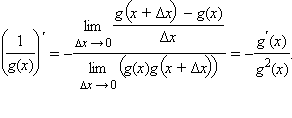 После
этого представим
После
этого представим 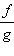 как
произведение функций f и
как
произведение функций f и 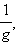 откуда
и следует доказываемая формула.
откуда
и следует доказываемая формула.
Если f дифференцируема,
то 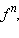 где
где 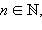 также
дифференцируема, причем
также
дифференцируема, причем
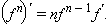
Доказательство
этой формулы предоставляем читателю.
Если
функция y = f ( x )
непрерывна и строго возрастает в
окрестности точки
причем 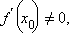 то
функция x = φ ( y ),
обратная к функции y = f (x ),
дифференцируема в точке y 0 = f ( x 0 ),
причем
то
функция x = φ ( y ),
обратная к функции y = f (x ),
дифференцируема в точке y 0 = f ( x 0 ),
причем
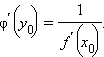
Если
функции y = f ( x )
и z = g ( y )
дифференцируемы в точках x 0 и y 0 = f ( x 0 )
соответственно, то сложная
функция z = g ( f ( x ))
дифференцируема в точке x 0,
причем
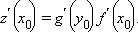
Следствием
этой теоремы является тот факт, что
дифференциал функции y = f ( x )
имеет один и тот же вид  как
в случае, когда x –
независимая переменная, так и в случае,
когда x –
дифференцируемая функция другого
переменного.
как
в случае, когда x –
независимая переменная, так и в случае,
когда x –
дифференцируемая функция другого
переменного.
Если f ( x )
– четная функция, то 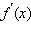 –
нечетная; если f ( x )
– нечетная функция, то
–
четная.
–
нечетная; если f ( x )
– нечетная функция, то
–
четная.
Пусть
в окрестности точки t 0 определены
функции x ( t )
и y ( t ),
причем x ( t )
непрерывна и строго монотонна. Пусть
в этой окрестности существуют
производные  и
и  Тогда
сложная функция y = y ( t ( x )),
где t ( x )
– функция, обратная x ( t ),
дифференцируема по x ,
причем
Тогда
сложная функция y = y ( t ( x )),
где t ( x )
– функция, обратная x ( t ),
дифференцируема по x ,
причем
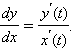
Таблица производных.
1.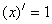
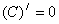
|
1.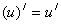
|
2.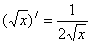
|
2.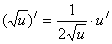
|
3.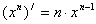
|
3.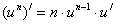
|
4.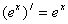
|
4.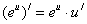
|
5.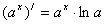
|
5.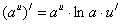
|
6.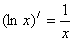
|
6.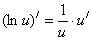
|
7.
|
7.
|
8.
|
8.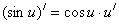
|
9.
|
9.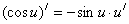
|
10. 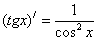
|
10. 
|
11. 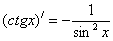
|
11. 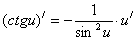
|
12. 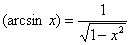
|
12. 
|
13. 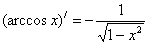
|
13. 
|
14. 
|
14. 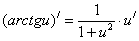
|
15. 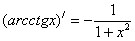
|
15. 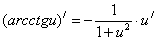
|
16.
|
16.
|
17.
|
17.
|
18.
|
18.
|
19.
|
19.
|
20.
|
20.
|
21.
|
21.
|
22.
|
22.
|
23.
|
23.
|
24.
|
24.
|
25.
|
25.
|
26.
|
26.
|
27.
|
27.
|
28.
|
28.
|
29.
|
29.
|
30.
|
30.
|
Преобразование производных уравнений.
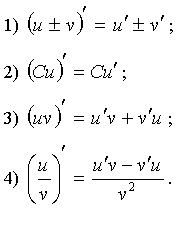
20.
Геометрический смысл производных.
Геометрический
смысл производной. Производная
в точке x 0 равна
угловому коэффициенту касательной к
графику функции y = f(x)
в этой точке.
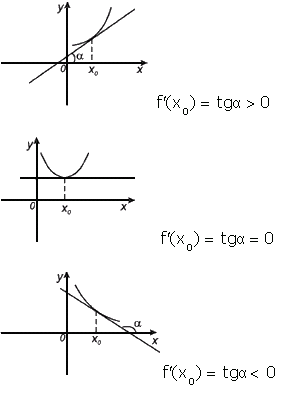
Рассмотрим
график функции y = f ( x ):
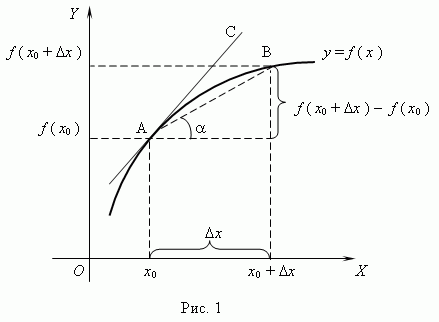
Из
рис.1 видно, что для любых двух
точек A и B графика
функции: 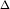 xf(x0+
x)−f(x0)=tg
xf(x0+
x)−f(x0)=tg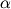 ,
где
,
где  -
угол наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей.
Если
зафиксировать точку A и
двигать по направлению к ней точку B,
то
-
угол наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей.
Если
зафиксировать точку A и
двигать по направлению к ней точку B,
то  x неограниченно
уменьшается и приближается к 0, а
секущая АВ приближается
к касательной АС.
Следовательно,
предел разностного отношения равен
угловому коэффициенту касательной в
точке A.
Отсюда
следует:производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке.
x неограниченно
уменьшается и приближается к 0, а
секущая АВ приближается
к касательной АС.
Следовательно,
предел разностного отношения равен
угловому коэффициенту касательной в
точке A.
Отсюда
следует:производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке.
21.
Производная сложной функции.
"Двухслойная" сложная функция
записывается в виде
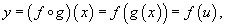
где u = g(x) - внутренняя функция,
являющаяся, в свою очередь, аргументом
для внешней функции f.
Если f и g -
дифференцируемые функции, то сложная
функция  также
дифференцируема по x и ее
производная равна
также
дифференцируема по x и ее
производная равна
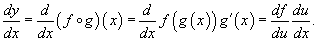
Данная
формула показывает, что производная
сложной функции равна произведению
производной внешней функции на
производную от внутренней функции.
Важно, однако, что производная
внутренней функции вычисляется в
точке x, а производная внешней
функции - в точке u = g(x)!
Эта
формула легко обобщается на случай,
когда сложная функция состоит из
нескольких "слоев", вложенных
иерархически друг в друга.
Рассмотрим
несколько примеров, иллюстрирующих
правило производной сложной функции.
Это правило широко применяется и во
многих других задачах раздела
"Дифференцирование".
|
Пример
1
|
|
Найти производную функции 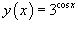 .
.
Решение.
Поскольку 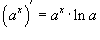 ,
то по правилу производной сложной
функции получаем
,
то по правилу производной сложной
функции получаем

|
22. Дифференцируемая функция.
Дифференциал
Пусть
функция 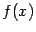 задана
в некоторой области
задана
в некоторой области 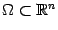 ,
и
,
и 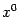 --
внутренняя точка этой области. Пусть
--
произвольная точка этой же области
--
внутренняя точка этой области. Пусть
--
произвольная точка этой же области  .
Разность
.
Разность 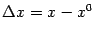 называется приращением
аргумента
;
называется приращением
аргумента
; 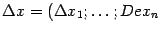 ,
где
,
где 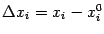 .
Разность значений функции
.
Разность значений функции 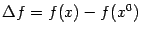 называется приращением,
или полным
приращением функции
называется приращением,
или полным
приращением функции 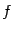 в
точке
,
соответствующим приращению
аргумента
в
точке
,
соответствующим приращению
аргумента 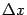 ;
; 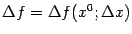 --
это функция от точки
и
приращения
.
--
это функция от точки
и
приращения
.
Предположим,
что приращение функции можно представить
в виде

|
(7.2)
|
где  --
некоторые числа. Подчеркнём, что эти
числа не зависят от
,
но могут измениться, если сменить
точку
.
Относительно величины
--
некоторые числа. Подчеркнём, что эти
числа не зависят от
,
но могут измениться, если сменить
точку
.
Относительно величины 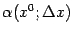 мы
предположим, что это функция, при
базе
мы
предположим, что это функция, при
базе 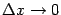 являющаяся
величиной большего порядка малости,
чем
являющаяся
величиной большего порядка малости,
чем 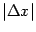 .
Это означает, если вспомнить определение
бесконечно малой величины большего
порядка малости относительно другой
бесконечно малой, что
.
Это означает, если вспомнить определение
бесконечно малой величины большего
порядка малости относительно другой
бесконечно малой, что

Заметим,
что сумма всех слагаемых левой части
(7.2),
кроме последнего, -- это линейная
функция от приращения аргумента
,
если точка
фиксирована.
Условие большей малости последнего
слагаемого (7.2)
относительно
означает,
что эта линейная функция -- главная
часть приращения функции.
Определение 7.11
Если указанное представление (7.2)
имеет место, то функцию
называют дифференцируемой
в точке
,
а линейную относительно
функцию

то есть главную линейную
часть приращения
функции, -- дифференциалом функции
в
точке
.
Если
функция
является
дифференцируемой в любой точке открытой
области
,
то функцию
называют дифференцируемой в
области
.
Таким
образом, приращение 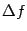 дифференцируемой
функции можно представить в виде суммы
дифференциала
дифференцируемой
функции можно представить в виде суммы
дифференциала 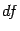 ,
то есть линейной части приращения, и
остатка
,
то есть линейной части приращения, и
остатка 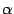 ,
который имеет более высокий порядок
малости, чем приращение
:
,
который имеет более высокий порядок
малости, чем приращение
:
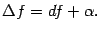
23.
Теорема о дифференцируемости функции
Теорема. Для
того, чтобы функция f(x)
была дифференцируемой в точке х,
необходимо и достаточно, чтобы она
имела производную в этой точке. При
этом 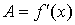 ,
,  и
и 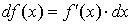 .
.
Геометрический
смысл дифференциала изображен на рис.
3.5. Заметьте, что производная
есть отношение дифференциала
функции к дифференциалу независимой
переменной:
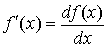 .
.
Это – самая
обычная дробь.

Рис. 3.5 Геометрический
смысл дифференциала.
24. Теоритический смысл
дифференциала
25.
Св-ва дифференциалов.
Выражение
производной через дифференциалы:
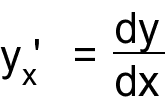 где
индекс "х" при y' показывает, что
производная берется по аргументу х. В
то же время дифференциалы dy и dx можно
брать по любому аргументу.
где
индекс "х" при y' показывает, что
производная берется по аргументу х. В
то же время дифференциалы dy и dx можно
брать по любому аргументу.
Выражение
дифференциала через производную:
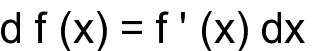 Используя
его, можно записать свойства дифференциалов,
используя свойства
производной.
Используя
его, можно записать свойства дифференциалов,
используя свойства
производной.
1.
Постоянный множитель можно вынести за
знак дифференциала:
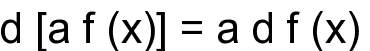
2.
дифференциал алгебраической суммы
функций равен алгебраической сумме
дифференциалов этих функций
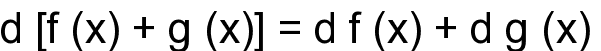
3.
дифференциал произведения
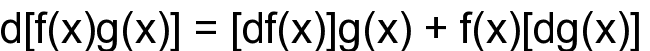
4.
дифференциал дроби (дифференциал
частного)
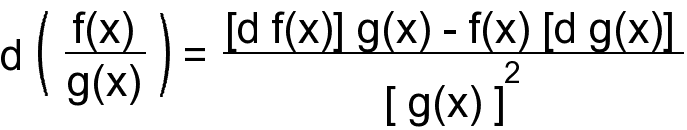
5.
дифференциал сложной функции
 где
d g(x), в свою очередь, можно дифференцировать
дальше.
где
d g(x), в свою очередь, можно дифференцировать
дальше.
26. Производные и дифференциалы
высших порядков.
Пусть
производная некоторой функции f дифференцируема.
Тогда производная от производной этой
функции называется второй
производной функции f и
обозначается f".
Таким образом,
f"(x)
= (f'(x))'.
Если
дифференцируема (n -
1)-я производная функции f,
то ее n-й
производной называется
производная от (n -
1)-й производной функции f и
обозначается f(n).
Итак,
f(n)(x)
= (f(n-1)(x))', n ϵ N, f(0)(x)
= f(x).
Число n называется порядком
производной.
Дифференциалом n-го
порядка функции f называется
дифференциал от дифференциала (n -
1)-го порядка этой же функции. Таким
образом,
dnf(x)
= d(dn-1f(x)), d0f(x)
= f(x), n ϵ N.
Если x -
независимая переменная, то
dx =
const и d2x = d3x =
... = dnx =
0.
В этом случае
справедлива формула
dnf(x)
= f(n)(x)(dx)n.
Производные n-го
порядка от основных элементарных
функций
Справедливы
формулы
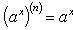

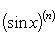



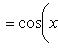

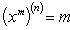


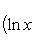
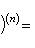
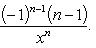
Формула Лейбница
Если u и v - n-кратно
дифференцируемые функции, то

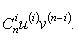
Производные n-го
порядка вектор-функции, комплекснозначной
и матричной функций
Если
компоненты 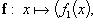
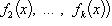 n-кратно
дифференцируемы, то
n-кратно
дифференцируемы, то 

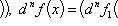

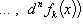 .
.
Аналогично
для комплекснозначной функции f и
матричной функции A имеем
формулы:
f(n)(x)
= u(n)(x)
+ iv(n)(x); dnf(x)
= dnu(x)
+ idnv(x);
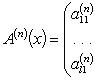
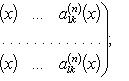
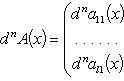
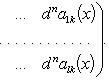
27. Применение производных
для исследования функций.
План исследования
функции. Для
построения графика функции нужно:
1) найти область определения
и область значений функции,
2) установить, является
ли функция чётной или нечётной,
3) определить, является
ли функция периодической или нет,
4) найти нули
функции и её значения при x =
0,
5) найти интервалы
знакопостоянства,
6) найти интервалы
монотонности,
7) найти точки экстремума
и значения функции в этих точках,
8) проанализировать
поведение функции вблизи “особых”
точек
и при больших значениях модуля x .
П
р и м е р . Исследуйте функцию f ( x )
= x 3 +
2x 2 x 2
и постройте график.
Р е ш е н и е . Исследуем функцию по
вышеприведенной схеме.
1) область определения x  R ( x –
любое действительное число);
R ( x –
любое действительное число);
область значений y
R,
так как f ( x )
– многочлен нечётной
степени;
2) функция f ( x )
не является ни чётной, ни нечётной
( поясните,
пожалуйста );
3) f ( x )
– непериодическая функция ( докажите
это сами );
4) график функции пересекается с
осью Y
в точке ( 0, – 2 ),
так как f (
0 ) = 2
; чтобы найти нули функции нужно
решить
уравнение: x 3 +
2x 2 x 2
= 0, один из корней
которого ( x =
1 ) очевиден. Другие корни находятся
( если
они есть! )
из решения квадратного уравнения:
x 2 +
3x +
2 = 0, которое получено делением многочлена
x 3 +
2x 2 x 2
на двучлен ( x –
1 ). Легко проверить,
что два других корня: x2 = 2
и x3
= 1.
Таким образом,
нулями функции
являются: 2, 1
и 1.
5) Это значит, что числовая ось делится
этими корнями на
четыре интервала знакопостоянства,
внутри которых
функция сохраняет свой знак :
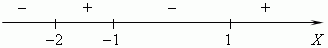
Этот результат может быть получен
разложением
многочлена
на множители:
x 3 +
2x 2 x 2
= ( x +
2 ) ( x +
1 ( x –
1 )
и оценкой знака произведения методом
интервалов
(
см. раздел «Неравенства» в главе
«Алгебра» ).
6)
Производная f’ ( x )
= 3x2 +
4x 1
не имеет точек, в которых
она не существует, поэтому её область
определения R (
все
действительные числа ); нули f’ ( x )
– это корни уравнения:
3x2 +
4x 1
= 0 .
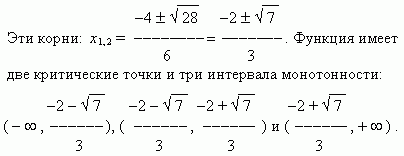
Полученные
результаты сведены в таблицу:
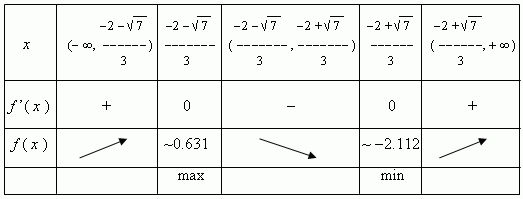




![]() при x → 0.
при x → 0.![]()

![]() в
точке a = 0 равен
0:
в
точке a = 0 равен
0: 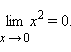 Предел
функции
в
точке a = 0 также
равен 0, хотя эта функция не существует
в этой точке (ее знаменатель обращается
в нуль). Предел функции
Предел
функции
в
точке a = 0 также
равен 0, хотя эта функция не существует
в этой точке (ее знаменатель обращается
в нуль). Предел функции  в
точке a = 0 равен
0, хотя значение функции в этой
точке f (0) = 1.
в
точке a = 0 равен
0, хотя значение функции в этой
точке f (0) = 1.![]() .
Предел отображения f по любому
интервалу
.
Предел отображения f по любому
интервалу ![]() наз.
пределом слева отображения f и обозначают
наз.
пределом слева отображения f и обозначают![]()
![]() ),
а предел по интервалу
),
а предел по интервалу ![]() наз.
пределом справа и обозначают
наз.
пределом справа и обозначают![]()
![]() ).
Если точка
).
Если точка ![]() является
предельной как слева, так и справа для
множества определения функции f, то
обычный предел
является
предельной как слева, так и справа для
множества определения функции f, то
обычный предел![]()
![]() и
и ![]()
![]() =А 0
(АєR), то α и ß называются бесконечно
малыми одного порядка.
=А 0
(АєR), то α и ß называются бесконечно
малыми одного порядка.![]()
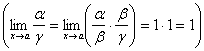
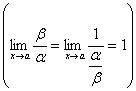
![]() ,
то и
,
то и ![]() или
или ![]() .
.![]()
![]()
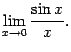
![]()

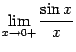 и
и 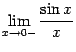 и
докажем, что каждый из них равен 1. Тогда
потеореме
2.1 двусторонний
предел
и
докажем, что каждый из них равен 1. Тогда
потеореме
2.1 двусторонний
предел 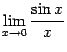 также
будет равняться 1.
также
будет равняться 1.![]() (этот
интервал -- одно из окончаний базы
(этот
интервал -- одно из окончаний базы ![]() ).
В тригонометрическом круге (радиуса
).
В тригонометрическом круге (радиуса ![]() )
с центром
)
с центром ![]() построим
центральный угол, равный
построим
центральный угол, равный ![]() ,
и проведём вертикальную касательную
в точке
,
и проведём вертикальную касательную
в точке ![]() пересечения
горизонтальной оси с окружностью (
пересечения
горизонтальной оси с окружностью (![]() ).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой
).
Обозначим точку пересечения луча с
углом наклона
с
окружностью буквой ![]() ,
а с вертикальной касательной --
буквой
,
а с вертикальной касательной --
буквой ![]() ;
через
;
через ![]() обозначим
проекцию точки
на
горизонтальную ось.
обозначим
проекцию точки
на
горизонтальную ось. 
![]() --
площадь треугольника
--
площадь треугольника ![]() ,
, ![]() --
площадь кругового сектора
,
а
--
площадь кругового сектора
,
а ![]() --
площадь треугольника
--
площадь треугольника ![]() .
Тогда очевидно следующее неравенство:
.
Тогда очевидно следующее неравенство:![]()
![]() ,
а вертикальная --
,
а вертикальная -- ![]() (это
высота треугольника
),
так что
(это
высота треугольника
),
так что 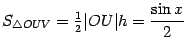 .
Площадь центрального сектора круга
радиуса
.
Площадь центрального сектора круга
радиуса ![]() с
центральным углом
равна
с
центральным углом
равна ![]() ,
так что
,
так что ![]() .
Из треугольника
находим,
что
.
Из треугольника
находим,
что ![]() .
Поэтому
.
Поэтому 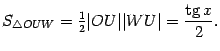 Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде
Неравенство,
связывающее площади трёх фигур, можно
теперь записать в виде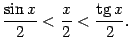

![]() )
так:
)
так: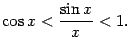
![]() в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части
в
левой части неравенства тоже равен 1,
то по теореме "о двух милиционерах"
предел средней части ![]() также
будет равен 1.
также
будет равен 1.![]() .
Сперва заметим, что
.
Сперва заметим, что ![]() ,
так как
равняется
длине дуги окружности
,
так как
равняется
длине дуги окружности ![]() ,
которая, очевидно, длиннее хорды
,
которая, очевидно, длиннее хорды ![]() .
Применяя теорему "о двух милиционерах"
к неравенству
.
Применяя теорему "о двух милиционерах"
к неравенству![]()
![]()
![]() показывает,
что и
показывает,
что и ![]() .
Теперь заметим, что
.
Теперь заметим, что ![]() .
Применяя теоремы о линейности предела
и о пределе произведения, получаем:
.
Применяя теоремы о линейности предела
и о пределе произведения, получаем:![]()

![]() ;
при этом база
перейдёт
в базу
;
при этом база
перейдёт
в базу ![]() (что
означает, что если
(что
означает, что если ![]() ,
то
,
то ![]() ).
Значит,
).
Значит,
![]() (
(![]() --
нечётная функция), и поэтому
--
нечётная функция), и поэтому
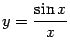 выглядит
так:
выглядит
так: 

![]() ,
заданное этим пределом, играет очень
большую роль как в математическом
анализе, так и в других разделах
математики. Число
часто
называют основанием
натуральных логарифмов.
,
заданное этим пределом, играет очень
большую роль как в математическом
анализе, так и в других разделах
математики. Число
часто
называют основанием
натуральных логарифмов.![]() и
и ![]() .
. ![]()
![]() и
и ![]() --
натуральное число. Тогда имеет место
формула
--
натуральное число. Тогда имеет место
формула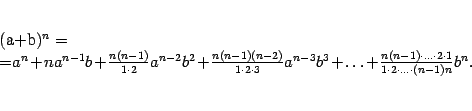
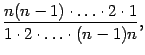
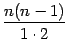 ,
и т. д. Таким образом, коэффициенты
в слагаемых, стоящих на одинаковых
местах, считая слева и справа от края
формулы, совпадают.
,
и т. д. Таким образом, коэффициенты
в слагаемых, стоящих на одинаковых
местах, считая слева и справа от края
формулы, совпадают.![]() то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.
то
α и ß называются эквивалентными
бесконечно малыми (при
х→x0);
это обозначается так: α~ß.![]() при
x→0, т. к.
при
x→0, т. к. ![]()
![]() или
или ![]() .
. ![]() и
и ![]() ,
то
,
то 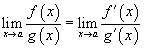 ;
;![]() и
и ![]() ,
то аналогично
.
,
то аналогично
.![]() .
Первые две неопределенности
.
Первые две неопределенности ![]() можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности
можно
свести к типу
или
с
помощью алгебраических преобразований.
А неопределенности ![]() сводятся
к типу
сводятся
к типу ![]() с
помощью соотношения
с
помощью соотношения![]()
 .
.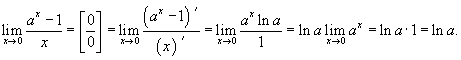
![]() ,
определенную на некотором промежутке
,
определенную на некотором промежутке ![]() .
Функция
непрерывна
в точке
.
Функция
непрерывна
в точке ![]() ,
если предел
функции в
точке
,
если предел
функции в
точке ![]() равен
значению функции в этой точке,
равен
значению функции в этой точке,![]() .
.![]() ,
называется непрерывной на промежутке.
Для функции, непрерывной на отрезке
,
называется непрерывной на промежутке.
Для функции, непрерывной на отрезке ![]() ,
справедливы следующие утверждения.
,
справедливы следующие утверждения.![]() такие,
что
такие,
что![]()
![]() .
.![]() непрерывна
на отрезке
и
принимает на концах значения разных
знаков, то на интервале
непрерывна
на отрезке
и
принимает на концах значения разных
знаков, то на интервале ![]() существует
точка
существует
точка ![]() ,
в которой функция обращается в нуль,
т.е.
,
в которой функция обращается в нуль,
т.е. ![]() .
Это утверждение применяют для отделения
корней уравнений
.
Это утверждение применяют для отделения
корней уравнений ![]() с
непрерывной левой частью — если найден
отрезок, на концах которого функция
принимает значения разных знаков, то
можно утверждать, что на этом отрезке
есть хотя бы один корень уравнения.
с
непрерывной левой частью — если найден
отрезок, на концах которого функция
принимает значения разных знаков, то
можно утверждать, что на этом отрезке
есть хотя бы один корень уравнения.![]() ,
то на интервале
существует
точка
,
такая, что
,
то на интервале
существует
точка
,
такая, что ![]() .
Это свойство называют формулой Лагранжа
или формулой конечных приращений.
.
Это свойство называют формулой Лагранжа
или формулой конечных приращений.![]() непрерывна
в точке
непрерывна
в точке ![]() ,
если
,
если![]()
![]()
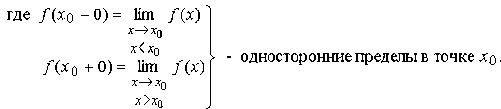

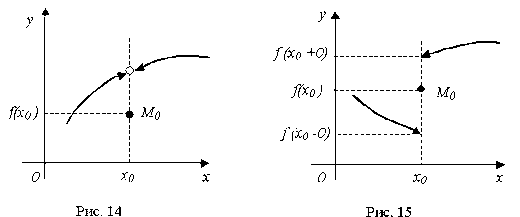

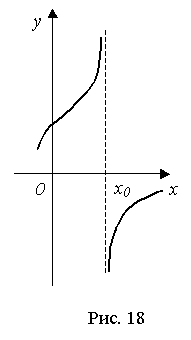
![]() ,
то
,
то ![]() –
четная функция; если область определения
функции симметрична относительно нуля
и для любого x из
области определения выполнено
равенство
–
четная функция; если область определения
функции симметрична относительно нуля
и для любого x из
области определения выполнено
равенство ![]() ,
то
–
нечетная функция; в противном случае,
,
то
–
нечетная функция; в противном случае, ![]() –
общего вида. График четной функции
симметричен относительно оси ординат,
график нечетной функции симметричен
относительно начала координат.
–
общего вида. График четной функции
симметричен относительно оси ординат,
график нечетной функции симметричен
относительно начала координат.![]() ,
где
,
где ![]() –
решение уравнения
–
решение уравнения ![]() .
.![]() .
.![]() или
или ![]() .
.![]() необходимо
вычислить односторонние пределы:
необходимо
вычислить односторонние пределы: ![]() и
и ![]() .
Если хотя бы один из данных пределов
равен бесконечности, то говорят, что
прямая
–
вертикальная асимптота.
.
Если хотя бы один из данных пределов
равен бесконечности, то говорят, что
прямая
–
вертикальная асимптота.![]() и
и ![]() .
Для этого нужно вычислить следующие
пределы:
.
Для этого нужно вычислить следующие
пределы: ![]() и
и ![]() .
Если оба предела существуют, то
.
Если оба предела существуют, то ![]() –
уравнение наклонной асимптоты при
–
уравнение наклонной асимптоты при ![]() .
Частный случай наклонной асимптоты
при
.
Частный случай наклонной асимптоты
при ![]() –
горизонтальная асимптота. Аналогично
ищется наклонная асимптота при
.
–
горизонтальная асимптота. Аналогично
ищется наклонная асимптота при
. ![]() то
в этой же точке дифференцируемы сумма,
произведение и частное (если
то
в этой же точке дифференцируемы сумма,
произведение и частное (если ![]() ) этих
функций, причем
) этих
функций, причем![]()
![]()
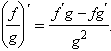
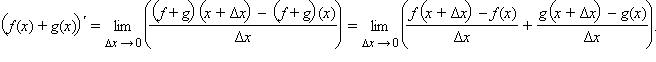 По
свойству предела суммы получаем
По
свойству предела суммы получаем![]()
![]()
![]()
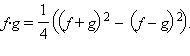 Но
Но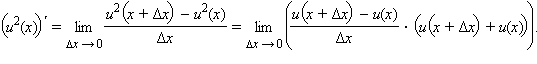 По
свойству предела произведения
получаем
По
свойству предела произведения
получаем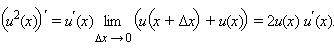 Используя
доказанное равенство, получим,
что
Используя
доказанное равенство, получим,
что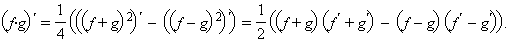 Раскрывая
скобки и приводя подобные члены, получим
формулу
Раскрывая
скобки и приводя подобные члены, получим
формулу![]()
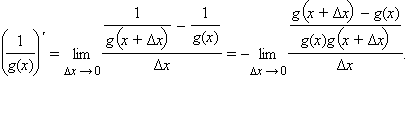 Воспользовавшись
свойством предела частного, получим
Воспользовавшись
свойством предела частного, получим 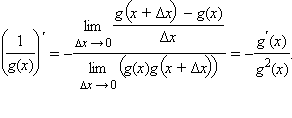 После
этого представим
После
этого представим ![]() как
произведение функций f и
как
произведение функций f и ![]() откуда
и следует доказываемая формула.
откуда
и следует доказываемая формула.![]() где
где ![]() также
дифференцируема, причем
также
дифференцируема, причем
![]()
![]() то
функция x = φ ( y ),
обратная к функции y = f (x ),
дифференцируема в точке y 0 = f ( x 0 ),
причем
то
функция x = φ ( y ),
обратная к функции y = f (x ),
дифференцируема в точке y 0 = f ( x 0 ),
причем
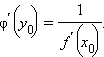
![]()
![]() как
в случае, когда x –
независимая переменная, так и в случае,
когда x –
дифференцируемая функция другого
переменного.
как
в случае, когда x –
независимая переменная, так и в случае,
когда x –
дифференцируемая функция другого
переменного.![]() –
нечетная; если f ( x )
– нечетная функция, то
–
четная.
–
нечетная; если f ( x )
– нечетная функция, то
–
четная.![]() и
и ![]() Тогда
сложная функция y = y ( t ( x )),
где t ( x )
– функция, обратная x ( t ),
дифференцируема по x ,
причем
Тогда
сложная функция y = y ( t ( x )),
где t ( x )
– функция, обратная x ( t ),
дифференцируема по x ,
причем
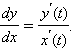
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
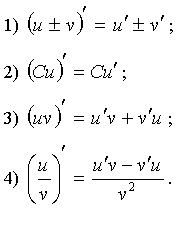
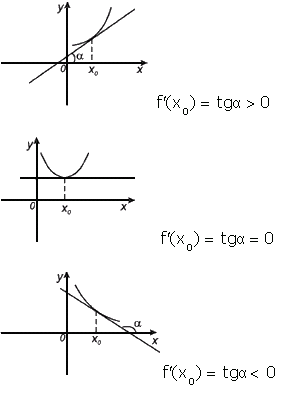
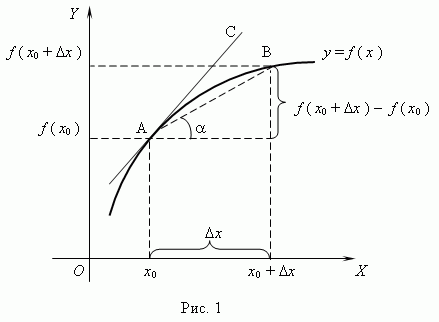
![]() xf(x0+
x)−f(x0)=tg
xf(x0+
x)−f(x0)=tg![]() ,
где
,
где ![]() -
угол наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей.
Если
зафиксировать точку A и
двигать по направлению к ней точку B,
то
-
угол наклона секущей AB.
Таким
образом, разностное отношение равно
угловому коэффициенту секущей.
Если
зафиксировать точку A и
двигать по направлению к ней точку B,
то ![]() x неограниченно
уменьшается и приближается к 0, а
секущая АВ приближается
к касательной АС.
Следовательно,
предел разностного отношения равен
угловому коэффициенту касательной в
точке A.
Отсюда
следует:производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке.
x неограниченно
уменьшается и приближается к 0, а
секущая АВ приближается
к касательной АС.
Следовательно,
предел разностного отношения равен
угловому коэффициенту касательной в
точке A.
Отсюда
следует:производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке.![]()
![]() также
дифференцируема по x и ее
производная равна
также
дифференцируема по x и ее
производная равна![]()
![]() .
.![]() ,
то по правилу производной сложной
функции получаем
,
то по правилу производной сложной
функции получаем![]()
![]() задана
в некоторой области
задана
в некоторой области ![]() ,
и
,
и ![]() --
внутренняя точка этой области. Пусть
--
произвольная точка этой же области
--
внутренняя точка этой области. Пусть
--
произвольная точка этой же области ![]() .
Разность
.
Разность ![]() называется приращением
аргумента
;
называется приращением
аргумента
; ![]() ,
где
,
где ![]() .
Разность значений функции
.
Разность значений функции ![]() называется приращением,
или полным
приращением функции
называется приращением,
или полным
приращением функции ![]() в
точке
,
соответствующим приращению
аргумента
в
точке
,
соответствующим приращению
аргумента ![]() ;
; ![]() --
это функция от точки
и
приращения
.
--
это функция от точки
и
приращения
.![]()
![]() --
некоторые числа. Подчеркнём, что эти
числа не зависят от
,
но могут измениться, если сменить
точку
.
Относительно величины
--
некоторые числа. Подчеркнём, что эти
числа не зависят от
,
но могут измениться, если сменить
точку
.
Относительно величины ![]() мы
предположим, что это функция, при
базе
мы
предположим, что это функция, при
базе ![]() являющаяся
величиной большего порядка малости,
чем
являющаяся
величиной большего порядка малости,
чем ![]() .
Это означает, если вспомнить определение
бесконечно малой величины большего
порядка малости относительно другой
бесконечно малой, что
.
Это означает, если вспомнить определение
бесконечно малой величины большего
порядка малости относительно другой
бесконечно малой, что
![]()
![]() дифференцируемой
функции можно представить в виде суммы
дифференциала
дифференцируемой
функции можно представить в виде суммы
дифференциала ![]() ,
то есть линейной части приращения, и
остатка
,
то есть линейной части приращения, и
остатка ![]() ,
который имеет более высокий порядок
малости, чем приращение
:
,
который имеет более высокий порядок
малости, чем приращение
:![]()
![]() ,
, ![]() и
и ![]() .
.![]() .
.
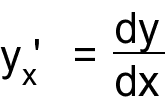 где
индекс "х" при y' показывает, что
производная берется по аргументу х. В
то же время дифференциалы dy и dx можно
брать по любому аргументу.
где
индекс "х" при y' показывает, что
производная берется по аргументу х. В
то же время дифференциалы dy и dx можно
брать по любому аргументу.![]() Используя
его, можно записать свойства дифференциалов,
используя свойства
производной.
Используя
его, можно записать свойства дифференциалов,
используя свойства
производной.![]()
![]()
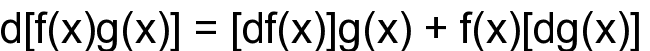
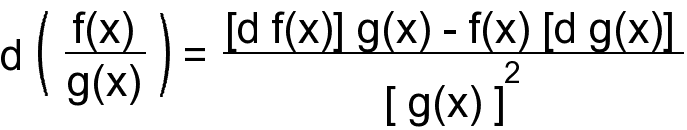
 где
d g(x), в свою очередь, можно дифференцировать
дальше.
где
d g(x), в свою очередь, можно дифференцировать
дальше.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]() n-кратно
дифференцируемы, то
n-кратно
дифференцируемы, то ![]()
![]()
![]()
![]()
![]() .
.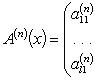
![]() R ( x –
любое действительное число);
R ( x –
любое действительное число);![]()