43 Понятие о коэффициентах ошибок

Пусть входной сигнал v(t) меняется настолько медленно, что на текущем интервале времени, соизмеримом с длительностью ПП в системе (речь идет о практической длительности переходного процесса t_р), он может быть с достаточной степенью точности представлен в виде полинома степени r где a_i=v⁽ⁱ⁾(t) – i-ая производная сигнала v(t).

Е сли известна весовая ф-я замкнутой системы k(t), то значение выходного сигнала определяется интегралом свертки Если момент приложения входного сигнала достаточно удален от текущего момента времени, т.е. t₀= - ∞, то в системе к интересующему нас моменту t≥0 ПП уже наверняка закончится, так что будет иметь место установившийся процесс, который определяется выражением , отсюда .Вводя обозначение получаем другое выражение для выходной величины . Величины , н-ся моментами весовой ф-ии. При этом установившаяся ошибка . Обозн. ,получаем ₍₂₇₎Входящие в выражение коэффициенты C_i получили название коэффициентов ошибок.

Коэффициенты ошибок статических и астатических систем.

Первые три коэффициента ошибок С₀, С₁, С₂ имеют специальные названия, соответствующие их физическому смыслу. Коэффициент С₀ называется коэффициентом статической ошибки ε_ст или коэффициентом ошибки по положению, так как он определяет величину установившейся ошибки при постоянном входном сигнале. Действительно, если v(t)=a₀=const, то согласно (27) ε_уст= ε_ст=С₀а₀. Последняя формула позволяет дать другое определение для статических и астатических систем.

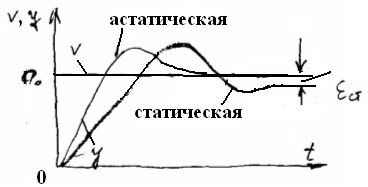Системы, для к. ε_ст≠0, по введенному выше определению, н-ся статическими системами. Однако ε_ст ≠ 0 только тогда, когда С₀ ≠ 0. След-но, неравенство нулю коэфф. ошибки С₀ явл. признаком статической системы. В астатических системах статическая ошибка равна нулю. Поэтому условие С₀=0 обеспечивает системе автоматического управления астатизм первого порядка.

Коэффициент С₁ называется коэффициентом ошибки по скорости, так как от него зависит величина ошибки по скорости ε_ск. Если С₀=0, а С₁ ≠ 0, то система имеет постоянную ошибку по скорости при входном сигнале, меняющемся с постоянной скоростью ( ). Действительно, когда v(t)=a₁t, то (t)=a₁, (t)=0 и согласно (27) ε_уст= ε_ск=С₁а₁. Если С₀=С₁=0, то ε_ск=0, т.е. система имеет астатизм 2го порядка ( ). Такая система, как известно, отрабатывает входной сигнал, меняющийся с постоянной скоростью, без ошибки. Наконец, величина С₂ н-ся коэфф. ошибки по ускорению, так как от нее зависит величина ошибки по ускорению. Если С₀=С₁=0, а С₂ ≠ 0, то система отрабатывает с постоянной ошибкой сигнал, меняющийся с постоянным ускорением а₂. Действительно, когда v(t)= a₂t², то (t)=a₂t, (t)=a₂, (t)=0, так что ε_уст= ε_уск=С₂а₂=const. Если С₀=С₁=С₂=0, то ε_уск=0, т.е. система имеет астатизм третьего порядка. Такая система отрабатывает без ошибки входной сигнал, меняющийся с постоянным ускорением.

Как видим, число первых нулевых коэффициентов ошибок определяет порядок астатизма системы.

44.(Вкл в себя72) Количественная оценка неопределенностей модели объекта

Введем следующие обозначения: П- множество всех возмущенных объектов («множество неопределенности»), W₁ (p) - передаточная функция номинальной модели ОУ (невозмущенного объекта), которое также входит во множество П, W_1р (p) П– передаточная функция реальной (возмущенной) модели ОУ, одного из элементов множества П.

Классификация неопределенности.

Параметрическая неопределенность. Здесь структура модели объекта известна (включая порядок (степень)), но некоторые параметры являются неопределенными. Такой вид неопределенности называют также структурированной неопределенностью. Это самый наглядный вид неопределенности. Например, пусть ПФ объекта W_1p(p)=k₁/(p+a) с параметрами

k₁=1.0 0.2, a=10 1.3. Выберем номинальную ПФ W₁(p)=1.0 /(p+10).

При этом все возможные модели объекта W_1р (p) П, где

П={k₁/(p+a): 0.8 k₁ 1.2, 8.7 a 11.3}.

Параметрические модели редко используются, т.к. они не оставляют места для немоделируемой динамики (см. ниже), и приводят к достаточно сложным методам анализа и синтеза систем.

Неопределенность игнорируемой или немоделируемой динамики. Здесь ошибка модели имеет место из-за неучтенной динамики (обычно в высокочастотной области) или из-за преднамеренного игнорирования динамики (с целью получить простую модель) или из-за недостаточного понимания сути физических процессов. Любая модель реального объекта будет содержать эти источники неопределенности. Такой вид неопределенности называют также неструктурированной неопределенностью. Сосредоточенная (взятая в целом) неопределенность. Здесь описание неопределенности представляет один или несколько источников параметрической неопределенности и/или немоделируемой динамики, объединенных (комбинируемых) в одну сосредоточенную неопределенность. Рассмотрим в качестве сосредоточенной неопределенности мультипликативную неопределенность, при которой (рис. 1)

П: , (1)

где - произвольная передаточная функция, удовлетворяющая условию , и - передаточная функция, определяющая границы неопределенности. Индекс относится к норме, которая, как известно, называется бесконечной нормой и обозначается . Она определяет

.

П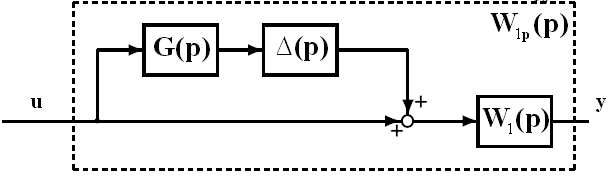 ричина для использования нормы в том, что при другой форме записи

Рис. 1

у словия можно опустить . Здесь произвольная устойчивая ПФ (все полюсы левые), модуль, другими словами, АЧХ которой на любой частоте меньше или равна 1.

Некоторые допустимые ПФ для : .

Представление неопределенности в частотной (комплексной) области.

Лучший путь представить мультипликативную неопределенность в частотной области. Рассмотрим, как это можно сделать на примере. Пусть дана ПФ объекта

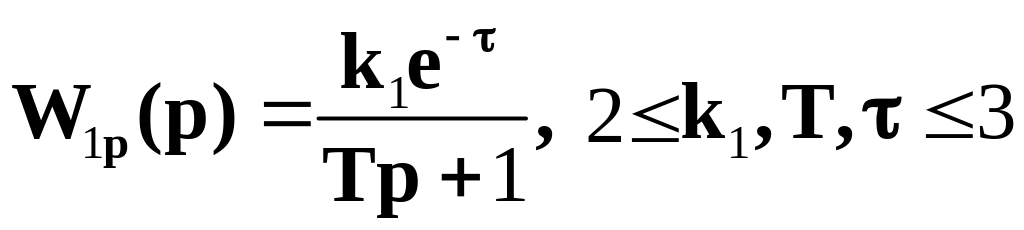
с параметрическими неопределенностями. Изменяя параметры в заданных пределах для серии значений частоты на плоскости АФХ , мы получим множество точек , соответствующих различным (сочетаниям) наборам параметров из области определения, и найдем границы районов неопределенности для каждого множества точек (рис. 2).

Рис. 2

З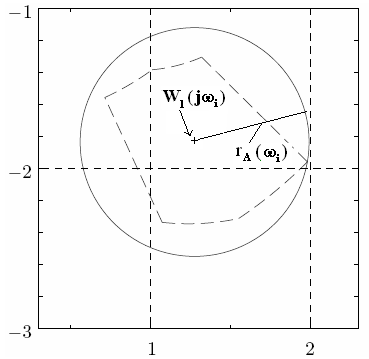 атем для каждого значения (рис. 3) выбираем точку, соответствующую «типичному» значению (на рис. обозначена +), которое принимаем за номинальное значение множества П, после чего находим радиус r_A( ) окружности с центром в точке , которая охватывает с максимальной близостью район неопределенности, и принимаем за границу мультипликативной неопределенности r_M( )= r_A( )/| |.

Рис. 3

На рис. 3 показана аппроксимация с помощью окружности (сплошная линия) исходного района неопределенности (пунктирная линия). Кривые соответствуют частоте = 0.2 на рис. 2. Здесь r_M( ) есть максимальная граница мультипликативной неопределенности.

Альтернативно можно ввести понятие аддитивной неопределенности, описываемой множеством

П: , (2) где произвольная устойчивая ПФ

,

- граница аддитивной неопределенности. Аддитивная неопределенность может также быть представлена с помощью окружностей (рис. 4), т.е. r_A( ), причем радиус r_A( ) каждой окружности определяет максимальную границу аддитивной неопределенности для каждого значения частоты.

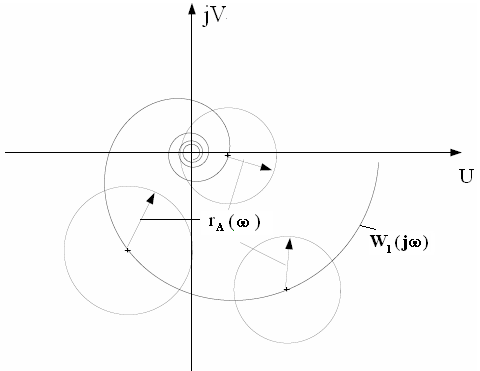
Рис. 4

Мультипликативная неопределенность (1) эквивалентна аддитивной неопределенности (2) при

= / . (3)

Алгоритм определения границ для неопределенностей:

Выбираем номинальную модель .

Аддитивная неопределенность. На каждой частоте находим наименьший радиус r_A( )окружности, которая охватывает все возможные модели, принадлежащие множеству П, и определяем границу

r_A( )= . (4) Мультипликативная неопределенность. Определяется

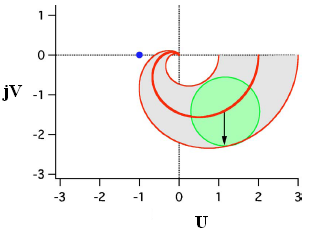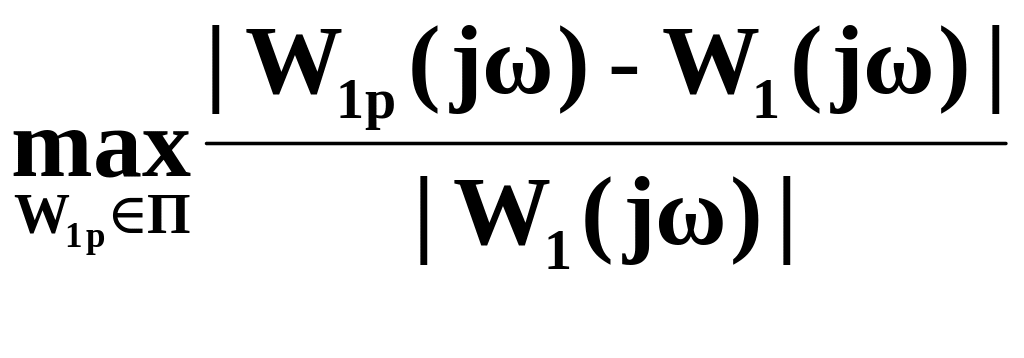к ак r_M( )= . (5)

Суперпозиция (наложение) кругов с радиусом r_A( ) для 0 формирует затененную полосу и АФХ номинального ОУ (сплошная линия) (рис. 5). Тонкие линии, определяющие затененную полосу, говорят о том, что АФХ реального объекта проходит где-нибудь внутри затененной полосы.

З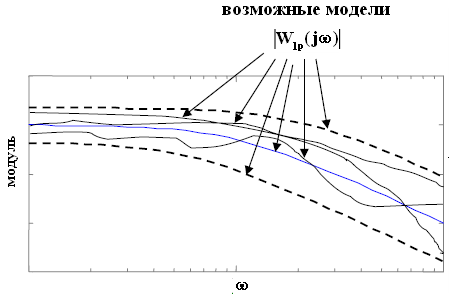 атененную полосу можно отобразить также с помощью АЧХ

Рис. 6 На этом рисунке границы затененной полосы + и − изображены пунктирными линиями, АЧХ номинальной модели объекта синей

линией, АЧХ возможных моделей объекта сплошными черными линиями.