
- •2.1 Степенная последовательность графа. Лемма о рукопожатиях. Критерий графичности последовательности.
- •По индукции Формулу включений-исключений можно доказать по индукции.ТПри формула включений-исключений тривиальна: Пусть формула верна для , докажем ее для .
- •Комбинаторное доказательство Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений[4].
- •2. Число всех беспорядков на множестве {1,2,…,n} равно
- •Биномиальная формула (бином Ньютона)
- •11.2) Число всех отображений, число сюръективных отображений конечных множеств (элементы в неразличимы).
- •1 2.2) Биномиальная формула.
- •16.1.) Теорема. Карта g является k-раскрашиваемой тогда и только тогда, когда геометрически двойственный граф g* вершинно k-раскрашиваем.
По индукции Формулу включений-исключений можно доказать по индукции.ТПри формула включений-исключений тривиальна: Пусть формула верна для , докажем ее для .
Пусть
каждый элемент множества
может
обладать или не обладать любым из
свойств ![]() .
Применим формулу включений-исключений
для свойств
.
Применим формулу включений-исключений
для свойств ![]() :
:
![]()
Теперь
применим формулу для свойств
к
множеству ![]() объектов,
для которых выполнено свойство
объектов,
для которых выполнено свойство ![]() :
:
![]()
Наконец,
применим формулу для одного свойства
к
совокупности ![]() ,
объектов, которые не обладают свойствами
,
объектов, которые не обладают свойствами ![]() :
:
![]()
Комбинируя
выписанные три формулы, получим формулу
включений-исключений для ![]() свойств
свойств ![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Комбинаторное доказательство Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений[4].
Если
элемент ![]() не
обладает ни одним из свойств
,
то в правой части формулы он учитывается
ровно 1 раз (в члене
).
не
обладает ни одним из свойств
,
то в правой части формулы он учитывается
ровно 1 раз (в члене
).
Пусть
элемент
обладает в
точности ![]() свойствами,
скажем
свойствами,
скажем ![]() .
Он дает по 1 в тех слагаемых суммы
.
Он дает по 1 в тех слагаемых суммы ![]() ,
для которых
,
для которых ![]() есть
подмножество
есть
подмножество ![]() ,
и 0 для остальных. Число таких подмножеств
по определению есть число
сочетаний
,
и 0 для остальных. Число таких подмножеств
по определению есть число
сочетаний ![]() .
Следовательно, вклад элемента
в
правую часть равен
.
Следовательно, вклад элемента
в
правую часть равен
![]()
При ![]() числа
сочетаний равны нулю. Оставшаяся сумма
в силу биномиальной
теоремы равна
числа
сочетаний равны нулю. Оставшаяся сумма
в силу биномиальной
теоремы равна![]()
Таким
образом, правая часть формулы
включений-исключений учитывает каждый
элемент, не имеющий указанных свойств
точно по одному разу, а каждый элемент,
обладающий хотя бы одним из свойств —
нуль раз. Следовательно, она равна
количеству элементов, не обладающих ни
одним из свойств
,
то есть ![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Билет 5. 1. Деревья. Характеризация дерева. Деревья Деревья открывались независимо несколько раз. Еще в позапрошлом веке Г. Кирхгоф ввел деревья и применил их к исследованию электрических цепей, а А. Кэли. перечисляя изомеры насыщенных углеводородов, еще раз открыл деревья и первым исследовал их свойства. Тогда же деревья были введены и исследованы К. Жорданом как чисто математический объект. Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или лесам). Таким образом, компонентами леса являются деревья. На рис. 10.1 изображены все деревья с шестью вершинами.
Рис. 9.1 - Су шествует несколько вариантов определения дерева; некоторые из них отражены в следующей теореме.
Теорема Для (я, т)~графа G следующие утверждения эквивалентны: 1) G - - дерево; 2) G связный граф u т ~~ п - 1: 3) G ациклический граф и т - я - 1; 4) любые две несовпадающие вершины графа G соединяет единственная простая цепь; 5) (j ациклический граф, обладающий тем свойством, что если, какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл..
♦ 1) => 2) Воспользуемся индукцией по п. При п = 1 утверждение тривиально. Пусть п > I. е е EG. В дереве G нет циклов, следовательно, согласно утверждению 4.5. граф G е имеет ровно две компоненты 1) и 7:, каждая из которых есть дерево. Пусть дерево 1) является (я,-, ш,)-графом, i= 1, 2. По индуктивному предположению верно равенство
т, = щ - I (1) Далее имеем т = /и; + т2 + 1 = (я/ - 1) + (Пз - 1) ■+ 1 = (я/ + щ) - 1 = я - I.
2J ==> 3) Граф G связен и т = п - 1. Нужно доказать, что в G нет циклов. Пусть, напротив, в графе G есть цикл и пусть е — ребро этого цикла. Тогда граф G - е связен (по утверждению 4.5) и имеет и - 2 ребра, что противоречит теореме 4.6. Следовательно, G — ациклический граф.
3) =-> 4) Пусть к — число компонент графа G. Пусть, далее, компонента У) является (я,. ш,)-графом. Так как Т, — дерево, то верно равенство (I). Теперь имеем п — 1 = m - m} + пи +...+ пц- = {щ -1) + (иг - 1) +...+ (щ -1) = (я/ + п2 + ... + л*) ~ к= п -к, т. в. к = I. Итак. G — связный граф и потому любые несовпадающие вершины и и V соединены в нем простой цепью. Если бы в G были две несовпадающие простые (и, р)-цепи, то согласно утверждению 4.1 в их объединение содержало бы цикл. Следовательно, каждые две вершины соединены единственной простой цепью.
4) и> 5) Пара несовпадающих вершин, принадлежащих одному циклу, соединена по меньшей мере двумя простыми цепями. Следовательно, граф G ациклический. Пусть и и v — две его несмежные вершины. Присоединим к графу G ребро е = uv. В G есть простая (и. г)-цепь. которая в G + е дополняется до цикла. В силу утверждения 4.1 г этот цикл единственный (иначе в G после выбрасывания е из G + е оставался бы цикл).
5) ==> I) Нужно доказать, что граф G связен. Если бы вершины и и v принадлежали разным компонентам графа G, то граф G + uv не имел бы циклов, что противоречит утверждению 5 теоремы. Итак, G связен и потому является деревом. ♦
Следствие В любом дереве порядка я > 2 имеется не менее двух концевых вершин.
♦ Пусть (//. dj. .... d„ — степенная последовательность дерева. Тогда di + d2 +... + d„ = 2п - 2 (лемма о рукопожатиях) и все dj > 0. Следовательно, хотя бы два числа из последовательности степеней вершин равны 1. ♦
2. Остов наименьшего веса. Алгоритм Краскала. Пусть G — граф. и1: EG —> R — вещественнозначная функция, ставящая в соответствие каждому ребру е положительное (или неотрицательное) число w(e) — вес ребра е. Пару (G, и) назовем взвешенным графом. Под длиной (или весом) любого подграфа взвешенного графа будем понимать сумму весов его ребер.
Рассмотрим следующую задачу: по взвешенном связном графе требуется найти остов минимального веса, эта задача возникает при проектировании линий электропередачи, трубопроводов, дорог и т. п., когда требуется заданные центры соединить некоторой системой каналов связи так, чтобы любые два центра были связаны либо непосредственно соединяющим их каналом, либо через другие центры и каналы, и чтобы общая длина (или, например, стоимость) каналов связи была минимальной, В этой ситуации заданные центры можно считать вершинами полного графа с весами ребер, равными длинам (стоимости) соединяющих эти центры каналов. Тогда искомая сеть будет кратчайшим остовным подграфом полного графа. Очевидно, что этот кратчайший остовный подграф должен быть деревом. Поскольку полный граф К„ содержит п" " различных остовных деревьев, то решение этой задачи «слепым» перебором вариантов потребовало бы чрезвычайно больших вычислений даже при относительно малых П . Однако для ее решения имеются эффективные алгоритмы. Опишем два из них —- алгоритмы Дж. Краскала (1956 г.) и Р. Прима (1957 г.), применимые к произвольному связному графу.
Задача об остове минимального веса (о кратчайшем остове): в связном взвешенном графе ((;, w) порядка п найти остов минимального веса. Алгоритм Краскала: 1.Строим граф T1 = On+e1, присоединяя к пустому граф на множестве веришн VG ребро e1 принадлежащей EG минимального вес. 2.Если граф T1 уже построен и I < n-1, то строим граф Ti+1= T1+ei+1, где ei+1 – ребро графа G имеющее минимальный вес среди ребер не входящих в Т1 и не составляющих циклов с ребрами из Т1 3.Граф Тn-1 является остовом минимального веса в графе (G,w).
Билет 6 Остов минимального веса Пусть G — граф. и1: EG —> R — вещественнозначная функция, ставящая в соответствие каждому ребру е положительное (или неотрицательное) число w(e) — вес ребра е. Пару (G, и) назовем взвешенным графом. Под длиной (или весом) любого подграфа взвешенного графа будем понимать сумму весов его ребер.
Рассмотрим следующую задачу: по взвешенном связном графе требуется найти остов минимального веса, эта задача возникает при проектировании линий электропередачи, трубопроводов, дорог и т. п., когда требуется заданные центры соединить некоторой системой каналов связи так, чтобы любые два центра были связаны либо непосредственно соединяющим их каналом, либо через другие центры и каналы, и чтобы общая длина (или, например, стоимость) каналов связи была минимальной, В этой ситуации заданные центры можно считать вершинами полного графа с весами ребер, равными длинам (стоимости) соединяющих эти центры каналов. Тогда искомая сеть будет кратчайшим остовным подграфом полного графа. Очевидно, что этот кратчайший остовный подграф должен быть деревом. Поскольку полный граф К„ содержит п" " различных остовных деревьев, то решение этой задачи «слепым» перебором вариантов потребовало бы чрезвычайно больших вычислений даже при относительно малых П . Однако для ее решения имеются эффективные алгоритмы. Опишем два из них —- алгоритмы Дж. Краскала (1956 г.) и Р. Прима (1957 г.), применимые к произвольному связному графу. Задача об остове минимального веса (о кратчайшем остове): в связном взвешенном графе ((;, w) порядка п найти остов минимального веса. Алгоритм Прима отличается от алгоритма Краскала только тем, что на каждом этапе строится не просто ациклический граф, но дерево. Именно: 1. Выбираем ребро e1=ab минимального веса и строим дерево T1, полагая VT1={a,b} и ET1={e1}. 2, Если дерево Ti, порядка i+1 уже построено и i < п - 1, то среди ребер, соединяющих вершины этого дерева с вершинами графа G, не входящими в Ti выбираем ребро ei , минимального веса. Строим дерево Ti+1, присоединяя к Ti, ребро еi+1 , вместе с его не входящим в Ti концом.
2
 .
Теорема Менгера и ее варианты. Пусть u
и v –
несмежные вершины в графе G.
Наименьшее число вершин в множестве,
разделяющим u и v,
равно наибольшему числу
вершинно-непересекающихся
простых <u,v>-цепей.
(Доказательство теоремы можно найти в
[1] стр. 215-217) Варианты
теормы Менгера. Теорема
Менгера представляет собой весьма общий
факт, который в разных формулировках
встречается в различных областях
математики.
Вариант
1. Для любых двух несмежных
вершин u и v графа G наибольшее
число реберно-непересекающихся
<u,v>-цепей равно наименьшему числу
ребер в (u,v)-разрезе (разделяющее множество
ребер).
Вариант
2. Чтобы граф G был
k-связным,
необходимо и достаточно, чтобы любые
две несмежные вершины были соединены
не менее чем k
вершинно-непересекающимися простыми
цепями.
Наша
цель состоит в том чтобы написать
программудля решения задачи нахождения
для каждой пары вершин графа наибольшего
числа реберно-непересекающихся
<u,v>-цепей.
.
Теорема Менгера и ее варианты. Пусть u
и v –
несмежные вершины в графе G.
Наименьшее число вершин в множестве,
разделяющим u и v,
равно наибольшему числу
вершинно-непересекающихся
простых <u,v>-цепей.
(Доказательство теоремы можно найти в
[1] стр. 215-217) Варианты
теормы Менгера. Теорема
Менгера представляет собой весьма общий
факт, который в разных формулировках
встречается в различных областях
математики.
Вариант
1. Для любых двух несмежных
вершин u и v графа G наибольшее
число реберно-непересекающихся
<u,v>-цепей равно наименьшему числу
ребер в (u,v)-разрезе (разделяющее множество
ребер).
Вариант
2. Чтобы граф G был
k-связным,
необходимо и достаточно, чтобы любые
две несмежные вершины были соединены
не менее чем k
вершинно-непересекающимися простыми
цепями.
Наша
цель состоит в том чтобы написать
программудля решения задачи нахождения
для каждой пары вершин графа наибольшего
числа реберно-непересекающихся
<u,v>-цепей.
БИЛЕТ
7
1.
Связность графов. Вершинная и реберная
связность.
Вершинной
связностью
![]() графа
графа
![]() называется
наименьшее число вершин, удаление
которых приводит к несвязному или
тривиальному графу.
называется
наименьшее число вершин, удаление
которых приводит к несвязному или
тривиальному графу.
Реберной
связностью
![]() графа
называется
наименьшее количество ребер, удаление
которых приводит к несвязному или
тривиальному графу.
графа
называется
наименьшее количество ребер, удаление
которых приводит к несвязному или
тривиальному графу.
Связь между , и минимальной степенью вершины
Пускай
минимальная степень вершины графа
обозначается
буквой
![]() .
Тогда:
.
Тогда:
Теорема:
Для
любого графа
справедливо
следующее неравенство:
|
Док-во: |
Полный
граф.
Теорема: Для
любых натуральных чисел
Доказательство: Граф,
в котором
Рассмотрим
граф
,
являющийся объединением двух полных
графов
2.
Число всех отображений, число инъективных
и биективных отображений
*Рассмотрим построение f , как поэтапный процесс. На первом шаге выбираем f(x1) и т.д. На каждом из m шагов имеется n возможностей. Таким образом, общее кол-во разных последовательностей выборов равно nm . Разным последовательностям выборов соответствуют разные функции. Примеры: 1. Удобно представлять отображение как раскладывание m шаров в n различных ящиков. Утверждение: Число всех инъективных отображений равно [n]m. *Как и при док-ве 1-ого утверждения, для выбора f(x1) имеется n возможностей. Но после этого для выбора f(x2) в Y \{f(x1)} имеется уже не n, а n-1 возможностей, для выбора f(x3) имеется n-2 возможностей, ит.д. Следовательно, общее число различных инъективных отображений равно n(n-1)(n-2)…(n-m+1) = [n]m. Примеры: 1. Инъективное отображение удобно представлять как раскладывание m помеченных шаров в n различных ящиков таким образом, чтобы в каждом ящике было более одного шара. Следствие: Число всех биективных отображений равно n! при m=n и равно 0 при m не= n. Пример Число перестановок чисел 1,2…n равно n!. |
БИЛЕТ 8 1. Планарные графы. Формула Эйлера для полиэдров. Плоским графом назовем граф, вершины которого являются точками плоскости, а ребра –непрерывными плоскими линиями без самопересечений, соединяющими соответствующие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины. Три первых графа на рис. 5.1 являются плоскими.
Л юбой
граф, изоморфный плоскому графу,
называется планарным.
Граф
K4,
изображенный последним на рис. 5.1,
является планарным, так как он изоморфен
второму и третьему графам на рис. 5.1.
юбой
граф, изоморфный плоскому графу,
называется планарным.
Граф
K4,
изображенный последним на рис. 5.1,
является планарным, так как он изоморфен
второму и третьему графам на рис. 5.1.
Очевидны следующие утверждения: 1) всякий подграф планарного графа планарен;
2) граф планарен тогда и только тогда, когда каждая его связная компонента – планарный граф. О планарных графах говорят, что они укладываются на плоскости (имеют плоскую укладку).
Дадим определение укладки графа в произвольное пространство. Прежде всего введем понятие жордановой кривой, под которой будем понимать непрерывную, (спрямляемую) линию, не имеющую самопересечений.
Будем говорить, что граф G укладывается в пространство L, если существует такое отображение вершин и ребер графа G соответственно в точки и жордановы кривые этого пространства, что различным вершинам соответствуют различные точки, а кривые, соответствующие различным ребрам, пересекаются только в инцидентных этим ребрам вершинах. Изображенный таким образом граф называется укладкой графа G в пространство L.
Теорема Каждый граф укладывается в трехмерное пространство E3 .

Все
вершины графа G
помещаем в различные точки оси ОХ.
Из пучка плоскостей, проходящих через
эту ось, выберем |EG|
различных плоскостей. Далее, каждое
ребро uv
EG
изображаем в соответствующей плоскости
полуокружностью, проходящей через
вершины u
и v.
Понятно, что в результате получаем
укладку графа G
в
E3,
так как все ребра лежат в разных плоскостях
и потому не пересекаются во внутренних
точках.
Все
вершины графа G
помещаем в различные точки оси ОХ.
Из пучка плоскостей, проходящих через
эту ось, выберем |EG|
различных плоскостей. Далее, каждое
ребро uv
EG
изображаем в соответствующей плоскости
полуокружностью, проходящей через
вершины u
и v.
Понятно, что в результате получаем
укладку графа G
в
E3,
так как все ребра лежат в разных плоскостях
и потому не пересекаются во внутренних
точках.
Теорема Граф укладывается на сфере тогда и только тогда, когда он планарен.
Для доказательства этой теоремы достаточно рассмотреть стереографическую проекцию (рис. 5.2). Пусть граф G уложен на сфере. Проведем плоскость Q, касательную к сфере, так, чтобы северный полюс N (точка, диаметрально противоположная точке касания) не лежал на ребре и не совпадал с вершиной графа G. Теперь рассмотрим граф G’, полученный стереографической проекцией графа G из точки N на плоскость Q. Поскольку существует взаимно однозначное (биективное) соответствие между точками сферы, отличными от N, и их стереографическими проекциями, то граф G’ плоский и изоморфен графу G. Следовательно, G – планарный граф. Обратное утверждение доказывается аналогично с учетом установленной биекции.
Определения плоского и планарного графов и многие другие утверждения этих пунктов сохраняются применительно к мульти- и псевдографам.
Теорема (формула Л. Эйлера, 1758 г.). Для всякого связного плоского графа верно равенство n – m + f = 2.
Пусть G – связный плоский n-вершинный граф. Рассмотрим некоторый остов T этого графа. Очевидно, что дерево T имеет одну грань (внешнюю) и n вершин. В то же время известно, что число ребер дерева T равно n – 1. Поэтому для графа T формула (5.1) верна. Теперь будем поочередно добавлять к T недостающие ребра графа G. При этом на каждом шаге число вершин, естественно, не меняется, а число ребер и число граней увеличивается на единицу на основании свойства 5.5. Следовательно, формула (5.1) будет верна для всякого графа, получающегося в результате таких операций (шагов), а поэтому она верна и для графа G, которым заканчивается вся эта процедура.
Из теоремы Эйлера вытекает ряд интересных следствий. Прежде всего, рассмотрим в трехмерном пространстве выпуклый многогранник с n вершинами, m ребрами и f гранями. Очевидно, что спроектировав этот многогранник на описанную около него сферу, далее уложив его так, чтобы северный полюс находился внутри одной из граней, и, произведя затем стереографическую проекцию, получим связный плоский граф. Поэтому справедливо следующее следствие.
Следствие У всякого выпуклого многогранника сумма числа вершин n и числа граней f без числа ребер m равна двум: n – m + f = 2.
Доказательство именно этой формулы и было впервые опубликовано Л. Эйлером в 1758 г. в «Записках Петербургской академии наук».
Следствие Число граней любой плоской укладки связного планарного (n, m)-графа постоянно и равно m – n + 2.
Другими словами, число f является инвариантом планарного (n, m)-графа, т.е. не зависит от способа укладки этого графа на плоскости.
Следствие Для связного планарного (n, m)-графа m 3n – 6 при n 3.
Не теряя общности, будем считать, что G – плоский граф. Прежде всего заметим, что всякое ребро плоского графа либо разделяет две различные грани, либо является мостом (см. свойство 5.6). Поскольку G – граф без петель и кратных ребер, то всякая грань ограничена, по крайней мере, тремя ребрами (исключение составляет лишь случай, когда G – дерево с тремя вершинами, но для такого графа неравенство m 3n – 6 очевидно). Поэтому число 3f является оценкой снизу удвоенного числа ребер графа G, т.е. 3f 2. Отсюда, учитывая формулу Эйлера f = m – n + 2, получаем требуемое неравенство.
Равенство в указанном следствии достигается на плоских связных графах, в которых каждая грань, в том числе и внешняя, является треугольной (другие названия треугольной грани – треугольник, 3-грань). Такие графы называются плоскими триангуляциями.
Следствие Для всякой плоской (n, m)-триангуляции, m = 3n – 6.
Из следствия 5.9 сразу же получаем утверждение 5.11.
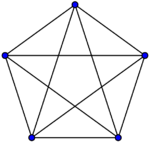
Утверждение Граф K5 не планарен.
Действительно, для полного графа K5 имеем n = 5, m = 10. Поэтому неравенство 3n – 6 m превращается в неверное: 9 > 10, т.е. граф K5 не может быть планарным.
Утверждение. Граф K3,3 не планарен.
Для рассматриваемого графа n = 6, m = 9. Поэтому, если бы он был планарным, то для любой его плоской укладки выполнялось бы f = 5 согласно следствию 5.8. В то же время всякая грань двудольного графа K3,3 должна быть ограничена, по меньшей мере, четырьмя ребрами. Следовательно, 2m 4f, т.е. 18 > 20. Противоречие.
Как мы увидим далее, графы K5 и K3,3 являются минимальными непланарными графами и играют важную роль во многих критериях планарности.

 аконец,
предположим, что граф
содержит
множество из
аконец,
предположим, что граф
содержит
множество из
 конечных множеств (все элементы в
конечных множеств (все элементы в
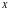 и
и
 различимы). Утверждение:
Число всех отображений
равно
nn
.
различимы). Утверждение:
Число всех отображений
равно
nn
.