42Приближенное интегрирование

Приближенное интегрирование – раздел вычислительной математики, занимающийся приближенным решением дифференциальных уравнений.

Первой задачей приближенного интегрирования является приближенное вычисление интегралов (оно соответствует решению простейшего обыкновенного дифференциального уравнения y'=f(x)).

В тех случаях, когда точное интегрирование невозможно (интеграл не может быть выражен в известных функциях), применяются аналитические методы приближенного интегрирования, заключающиеся в том, что подынтегральная функция заменяется другой, интеграл от которой вычисляется более или менее легко. В качестве такой функции часто берут интерполяционный многочлен.

Приближенное интегрирование применяется также в тех случаях, когда интегрируемая функция задана таблицей или графиком или если она быстрее, чем интерполяционный многочлен, приводит к цели (с заданной точностью). Тогда применяют и графические методы (построение графика первообразной функции по графику подынтегральной функции, а также различные математические машины и приборы – вычислительные машины, интеграторы, планиметры и т.п.).

Основной задачей приближенного интегрирования является приближенное решение дифференциальных уравнений весьма общего вида. Здесь также существуют как аналитические, так и численные методы решения задач.

43Восстановление линейной зависимости между двумя переменными

          Начнем с задачи точечного и доверительного оценивания линейной функции одной переменной.

          Исходные данные – набор n пар чисел (t_k , x_k), k = 1,2,…,n, где t_k – независимая переменная (например, время), а x_k – зависимая (например, индекс инфляции, курс доллара США, объем месячного производства или размер дневной выручки торговой точки). Предполагается, что переменные связаны зависимостью

x_k = a (t_k - t_ср)+ b + e_k , k = 1,2,…,n,

где a и b – параметры, неизвестные статистику и подлежащие оцениванию, а e_k – погрешности, искажающие зависимость. Среднее арифметическое моментов времени

t_ср = (t₁ + t₂ +…+t_n )/n

введено в модель для облегчения дальнейших выкладок.

          Обычно оценивают параметры a и b линейной зависимости методом наименьших квадратов. Затем восстановленную зависимость используют, например, для точечного и интервального прогнозирования.

          Как известно, метод наименьших квадратов был разработан великим немецким математиком К. Гауссом в 1794 г. Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость x от t, следует  рассмотреть функцию двух переменных

Оценки метода наименьших квадратов - это такие значения a* и b*, при которых функция f(a,b)достигает минимума по всем значениям аргументов.

          Чтобы найти эти оценки, надо вычислить частные производные от функции f(a,b) по аргументамa и b, приравнять их 0, затем из полученных уравнений найти оценки: Имеем:

Преобразуем правые части полученных соотношений. Вынесем за знак суммы общие множители 2 и (-1). Затем рассмотрим слагаемые. Раскроем скобки в первом выражении, получим, что каждое слагаемое разбивается на три. Во втором выражении также каждое слагаемое есть сумма трех. Значит, каждая из сумм разбивается на три суммы. Имеем:

Приравняем частные производные 0. Тогда в полученных уравнениях можно сократить множитель (-2). Поскольку

                 (1)

уравнения приобретают вид

Следовательно, оценки метода наименьших квадратов имеют вид

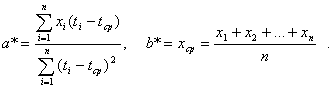  (2)

          В силу соотношения (1) оценку а* можно записать в более симметричном виде:

Эту оценку нетрудно преобразовать и к виду

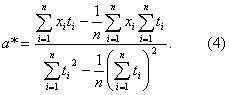
Следовательно, восстановленная функция, с помощью которой можно прогнозировать и интерполировать, имеет вид

x*(t) = a*(t - t_ср)+ b*.

          Обратим внимание на то, что использование t_ср  в последней формуле ничуть не ограничивает ее общность. Сравним с моделью вида

x_k = c t_k+ d + e_k , k = 1,2,…,n.

Ясно, что

Аналогичным образом связаны оценки параметров:

          Для получения оценок параметров и прогностической формулы нет необходимости обращаться к какой-либо вероятностной модели. Однако для того, чтобы изучать погрешности оценок параметров и восстановленной функции, т.е. строить доверительные интервалы для a*, b* и x*(t), подобная модель необходима.

          Непараметрическая вероятностная модель. Пусть значения независимой переменной tдетерминированы, а погрешности e_k , k = 1,2,…,n, - независимые одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией  неизвестной статистику.

          В дальнейшем неоднократно будем использовать Центральную Предельную Теорему (ЦПТ) теории вероятностей для величин e_k , k = 1,2,…,n (с весами), поэтому для выполнения ее условий необходимо предположить, например, что погрешности e_k , k = 1,2,…,n, финитны или имеют конечный третий абсолютный момент. Однако заострять внимание на этих внутриматематических "условиях регулярности" нет необходимости.

Дополнительные вопросы

1. Определение скалярного произведения

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

  

Формуле   (6.1)   можно   придать   иной   вид.   Так   как | a| cos=пр _ba, (см. рис.14), a |b| cos = пр _ab, то получаем:

      

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

. Свойства скалярного произведения

    1. Скалярное произведение обладает переместительным свойством: ab=ba

  

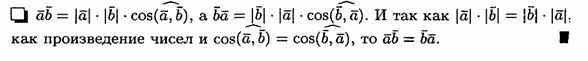
Решение:                                                              

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а 0b, то а  b

.

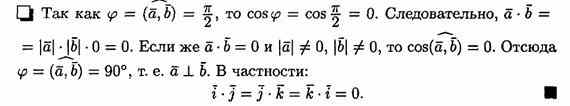
Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

   

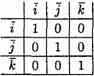
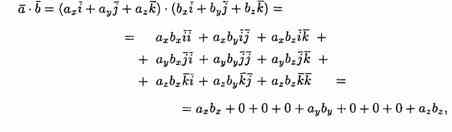
    т.е

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

2. Определение векторного произведения

Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму векторуb виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

      

 Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. са и сb;

2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и bкак на сторонах (см. рис. 17), т. е. 

3.Векторы a, b и с образуют правую тройку.

Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k,    j х k = i,    k х i = j.  Докажем, например, что iхj=k.

1) ki, kj;

2) |k|=1, но | i x j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).

. Свойства векторного произведения

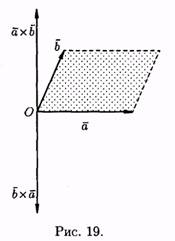
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).

 Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , bxaпротивоположной ориентации). Стало быть axb = -(bxa ).

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. (а хb ) = (а ) х b = а х (b ).

Пусть >0. Вектор (ахb ) перпендикулярен векторам а и b . Вектор ( а)хb также перпендикулярен векторам а и b (векторы а, а лежат в одной плоскости). Значит, векторы(ахb ) и ( а)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

Поэтому (a хb )= ахb . Аналогично доказывается при <0.

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0.

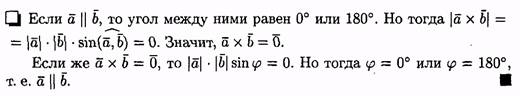
В частности, i *i =j *j =k *k =0.

4. Векторное произведение обладает распределительным свойством:

(a+b) хс= ахс+b хс.

Примем без доказательства.

. Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов i , j и k :

если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».

Пусть заданы два вектора а=а_хi +a_yj +a_zk и b =b_xi +b_yj +b_zk . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

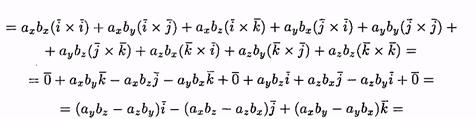
Полученную формулу можно записать еще короче:

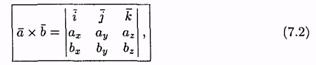
так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки.Равенство (7.2) легко запоминается.

^{Дополнительный вопрос}