5. Свойства вероятности.

1) Вероятность невозможного события равна 0, т.е. . Док-во: .

2) Вероятность достоверного события равна 1, т.е. . Док-во:

.3) Для любого события вероятность лежит в пределах от 0 до 1, т.е. . Д-во: ; .

4)(Теорема сложения вероятностей): если события А и В несовместимы, то вероятность их суммы равна сумме вероятностей этих событий, т.е. Р(А+В)=Р(А)+Р(В). Док-во:

5)(обобщенная теорема сложения вероятностей) . Док-во:

6.Условная вероятность.Независимость.

Опр. Условной вероятностью события B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение , (реже ). . .

Теорема (умножение вероятностей): .

Теорема (обобщенная теорема умножения).

.

Доказательство:

.

Опр. События А и В называются независимыми, если .

Свойство. События А и В независимы тогда и только тогда когда P(B/A)=P(B). . Пусть P(B/A)=P(B), тогда А и В независимы.

Опр. События А₁,А₂,…,А_n называются независимыми (или независимыми в совокупности), если (для i≠j; i,j {1,2,3,…,n})–попарная независимость событий; , …,

.

7.Формула полной вероятности и Байеса.

Теорема 1. Если события Н₁, Н₂,…,Н_n образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности: , или . ▲Так как события образуют полную группу, то можно записать . Событие А может произойти только с одним из событий H_i, i {1,2,…,n}, то А=АН₁+АН₂+…+АН_n. По теореме сложения вероятностей ▲

Теорема 2. Пусть события Н₁, Н₂, …, Н_n образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса:

,

Доказательство: По теореме умножения вероятностей

. Отсюда находим вероятность . Остается в знаменателе подставить вместо —формула полной вероятности.

10.Локальная и интегральная теоремы Муавра-Лапласа.

Теорема (локальная теорема Муавра-Лапласа).

Если вероятность появления события А в каждом отдельном испытании постоянная и отлична от 0 и 1, т.е. 0<p<1, то вероятность того, что событие А появится ровно k раз в n независимых испытаниях.

, где ; , q=1-p.

Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х).

Теорема (интегральная теорема Муавра-Лапласа).

Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0<p<1, то вероятность того, что событие А появится от k₁ до k₂ раз в n независимых испытаниях определяется выражением: , где —функция Лапласа, , , .

Функция Лапласа—нечетная, т.е. . Значения находят по таблице.

6)(теорема сложения k слагаемых) Если события А₁, А₂,…, А_k попарно несовместимы, то .

7) Если событие А влечет В, т.е. , то Р(А)≤Р(В). Док-во: В=А+B\A; P(B)=P(A)+P(B\A) => P(B)≥P(A)

8) если событие А влечет В, то P(B\A)=P(B)-P(A)

9) Вероятность события, противоположного событию А, т.е. . Док-во: , .

10) если события Н₁, Н₂,…,Н_k образуют полную группу, то . Док-во: т.к. , , то по свойству 6: .

Случай 2. Пусть Х и Y—непрерывные случайные величины.

Теорема. Если Х и Y—независимые непрерывные случайные величины, то случайная величина Z=X+Y—также непрерывна, причем плотность распределения случайной величины Z —формула свертки.

Опр. Плотность распределения суммы независимых случайных величин называется композицией.

Замечание. Если возможные значения X и Y неотрицательны, то формула свертки .

Опр. Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон распределения (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойствами устойчивости, т.е. композиция нормальных законов также имеет нормальное распределение, причем математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых: , .

В частности, если Х~N(0,1) и Y~N(0,1), то Z=X+Y~N(0,2).

Опр. События А и В наз. несовместимыми, если . Опр. Говорят, что событие А влечет событие В, если А является подмножеством В (когда происходит А, происходит В). Опр. Событие наз. противоположным к событию А. происходит тогда, когда А не происходит. Опр. Говорят, что события Н₁,Н₂,…,Н_n образуют полную группу, если Н₁+Н₂+…+Н_n=Ω (т.е. Н₁, Н₂,…,Н_n–несовместимы, т.е. Н_i Н_j= , если i≠j). Предположим, что производится некоторый случайный эксперимент, рез-т кот. описывается пространством Ω. Произведем N экспериментов. Пусть А—некоторое событие ( ), N(A)—число тех экспериментов, в которых произошло событие А. Опр. Число наз. относительной частотой события А. Свойства относительных частот. 1) Относительная частота произвольного события А неотрицательна, т.е. . 2) Относительная частота достоверного события равна 1. . 3)(аддитивность) Относительная частота суммы несовместимых событий равна сумме относительных частот этих событий. ; .

Опр. Вероятностью события А наз. число . Сделаем следующие предположения: 1) Пространство элементарных исходов конечно. 2) Все элементарные исходы равновозможны (равновероятны), т.е. .Рассмотрим некоторое событие , где k≤n, тогда вероятность события А Опр.(классическое определение вероятности): Если пространство элементарных исходов конечно, а все элементарные исходы равновероятны, то вероятностью события А наз. отношение числа элементарных исходов, благоприятствующих событию А, к числу всех возможных элементарных исходов:

Геометрические вероятности. Предположим, что на числовой оси имеется некоторый отрезок [a,b] и на этот отрезок наудачу бросается точка. Найти вероятность того, что эта точка попадет на [c,d] [a,b]. — геометрическая вероятность на прямой. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g G определяется равенством: — геометрическая вероятность на плоскости. Пусть в пространстве имеется фигура r, составляющая часть фигуры L. На фигуру L наудачу брошена точка. Вероятность попадания точки на фигуру r определяется равенством: —геометрическая вероятность в пространстве. Замечание. Недостатком классического определения вероятности является то, что оно не применимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности.

О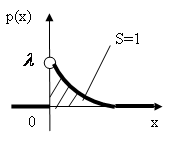 пр. Говорят, что случайная величина Х имеет показательное (экопоненциальное) распределение с параметром λ>0, если она непрерывна и имеет плотность распределения ; обозначают Х~M(λ).

Найдем функцию распределения показательно распределенной случайной величины Х.

а) x≤0 .

б) x>0

Т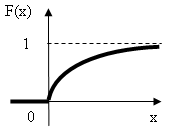 аким образом

О пр. Говорят, что случайная величинf Х имеет нормальное распределение с параметрами a, , если она непрерывна и имеет плотность . Обозначение Х~N(a, ), те Х имеет нормальное распределение с параметрами a, G².

График плотности нормально распределенной случайной величины имеет вид:

Предположим, что случайная величина . Вероятность, что Пусть .

.

, где —функция Лапласа.

Замечание. Необходимо отметить, что φ(t)—четная функция, т.е. φ(-х)=φ(х); функция Лапласа —нечетная, т.е. ; функция стандартного нормального распределения N(x) обладает свойством N(x)+N(-x)=1.

3. .

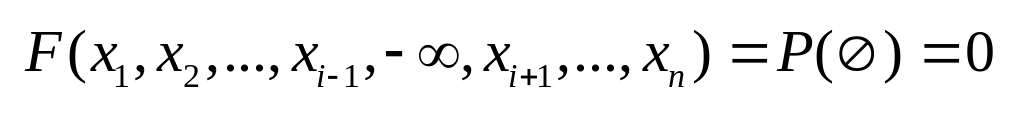▲ =0▲

▲

= .▲

Опр. Случайный вектор называется дискретным, если все его компоненты—дискретные случайные величины.

Опр. Случайный вектор называется непрерывным, если существует неотрицательная функция , называется плотностью распределения случайных величин такая, что функция распределения .

Свойства плотности распределения случайного вектора.

1.

2. .

.

Теорема 1. Пусть —непрерывный случайный вектор. Тогда случайные величины и — непрерывны, причем , .

3. , где —множество из пространства .