
- •1.Случайные события. Достоверное и невозможное события. Совместимые, несовместимые и противоположные события.
- •2.Определение классической вероятности. Полная группа событий, элементарные события.
- •3.Статистическое определение вероятности. Частота события.
- •4.Основные формулы комбинаторики. Размещения, сочетания и перестановки.
- •5.Теорема сложения вероятностей совместимых событий. Сумма и произведение событий.
- •6.Теорема умножения вероятностей. Зависимые и независимые события, условная вероятность.
- •7. Теорема сложения вероятностей несовместимых событий. Сумма событий.
- •8.Формула полной вероятности. Произведение событий. Формула Байеса.
- •9.Понятие св. Дискретные и непрерывные св.
- •10.Закон распределения дискретной св. Примеры.
- •11.Функция распределения св и ёё свойства.
- •12.Мат.Ожидание дсв. Теорема о мат.Ожидании.
- •13. Свойства мат.Ожидания дсв.
- •18.Плотность вероятности нсв и её свойства.
- •19.Мат.Ожидание,дисперсия и среднее квадратическое отклонение нсв
- •20 Биноминальное распределение
- •21.Геометрическое распределение
- •22.Равномерное распределение непрерывной случайной величины
- •24.Закон нормального распределения
- •26.Основные понятия многомерных св.
- •27.Закон распределения вероятностей двумерной дсв.
- •28.Функция распределения двумерной св и её свойства.
- •33.Генеральная и выборочная совокупности.
- •34.Повторная и бесповторная выборки. Репрезентативная выборка.
- •35.Способы отбора в выборочную совокупность.
- •36.Стат.Распределение выборки или вариационный ряд.
- •37.Эмпирическая функция распределения и её свойства.
- •38.Графическое представление выборки. Полигон и гистограмма.
- •39. Стат.Оценки параметров распределения. Несмещенные, эффективные и состоятельные оценки.
- •40.Генеральная и выборочная средняя.
- •41.Генеральная и выборочная дисперсия.
- •42.Оценка генеральной дисперсии по исправленной выборочной дисперсии.
- •43.Вычисление числовых характеристик вариационного ряда с помощью условных вариант.
- •44.Метод моментов для оценки вариационного ряда.
- •45.Метод наибольшего правдоподобия для оценки параметров распределения.
- •46. Метод наибольшего правдоподобия для биноминального распределения
- •47. Метод наибольшего правдоподобия для пуассоновского распределения
- •48.Показательный (экспоненциальный) закон распределения
- •49.Интервальные оценки числовых характеристик
45.Метод наибольшего правдоподобия для оценки параметров распределения.
Метод наибольшего правдоподобия в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия.
Пусть есть выборка
![]() из распределения
из распределения
![]() ,
где
,
где
![]() -неизвестный
параметр. Пусть
-неизвестный
параметр. Пусть
![]() -
функция правдоподобия. Точечная оценка
-
функция правдоподобия. Точечная оценка
![]() называется оцеенкой
наибольшего правдоподобия параметра
θ. Таким образом оценка максимального
правдоподобия — это такая оценка,
которая максимизирует функцию
правдоподобия при фиксированной
реализации выборки.
называется оцеенкой
наибольшего правдоподобия параметра
θ. Таким образом оценка максимального
правдоподобия — это такая оценка,
которая максимизирует функцию
правдоподобия при фиксированной
реализации выборки.
46. Метод наибольшего правдоподобия для биноминального распределения
Биномиальное
распределение
имеет
дискретная случайная величина X, если
она принимает значения 0, 1, …, n со
следующими вероятностями:
![]() где n, p – параметры распределения (0 ≤
p ≤ 1), q = 1 – p. Числовые характеристики
биномиального распределения: mХ
=np,
DХ
=nqp.
Условия возникновения. Проводится n
одинаковых независимых, в каждом из
которых событие А появляется с вероятностью
р. Случайная величина Х – число опытов,
в которых произошло событие А (см. теорему
о повторении опытов).
где n, p – параметры распределения (0 ≤
p ≤ 1), q = 1 – p. Числовые характеристики
биномиального распределения: mХ
=np,
DХ
=nqp.
Условия возникновения. Проводится n
одинаковых независимых, в каждом из
которых событие А появляется с вероятностью
р. Случайная величина Х – число опытов,
в которых произошло событие А (см. теорему
о повторении опытов).
47. Метод наибольшего правдоподобия для пуассоновского распределения
Распределение
Пуассона
имеет
дискретная случайная величина Х, если
она принимает значения 0, 1, …, ∞
со
следующими вероятностями:
![]() где a – параметр распределения (a > 0).
Числовые характеристики пуассоновской
случайной величины: mХ
=a,
DХ
=a.
(6.7) Условия возникновения: 1. Распределение
Пуассона является предельным случаем
биномиального, когда число опытов n
неограниченно увеличивается, а вероятность
p события A в одном опыте стремится к 0,
так что существует предел
где a – параметр распределения (a > 0).
Числовые характеристики пуассоновской
случайной величины: mХ
=a,
DХ
=a.
(6.7) Условия возникновения: 1. Распределение
Пуассона является предельным случаем
биномиального, когда число опытов n
неограниченно увеличивается, а вероятность
p события A в одном опыте стремится к 0,
так что существует предел
![]() .
2. Случайная величина Х – число событий
пуассоновского потока поступивших в
течение интервала τ,
причем параметр а = τλ,
где λ
–
интенсивность потока.
.
2. Случайная величина Х – число событий
пуассоновского потока поступивших в
течение интервала τ,
причем параметр а = τλ,
где λ
–
интенсивность потока.
МЕТОД НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ! ! !
Согласно
данному методу оценки
![]() ,
…,
,
…,
![]() получаются из условия максимума по
параметрам Q1, ..., Qm положительной функции
правдоподобия L(x1,...,xn,Q1,...,Qm). Если случайная
величина X непрерывна, а значения xi
независимы, то L(x1,…,xn,
Q1,…,
Qm
)=
получаются из условия максимума по
параметрам Q1, ..., Qm положительной функции
правдоподобия L(x1,...,xn,Q1,...,Qm). Если случайная
величина X непрерывна, а значения xi
независимы, то L(x1,…,xn,
Q1,…,
Qm
)=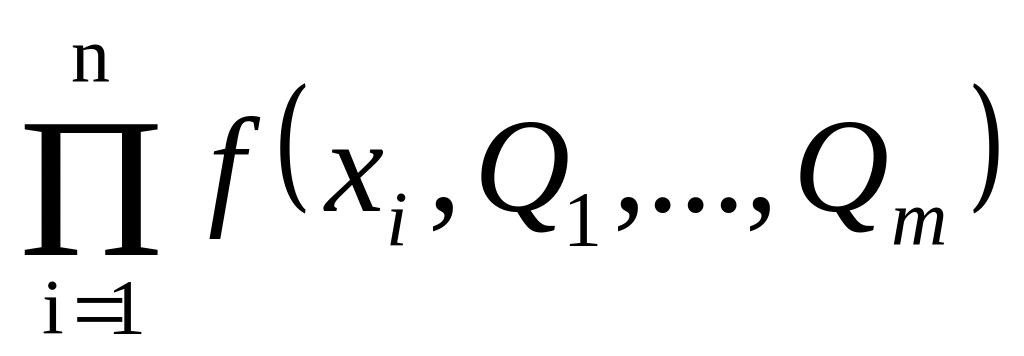 Если случайная величина X дискретна и
принимает независимые значения xi с
вероятностями p(X =xi)= pi(xi,Q1,...,Qm), то функция
правдоподобия равна L(x1,…,xn,
Q1,…,
Qm
)=
Если случайная величина X дискретна и
принимает независимые значения xi с
вероятностями p(X =xi)= pi(xi,Q1,...,Qm), то функция
правдоподобия равна L(x1,…,xn,
Q1,…,
Qm
)=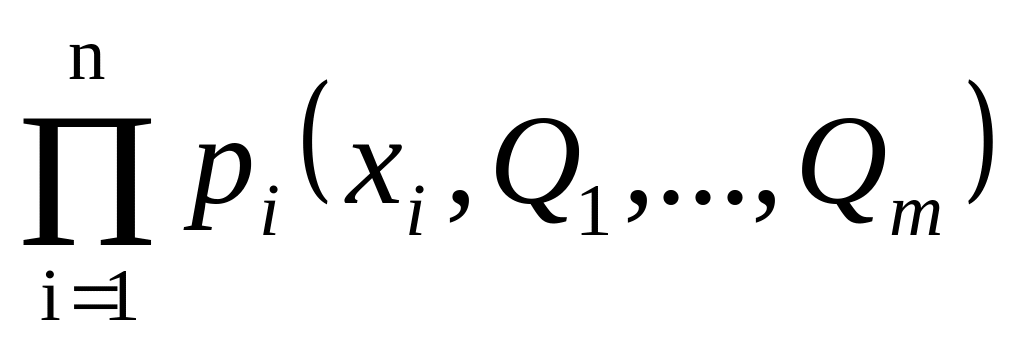 Система уравнений согласно этому методу
может записываться в двух видах:
Система уравнений согласно этому методу
может записываться в двух видах:
![]() i=1,
2, …, m,
или
i=1,
2, …, m,
или
![]() i=1,
2, …, m.
i=1,
2, …, m.
Найденные корни выбранной системы уравнений являются оценками , …, неизвестных параметров Q1, ..., Qm.
48.Показательный (экспоненциальный) закон распределения
Рассматривается
пример поиска методом максимального
правдоподобия оценки параметра
экспоненциального распределения
случайной величины,для которой функция
плотности имеет вид
![]() К
характеристикам экспоненциального
распределения относятся математическое
ожидание и дисперсия :
К
характеристикам экспоненциального
распределения относятся математическое
ожидание и дисперсия :![]()
![]() Построить
доверительный интервал с надежностью
g =1– a для оценки m 1
математического
ожидания m1
случайной
величины х,
имеющей экспоненциальное распределение
с функцией плотности f(x,
l)
= lехр(–
lх).
Построить
доверительный интервал с надежностью
g =1– a для оценки m 1
математического
ожидания m1
случайной
величины х,
имеющей экспоненциальное распределение
с функцией плотности f(x,
l)
= lехр(–
lх).
Решение. Известно, что для экспоненциального закона распределения математическое ожидание т1 = 1/l, а дисперсия т2 = 1/l2. Обозначим через l оценку параметра l. Определим оценку математического ожидания m 1, вспомогательную переменную у, производную от логарифма функции правдоподобия:
m 1 = (х1+ х2+ … + хп)/п = 1/l ; М(l ) = l; т1 = М(1/l );
у =
![]() ;
;
![]()
Оценка m 1 параметра т1 является состоятельной и несмещенной, следовательно: М(у)=М(l –1 – х) = 0; значение А2 = М(l –1 – х)2 =l –2 конечно. Тогда случайная величина
w
=
![]()
распределена нормально с параметрами 0 и 1.
Нормальное распределение симметрично, поэтому границы интервала следует выбрать симметрично относительно нулевой точки. Вероятность g =1 – a того, что модуль величины w не превысит некоторого заданного значения d , составит
![]() где Ф(d ) – значение
функции нормального распределения в
точке d Величина d равна квантили
u1–a
/2
стандартного нормального распределения
уровня 1– a /2. Значение абсолютной
погрешности оценивания E
= | m1
–
m 1|
=d /(l n0,5)
= u1–
a /2 /(l
n0,5).
Итак, имея достаточный объем выборки
ЭД и задаваясь определенным уровнем
надежности g можно определить доверительный
интервал t0
= m 1
– Е,
t1
= m 1
+ Е,
который с заданной вероятность содержит
неизвестный параметр т1.
Аналогичные результаты для некоторых
параметров распределения можно получить,
используя более простые рассуждения.
где Ф(d ) – значение
функции нормального распределения в
точке d Величина d равна квантили
u1–a
/2
стандартного нормального распределения
уровня 1– a /2. Значение абсолютной
погрешности оценивания E
= | m1
–
m 1|
=d /(l n0,5)
= u1–
a /2 /(l
n0,5).
Итак, имея достаточный объем выборки
ЭД и задаваясь определенным уровнем
надежности g можно определить доверительный
интервал t0
= m 1
– Е,
t1
= m 1
+ Е,
который с заданной вероятность содержит
неизвестный параметр т1.
Аналогичные результаты для некоторых
параметров распределения можно получить,
используя более простые рассуждения.
