
1.6 Компьютерная геометрия и графика
1. Уравнение прямой по точке и вектору нормали
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки:
![]()
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
На плоскости записанное выше уравнение прямой упрощается:
![]()
если х1 ¹ х2 и х = х1, еслих1 = х2.
Дробь
![]() =
k
называется угловым
коэффициентом
прямой.
=
k
называется угловым
коэффициентом
прямой.
Уравнение прямой по точке и угловому коэффициенту
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:

и
обозначить
![]() ,
то полученное уравнение называется
,
то полученное уравнение называется
уравнением прямой с угловым коэффициентом k.
Уравнение прямой по точке и направляющему вектору
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение.
Каждый ненулевой вектор
![]() (a1,
a2),
компоненты которого удовлетворяют
условию Аa1
+ Вa2
= 0 называется направляющим вектором
прямой
(a1,
a2),
компоненты которого удовлетворяют
условию Аa1
+ Вa2
= 0 называется направляющим вектором
прямой
Ах + Ву + С = 0.
Нормальное уравнение прямой
Если
обе части уравнения Ах + Ву + С = 0 разделить
на число
![]() ,
которое называется нормирующем
множителем,
то получим
,
которое называется нормирующем
множителем,
то получим
xcosj + ysinj - p = 0 – нормальное уравнение прямой.
Знак ± нормирующего множителя надо выбирать так, чтобы m×С < 0.
р – длина перпендикуляра, опущенного из начала координат на прямую, а j - угол, образованный этим перпендикуляром с положительным направлением оси Ох.
Угол между прямыми на плоскости
Определение. Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как
 .
.
Две прямые параллельны, если k1 = k2.
Две прямые перпендикулярны, если k1 = -1/k2.
Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = lА, В1 = lВ. Если еще и С1 = lС, то прямые совпадают.
Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.
Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
Определение. Прямая, проходящая через точку М1(х1, у1) и перпендикулярная к прямой у = kx + b представляется уравнением:
![]()
2. Общее уравнение плоскости имеет вид
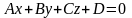 .
.
Построение плоскости означает определение
параметров
 .
Все другие виды уравнения плоскости
легко получить из общего уравнения.
.
Все другие виды уравнения плоскости
легко получить из общего уравнения.
Рассмотрим простейший способ вычисления параметров .
Пусть заданы точка
 ,
лежащая на искомой плоскости, и вектор
,
лежащая на искомой плоскости, и вектор
 ,
ортогональный искомой плоскости.
,
ортогональный искомой плоскости.
Для поиска параметров
воспользуемся тем, что вектор
 ортогонален любому вектору
ортогонален любому вектору
 ,
лежащей на искомой плоскости.
,
лежащей на искомой плоскости.
Из условия ортогональности векторов
(их скалярное произведение равно нулю:
 )
получаем:
)
получаем:

Здесь
 .
.
Нормированное уравнение плоскости
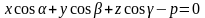
из общего уравнения получается путем замен
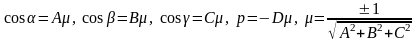 .
.
Знак μ выбирается противоположным знаку D.
Здесь (α, β, γ) – направляющие углы вектора, перпендикулярного искомой плоскости (этот вектор направлен от начала координат в сторону плоскости), и p – расстояние от начала координат до плоскости.
Так же легко получить уравнение плоскости
в отрезках, если известны три отрезка
 ,
отсекаемые плоскостью на осях координат:
,
отсекаемые плоскостью на осях координат:
 .
.
Это уравнение легко можно получить и из общего уравнения, приняв:
a=-D/A, b=-D/B, c=-D/C.
Рассмотрим более сложные в смысле расчетов построения плоскости.
Известна
аксиома – через три разные точки
,
 и
и
 можно построить единственную плоскость.
можно построить единственную плоскость.
Есть разные способы построения этой плоскости.
Способ 1. Векторы
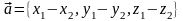 и
и
 параллельны искомой плоскости. Их
векторное произведение
параллельны искомой плоскости. Их
векторное произведение
 ортогонально искомой плоскости.
ортогонально искомой плоскости.
Тогда получили задачу построения плоскости, проходящей через точку перпендикулярно вектору . Это построение рассмотрено выше.
Способ 2. Использовать компланарность
векторов
 ,
,
 и
и
 :
:
 .
.
Раскрыв этот определитель, можно получить общее уравнение плоскости:

Здесь
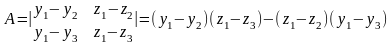 ,
,
 ,
,
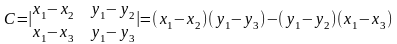 ,
,

Условие компланарности является универсальным методом построения плоскости при различных исходных данных.
3. Понятие пространственной прямой связано с понятием плоскости. Например, прямой является линия пересечения двух плоскостей (аксиома стереометрии). Рассмотрим способы описания прямой.
Способ 1. Общее уравнение прямой представляет собой систему из двух уравнений пересекающихся плоскостей:

Способ
2. Через точку
 можно построить прямую параллельно
некоторому вектору
можно построить прямую параллельно
некоторому вектору
 .
В этом случае уравнение называется
каноническим и имеет вид:
.
В этом случае уравнение называется
каноническим и имеет вид:

и является условием коллинеарности двух векторов:

Если направляющий вектор перпендикулярен какой-либо координатной оси, то соответствующая координата вектора равна нулю. Запись канонического уравнения является символической, и деление на ноль не требуется.
Началом
вектора
 является известная по условию точка
искомой прямой L, а концом - произвольная
точка
является известная по условию точка
искомой прямой L, а концом - произвольная
точка
 этой прямой.
этой прямой.
По этому же способу можно построить
каноническое уравнение прямой, проходящей
через две заданные точки
и
 .
Для этого в предыдущем построении
достаточно принять
.
Для этого в предыдущем построении
достаточно принять
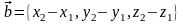 или, что то же самое,
или, что то же самое,
 .
В итоге получим:
.
В итоге получим:
 .
.
Переход от общих уравнений к каноническим требует некоторого усилия. Рассмотрим идею такого перехода. Параметры системы уравнений
представляют
собой два вектора
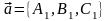 и
и
 ,
перпендикулярных к обеим плоскостям.
Очевидно, что векторы
и
,
перпендикулярных к обеим плоскостям.
Очевидно, что векторы
и
 перпендикулярны и прямой, лежащей на
пересечении этих плоскостей. Найдем
вектор
,
который перпендикулярен векторам
и
.
Самый простой способ – это построить
их векторное произведение
перпендикулярны и прямой, лежащей на
пересечении этих плоскостей. Найдем
вектор
,
который перпендикулярен векторам
и
.
Самый простой способ – это построить
их векторное произведение
 :
:

Отсюда вытекает:
 .
.
Найдем точку , через которую проходит прямая. Очевидно, что эта точка должна лежать на пересечении плоскостей. Поэтому запишем:

Для определения трех неизвестных имеем всего два уравнения. Здесь можно поступить следующим простым способом.
Принять
 и решить систему
и решить систему

Если решение существует, то точка найдена. Иначе, переходим в пункт 2.
Принять
 и решить систему
и решить систему
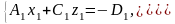
Если решение существует, то точка найдена. Иначе, переходим в пункт 3.
Принять
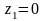 и решить систему
и решить систему

Если решение существует, то точка найдена. Иначе, искомая прямая не существует, например, исходные плоскости не пересекаются.
Из канонического уравнения можно получить параметрическое уравнение прямой, приравнивая каждую дробь в отдельности некоему параметру t. Затем из этих трех равенств выражают координаты (x,y,z) точек описываемой прямой:

