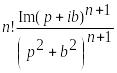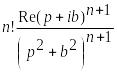- •Часть 2. Дифференциальные уравнения в частных производных первого порядка Лекция 11. Уравнения в частных производных первого порядка
- •11.1. Линейные и квазилинейные уравнения
- •11.2. Уравнения с переменными коэффициентами. Характеристики
- •11.3. Решение задачи Коши
- •12.2. Уравнение колебаний стержня
- •12.3. Уравнение теплопроводности и диффузии
- •12.4. Уравнения гидродинамики и звуковых волн
- •Лекция 13. Классификация уравнений в частных производных 2-го порядка, приведение их к каноническому виду и нахождение общего решения
- •Задания для самостоятельной работы
- •Лекция 14. Начальные и граничные условия
- •14.1. Начальные условия
- •14.2. Краевые задачи
- •Лекция 15. Решение задачи коши для волнового уравнения
- •15.1. Решение задачи Коши методом Даламбера
- •15.2. Решение задачи Коши для волнового уравнения методом Тейлора
- •Задания для самостоятельной работы
- •Лекция 16. Решение граничных задач волнового уравнения
- •16.1. Метод Фурье (метод разделения переменных) для уравнения свободных колебаний струны
- •16.2. Метод Фурье (метод разделения переменных) для уравнения вынужденных колебаний струны
- •Задания для самостоятельной работы
- •Лекция 16 (продолжение). Задача о напряженном состоянии элемента вооружения долота режущего действия
- •Лекция 17. Уравнения теплопроводности (диффузии) и методы их решений
- •17.1. Методы решения задачи Коши
- •Задания для самостоятельной работы
- •17.2. Методы решения граничных задач
- •Лекция 17 (продолжение). Расчет глубины промерзания связанных горных пород
- •Лекция 18. Стационарные уравнения. Уравнение лапласа и методы его решения
- •18.1.Задачи, приводящие к уравнениям эллиптического типа
- •18.2. Решения краевых задач для уравнения Лапласа в круге
- •Задания для самостоятельной работы
- •Лекция 19. Уравнение неразрывности и уравнения эйлера
- •19.1. Гипотеза сплошности
- •19.2. Установившееся и неустановившееся движения.
- •19.3. Уравнения гидродинамики и звуковых волн
- •19.4. Закономерности распространения плоских упругих волн
- •Лекция 20. Закономерности преломления и отражения плоских упругих волн на плоскости контакта твердых тел
- •Часть 4. Преобразование лапласа и его применение при решении дифференциальных уравнений Лекция 21. Преобразование лапласа
- •21.1. Преобразование Лапласа
- •21.2. Основные свойства преобразования Лапласа
- •21.3. Свертка функций
- •21.4. Оригиналы с рациональными изображениями
- •21.5. Нахождение оригинала по заданному изображению (когда оно рационально)
- •21.6. Оригиналы с изображениями, регулярными в бесконечности
- •Лекция 22. Практическое применение преобразования лапласа
- •22.1. Приложения к решению линейных дифференциальных уравнений с постоянными коэффициентами
- •22.2. Использование преобразования Лапласа при решении уравнений в частных производных
- •Лекция 23. Миграционная подмодель радиогеоэкологической модели подземного регионального хранилища радиоактивных отходов и ядерных материалов
- •Вопросы к экзамену по дисциплине: «Дифференциальные уравнения в горном деле»
21.5. Нахождение оригинала по заданному изображению (когда оно рационально)
Предыдущие выкладки показывают, что если - какая-нибудь правильная рациональная дробь, разложение которой на простейшие дроби есть
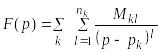
то
![]() (21.20)
(21.20)
будет оригиналом, имеющим изображение .
В частности, если все полюсы - простые, то
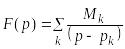 ;
;
![]() ,
,
и для оригинала, имеющего изображение , получим формулу
![]() (21.21)
(21.21)
Заметим еще, что если
![]() (21.22)
(21.22)
то соответствующим оригиналом будет
![]() (21.23)
(21.23)
Таким образом, нахождение оригинала по заданному рациональному изображению сводится к разложению правильной рациональной дроби на простейшие дроби.
Пример 21.1. Найти оригинал , имеющий изображение
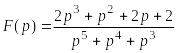 .
.
Разложим это изображение на простейшие дроби:
![]() .
.
Первое слагаемое
в полученном изображении можно умножить
и разделить на 2:
![]() ,
т.к.
,
т.к.
![]() при
при
![]() и
и
![]() .
Учитывая формулу (1.8), запишем оригинал
этого изображения:
.
Учитывая формулу (1.8), запишем оригинал
этого изображения:
![]() ≒
≒![]() .
.
Второе слагаемое
представим в виде:
![]() ,
которое соответствует виду изображения
(21.22) -
,
при
,
которое соответствует виду изображения
(21.22) -
,
при
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Учитывая формулу (21.23), запишем оригинал
этого изображения:
.
Учитывая формулу (21.23), запишем оригинал
этого изображения:
![]() ≒
≒![]() .
.
Таким образом, окончательный вид оригинала, соответствующий исходному изображению, будет:
![]() ≒
.
≒
.
Пример
21.2.
Найти
оригинал
,
имеющий
изображение
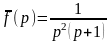 .
.
Рассмотрим два метода.
Разложение изображения на сумму изображений.
Представим исходное изображение в виде суммы простых дробей
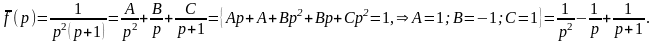
С учетом того, что
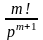 ≒tm,
то при m
= 1, будем иметь
≒tm,
то при m
= 1, будем иметь
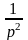 ≒t
и
≒t
и
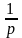 ≒1;
≒1;
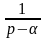 ≒
≒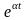 ,
то при α
= -1, будем иметь
,
то при α
= -1, будем иметь
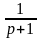 ≒e-t.
≒e-t.
Следовательно, изображение имеет оригинал вида t-1+e-t, т.е.
≒ t-1+e-t.
2. Разложение изображения на произведение изображений.
Обозначим
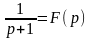 ≒e-t
= f1(t)
и
≒e-t
= f1(t)
и
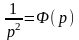 ≒t
= f2(t).
≒t
= f2(t).
Применив формулу Дюамеля ≒ , получим
≒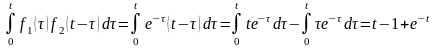
Следовательно, изображение имеет оригинал вида t-1+e-t, т.е.
≒ t-1+e-t.
Пример
21.3.
Найти
оригинал
,
имеющий
изображение
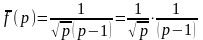 .
.
Обозначим
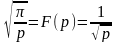 ≒
≒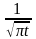 = f1(t)
и
= f1(t)
и
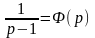 ≒
et
= f2(t).
≒
et
= f2(t).
Применив формулу Дюамеля ≒ , получим
≒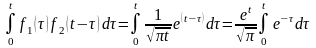
Следовательно,
изображение
имеет оригинал вида
 ,
т.е.
,
т.е.
≒ .
21.6. Оригиналы с изображениями, регулярными в бесконечности
1. Для изображения регулярного в бесконечности.
Для того чтобы изображение было регулярно в бесконечно удаленной точке, необходимо и достаточно, чтобы оригинал являлся целой функцией экспоненциального типа.
Определим понятие
целой функцией
экспоненциального типа.
Итак, целая функция
![]() комплекснозначного переменного
комплекснозначного переменного
![]() называется целой
функцией экспоненциального типа,
если можно найти такие положительные
числа
называется целой
функцией экспоненциального типа,
если можно найти такие положительные
числа
![]() и
и
![]() ,
чтобы для всех комплексных значений
выполняется неравенство
,
чтобы для всех комплексных значений
выполняется неравенство
![]() .
(21.24)
.
(21.24)
Существует также лемма, которая доказывает, что для того чтобы степенной ряд
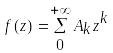 ,
(21.25)
,
(21.25)
изображал целую
функцию экспоненциального типа,
необходимо и достаточно, чтобы для
некоторых чисел
и
![]() выполнялись неравенства
выполнялись неравенства
![]() .
(21.26)
.
(21.26)
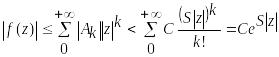 ,
,
Необходимо отметить, что операции линейного комбинирования, умножения на независимое переменное, умножения на показательную функцию, линейного преобразования независимого переменного, дифференцирования и интегрирования, примененные к целым функциям экспоненциального типа, приводят снова к целым функциям экспоненциального типа.
Приведенная лемма позволяет реализовать доказательную базу приведенного выше утверждения о том, что для того чтобы изображение было регулярно в бесконечно удаленной точке, необходимо и достаточно, чтобы оригинал являлся целой функцией экспоненциального типа.
Необходимо отметить, что всякая регулярная в бесконечности аналитическая функция, равная нулю в бесконечности, является изображением некоторой целой функции экспоненциального типа. Из этого замечания заключаем, что с помощью преобразования Лапласа устанавливается взаимно однозначное соответствие между всеми целыми функциями экспоненциального типа и всеми аналитическими функциями, регулярными в бесконечно удаленной точке и равными в ней нулю.
2. Нахождение оригинала по его изображению (когда оно регулярно в бесконечности).
Предыдущим
изложением показано, что если
– какая-нибудь аналитическая функция,
регулярная в бесконечно удаленной точке
и равная в ней нулю, и если ее разложение
в виде
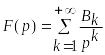 ряда Лорана в окрестности бесконечности,
то выражение
ряда Лорана в окрестности бесконечности,
то выражение
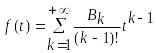 (21.27)
(21.27)
будет оригиналом, имеющим изображение вида - .
3. Изображение бесселевых функций.
Функция
Бесселя 1-го рода
-го
порядка, являющаяся первым частным
решением уравнения Бесселя при
![]() имеет вид:
имеет вид:

или
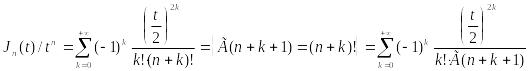 .
.
Следовательно,
можно утверждать, что функция
![]() является целой функцией экспоненциального
типа вида -
является целой функцией экспоненциального
типа вида -
 ,
у которой
,
у которой
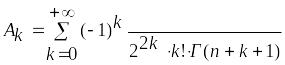 .
Таким образом, изображение этой функции
определяется формулой (1.29) -
.
Таким образом, изображение этой функции
определяется формулой (1.29) -
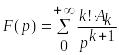 .
Поэтому изображение будет иметь вид:
.
Поэтому изображение будет иметь вид:
![]() ,
и окончательно получим
,
и окончательно получим
≒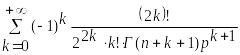 .
.
При
![]() получим
получим
![]() ≒
≒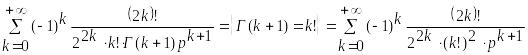
С другой стороны, биномиальное разложение правой части приводит изображение к виду
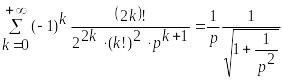 ,
,
следовательно, получим
≒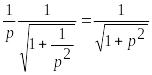 .
.
Используя метод индукции можно записать изображение бесселевой функции при любом положительном n:
![]() ≒
≒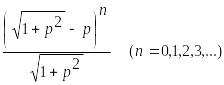 (21.28)
(21.28)
Если изображение
имеет вид
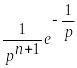 ,
то этому изображению соответствует
оригинал вида:
,
то этому изображению соответствует
оригинал вида:
![]() ≒
(21.29)
≒
(21.29)
и при
![]() ≒
≒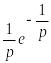 .
.
В таблице 21.1 приведены наиболее часто встречающиеся оригиналы функций и соответствующие им изображения.
Таблица 21.1.
|
Оригинал – |
Изображение – |
1 |
2 |
3 |
1. |
( |
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
tnsin bt |
|
9. |
|
|
10. |
|
|
11. |
|
|
|
|
Продолжение табл.21.1 |
1 |
2 |
3 |
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
|
17. |
|
|
18. |
|
|
19. |
|
|
20. |
|
|
21. |
|
|
22. |
|
|
23. |
|
|
24. |
|
|
25. |
|
|
|
|
Продолжение табл. 21.1 |
1 |
2 |
3 |
26. |
|
|
27. |
|
|