1. Определение Множества. Элементы. Пустое, универсальное, подмножество. Равенства подмножеств. Множествами и их свойства. Декартово произведение множеств.

Множество – это совокупность объектов, рассматриваемых как единое целое.

Элементы:a,b,c,a₂,b₃

Способы задания множеств:

1. Перечисление элементов: М={0,1,2,…,9}

2. Указание свойств Р(х), которым элементы множества должны удовлетворять: М={x | P(x)}.

Множество А называется подмножеством множества В, если все элементы А принадлежат В, т.е.

Множества А и В называются равными или совпадающими, если они состоят из одних и тех же элементов, т.е.

Множество, не содержащее ни одного элемента называется пустым ø.

Множество, содержащее все элементы, находящиеся в рассмотрении, называется универсальным или универсумом U.

Свойства основных операций над множествами:

1. Ассоциативность:

2. Коммутативность:

3. Идемпотентность:

4. Дистрибутивность:

5. Поглощение:

6. Законы де Моргана:

7. Законы нуля и единицы: 0=ø, 1=U

8. Закон двойного отрицания:

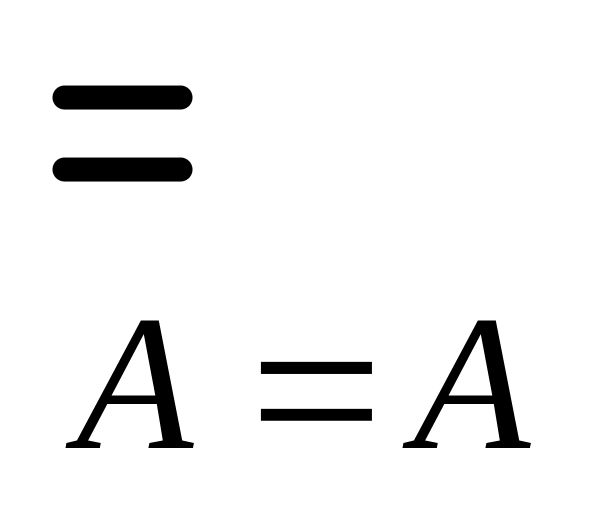
3.Упорядоченную последовательность (х₁, х₂,…,х_n) называют кортежем длины n.

Декартовым(прямым) произведением множеств А₁, А₂,…, А_n называется множество {(x₁, x₂,…, x_n) | x₁ є A₁,…, x_n є A_n}.

Если А₁=А₂=…=А_n, то – n-ная декартова степень множества А.

А⁰ = ø

2. Операции над множествами. Диаграммы Венна.

1) объединение

2 ) пересечение

3) вычитание

4) кольцевая сумма (симметрическая разность)

5) дополнение

4. Отношения. Унарные и бинарные, Тождественное и универсальное.

n-местным отношением(или n-местным предикатом)Р на множествах А₁, А₂,…, А_n называется любое подмножество прямого произведения . Элементы х₁, х₂,…, х_n (где х_i є A_i) связаны соотношением Р тогда и только тогда, когда (х₁, х₂,…, х_n) є Р. При n=1 отношение Р является подмножеством множества А₁ и называется унарным отношением или свойством.

При n=2 отношение Р называется бинарным отношением или соответствием.

U = A² – универсальное отношение.

5. Отношения. Область определения, значений. Обратное отношение.

Пусть Р – некоторое бинарное отношение. Областью определения отношения Р называется множество δ_Р = {x | (x,y) є P для некоторого у}. Областью значений отношения Р называют множество ρ_Р = {y | (x,y)єP для некторого х}. Обратным отношением называется множество Р^-1 = {(y,x) | (x,y) є P}.

Образом множества Х относительно предиката Р называется множество Р(Х)={y | (x,y) є P для некоторого х є Х}

Прообразом множества относительно предиката Р называется множество Р^-1(Х) или, другими словами, образ множества Х относительно предиката Р^-1.

Произведением бинарных отношений и или композицией Р₁ и Р₂ называется множество Р₁•Р₂ = {(x,y) | x є A, y є C, и найдется элемент z є B такой, что (x,z) є Р₁ и (z,y) є P₂}.

Свойства:

1. Ассоциативность композиции: (P•Q)•R=P•(Q•R)

Доказательство: Пусть (x,y) є (P•Q)•R. Тогда для некоторых u и v имеем (x,u) є P, (u,v) є Q, (v,y) є R. Тогда (u,y) є Q•R и (x,y) є P•(Q•R). Включение P•(Q•R) є (P•Q)•R доказывается аналогично.

2. (P•Q)^-1=Q^-1•P^-1

Доказательство: Предположим, что (x,y) є (P•Q)^-1. Тогда (y,x) є P•Q, и, следовательно, (y,z) є P и (z,x) є Q для некоторого элемента z. Значит (x,z) є Q^-1, (z,y) є P^-1 и тогда (x,y) є Q^-1•P^-1. Обратное включение доказывается аналогично.

3. P•Q ≠ Q•P

4. (P^-1)^-1=P

Доказательство: Если (x,y) є P, то (y,x) є Р^-1, но тогда (x,y) є (Р^-1)^-1.