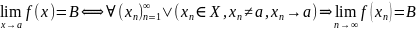- •3. Свойства действительных чисел. Важнейшие подмножества .
- •4. Ограниченные и неограниченные числовые множества. Грани числовых мно-
- •5. Предел числовой последовательности.
- •6. Свойства предела числовой последовательности.
- •7. Предел последовательности и неравенства.
- •9. Предельный переход и арифметические операции над последовательностями.
- •10. Монотонные последовательности. Число е.
- •11.Сравнение асимптотического поведения последовательностей
- •13.Лемма о вложенных отрезках.
- •14.Фундаментальные последовательности.
- •15.Нижний и верхний пределы последовательности.
- •16. Отображения и их основные типы. Функция действительной переменной.
- •17. Основные классы функций.
- •18. Предел функции. Определения Гейне и Коши.
- •19. Односторонние пределы. Эквивалентность определений предела Гейне и Коши.
- •20. Общие свойства предела функции. Арифметические операции и предельный пе-реход. Предельный переход и неравенства.
- •21. Бесконечно малые и бесконечно большие функции.
- •26. Критерий Коши для функций.
- •27. Непрерывность функции. Точки разрыва и их классификация. Односторонняя и кусочная непрерывность.
- •28.Локальные свойства непрерывных функций.
- •29.Глобальные свойства непрерывных функций. Теорема Больцано-Коши.
- •30.Глобальные свойства непрерывных функций. Теоремы Вейерштрасса.
- •31) Теорема о существовании и непрерывности обратной функции
- •32) Равномерная непрерывность. Теорема кантора
- •33) Непрерывность элементарных функций
- •34. Дифференцируемые функции. Определение производной функции в точке. Условия дифференцируемости функции в точке.
- •36. Односторонние и бесконечные производные.
- •43.Производные и дифференциалы высших порядков. Формула Лейбница. Неинва-
- •44. Локальная формула Тейлора. Единственность многочлена Тейлора.
- •45. Представление остаточного члена в формуле Тейлора в формах Лагранжа и Коши.
- •46. Разложение по ф-ле Маклорона важн элемент ф-ий
- •47. Многочлен Тейлора как многочлен наилучшего приближения функции в окрестности данной точки.
- •50 Выпуклость графиков функции.
- •51. Точки перегиба.
- •52 Асимптоты графика функции.
- •52(Продолжение)
17. Основные классы функций.
Обратимые:
Df
Числовая ф-ция y=f(x)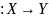 наз обратимой
на мн-ве Х, если она осуществляет биекцию
наз обратимой
на мн-ве Х, если она осуществляет биекцию
Прямая
y=y0:
y0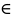 Y
пересекает график ф-ции в одной точке
Y
пересекает график ф-ции в одной точке
Для обратимых ф-ций и только для них сущ обратные ф-ции
Df
Пусть ф-ция y=f(x)
- обратимая на Х, тогда обратной
ф-цией наз x=f-1(y) ,
что f
,
что f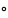 f-1=f(f-1(y))=y
и f-1
f=f-1(f(x))=x
f-1=f(f-1(y))=y
и f-1
f=f-1(f(x))=x
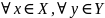
Nt Если f-1 – обратная ф-ция для f , то f – обратная для f-1
Th График обратной ф-ции симметричен графику исходной ф-ции относительно прямой y=x
Монотонные:
Df Пусть
f наз возрастающей, если
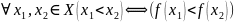
f наз неубывающей, если
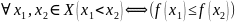
f наз убывающей, если
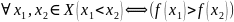
f наз невозрастающей, если
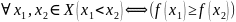
Если ф-ция f удовлетворяет 2) или 4), ее называют монотонной
Если ф-ция f удовлетворяет 1) или 3), ее называют строго монотонной
Th
Каждая строго монотонная ф-ция
 имеет единственную
имеет единственную
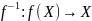
Док-во:
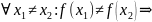 f
– инъективна
f
– инъективна
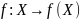 – сюрьективна
– сюрьективна
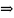 f
– биекция
f
– биекция
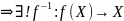
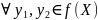 пусть y1=f(x1),
y2=f(x2)
пусть y1=f(x1),
y2=f(x2)
Пусть
f
возрастающая
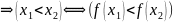
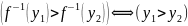
Аналогично при f – убывающей
Четные:
Df Пусть область определения симметрична относительно 0. Тогда f наз
а)
четной,
если
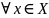 :
f(-x)=f(x)
:
f(-x)=f(x)
б) нечетной, если : f(-x)=-f(x)
Любую ф-цию, область определения которой симметрична отн 0, можно представить в виде суммы четной и нечетной
График четной ф-ции симметричен относительно оси ординат (y), нечетной – относительно начала координат
Периодические:
Df
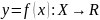 наз периодической,
если
наз периодической,
если
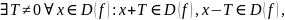 f(x)=f(x+T)=f(x-T)
f(x)=f(x+T)=f(x-T)
T наз периодом ф-ции
Свойства периодических ф-ций:
Область определения периодической ф-ции не может быть ограниченной
Если Т – период f, то любое число вида kT (
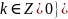 )
также является периодом
)
также является периодом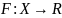 - периодическая,
если
- периодическая,
если
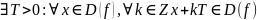
У любой периодической ф-ции есть положительный период
Df Если у периодической ф-ции существует наименьший положительный периода, то он называется основным периодом ф-ции
18. Предел функции. Определения Гейне и Коши.
Классификация точек множества:
Df
Элемент а
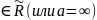 называется предельной
точкой мн-ва
называется предельной
точкой мн-ва
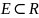 ,
если в любой его проколотой окрестности
Ů(а)
содержится бесконечно много точек из
Е
,
если в любой его проколотой окрестности
Ů(а)
содержится бесконечно много точек из
Е
Df
Точка а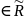 ( или а
= ∞ ) наз изолированной
точкой мн-ва
Е, если а
Е
и а
не является предельной точкой для Е
(если
( или а
= ∞ ) наз изолированной
точкой мн-ва
Е, если а
Е
и а
не является предельной точкой для Е
(если
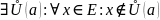 )
)
Df Точка а ( или а = ∞ ) наз внутренней точкой мн-ва, если она содержится в Е вместе некоторой своей окрестностью.
Предел ф-ции:
Df (по Коши в терминах окрестностей)
Пусть
, и точка а
( или а
= ∞ ) – предельная точка Х. Принято
говорить, что элемент В
(или В = ∞ ) является пределом
функции f
при
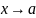 по множеству Х,
если
по множеству Х,
если


Nt
Если а – изолированная точка мн-ва Х, то говорить о пределе в этой точке нельзя
Если ф-ция f имеет предел
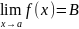 ,
то она имеет тот же самый предел и по
любому подмножеству Е
,
то она имеет тот же самый предел и по
любому подмножеству Е Х,
если а
– предельная точка Е
Х,
если а
– предельная точка Е
Df (в терминах «ε-δ»)
Пусть и а – предельная точка мн-ва Х, тогда

Пусть
 или
или
 - предельная точка мн-ва Х
- предельная точка мн-ва Х
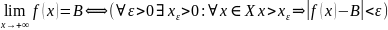
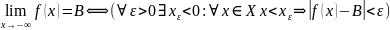
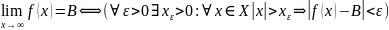
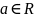 - предельная точка мн-ва Х
- предельная точка мн-ва Х
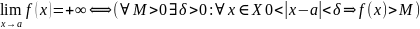
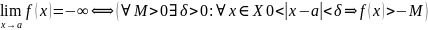
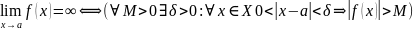
Df (по Гейне)
Пусть
а
или а
= ∞ . Тогда В
или В = ∞ является пределом
функции f
при
по множеству Х,
если
 соответствует последовательность
значений
соответствует последовательность
значений