
- •3. Умножение матриц. Свойства.
- •4. Транспонирование матриц. Свойства.
- •5. Перестановки.
- •6. Понятие определителя.
- •7. Частные случаи определителей.
- •8. Свойства определителя.
- •9. Миноры и алгебраические дополнения.
- •10. Теоремы о разложениях определителя
- •11. Обратная матрица
- •1. Матрицы. Основные определения.
- •2. Линейные операции над матрицами и их свойства.
- •21. Понятие базиса. Координаты.
- •22. Декартова прямоугольная система координат.
- •24. Выражение для скалярного произведения в декартовых координатах.
- •23. Скалярное произведение двух векторов. Его физический смысл. Геометрические и алгебраические свойства.
- •26. Выражение для векторного произведения в декартовых координатах.
- •25. Векторное произведение. Его свойства.
- •29. Уравнение плоскости и прямой на плоскости в отрезках.
- •27. Смешанное произведение трёх векторов. Его свойства и выражение в декартовых координатах.
- •36. Гипербола и ее св-ва.
- •37. Понятие о поверхностях 2го порядка.
- •28. Общее уравнение плоскости и прямой на плоскости.
- •40. Функции и её предел.
- •35. Эллипс.
- •34.Парабола. Определение. Вывод канонического уравнения.
- •30. Нормальное ур-е пл-ти и прямой на пл-ти
- •31.Уравнения прямой, проходящей через заданную точку параллельно заданному вектору.
- •32. Канонические уравнения прямой.
- •33. Уравнение прямой на плоскости с угловым коэффициентом.
- •42.Основные теоремы о пределах
- •43.Первый замечательный предел
- •44.Второй замечательный предел
- •45.Непрерывность ф-циив точке
- •48. Некоторые свойсва непрерывной ф-ции
- •46. Классификация точек разрыва
- •50. Производная. Определение и физ. Смысл.
- •49, Сравнение бесконечно малых
- •51. Геометрический смысл производной
- •54. Обратная функция и её диффренциирование
- •55.Обратные тригонометрические функции и их производные
- •12. Ранг матрицы.
- •53. Производная сложной функции:
- •56.Производные от функций и
- •57. Гиперболические функции
- •13. Линейные системы уравнений. Основные определения. Матричная запись.
- •14. Формула Крамера
- •15. Метод Гаусса
- •16. Решение произвольных систем уравнений
- •17. Однородные системы уравнений.
- •19. Линейные операции над векторами
- •20. Линейнонезависимые системы векторов.
- •38. Действительные числа, переменные велечины
- •39. Предел переменной величины.
- •41. Бесконечно малые и бесконечно большие.Теоремы.
- •47. Непрерывность функции вна интервали и на отрезке
- •58. Таблица производных
- •52. Основные правила дифференцирования.
54. Обратная функция и её диффренциирование
Пусть
дана монотонная функция y=f(x)
(монотонно возрастающая или монотонно
убывающая). Для примера рассмотрим
монотонно возрастающую.Тогда различным
значениям аргумента
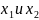 соответствуют различные значения
функции: y=f(
соответствуют различные значения
функции: y=f(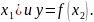
Т.е. для монотонной функции существует взаимно однозначное соответствие между значениями х и y.
Каждому значению y соответствует единственное соответствие х и в данном случае формально можно считать, то переменная х является функцией от y.
X=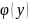
Эта функция X= называется обратной по отношению к функции y=f(x) .
Теорема:
Если
для функции y=f(x)
существует обратная функция
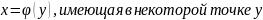 производную
производную
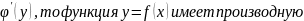 в соответствующей точке
в соответствующей точке
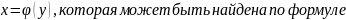
 ’(X)=
’(X)=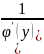
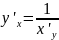
Доказательство:
Дадим
приращение
 тогда
переменная х получит приращение
тогда
переменная х получит приращение
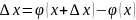
Причём
в силу монотонности f(x)
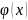
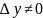 ,
то ∆х≠0.
,
то ∆х≠0.
Т.к.
в этом случае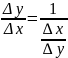 .
.
Перейдём
в обеих частях этого равенства к пределу
∆х→0,
тогда
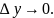
Тогда
имеем
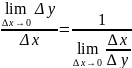 ⇒
⇒ =
=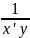 .
.
55.Обратные тригонометрические функции и их производные
Функция y=sin x монотонно возрастающая на отрезке [-π;π]
Пусть y=arcsin x
X=sin y
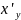 =cos
y
=cos
y
= =
=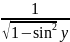 =
=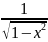
(arcsin x)’=
Аналогично
можно ввести функцию y=cos
x
[0;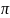 ]
]
Рассуждая
можно показать, что

Y=tg
x
при x и изменяется на отрезки (-
и изменяется на отрезки (- образованная функция, которая обозначается
y=arctg
x
(-
образованная функция, которая обозначается
y=arctg
x
(-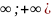
(arctg
x)’=
Y=arctg x –отрицательна по отношению к функции
Y=ctg
x
имеет производную, определённую
формулой
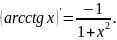
12. Ранг матрицы.
Рангом матрицы называется наибольший порядок её миноров, отличных от нуля.
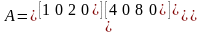
Миноры 3 порядка этой матрицы = 0, т. к. они содержат нулевой столбец.
rA≤2. Все миноры 2 порядка будут содержать либо нулевой столбец, либо 2 пропорциональных столбца, и => тоже все = 0.
rA=1. Т. к. у этой матрицы есть миноры первого порядка, отличные от 0, то её ранг = 1.
Элементарные преобразования матрицы:
1. умножение любого ряда матрицы на число, отличное от нуля.
2. прибавление к элемента одного ряда матрицы элементов другого её параллельного ряда, умноженных на некоторое число.
3. перемена мест любых 2-х рядов матрицы.
Теорема. Ранг матрицы, полученной из данной путём элементарных преобразований, равен рангу данной матрицы.
Метод окаймляющих миноров нахождения рангов матрицы.
Пусть М – минор порядка k матріцы А. Окаймляющим его минором называется минор порядка k+1 этой матрицы, содержащий внутри себя минор М.
Теорема. Если матрица А имеет минор М порядка k, отличный от нуля, и все миноры, окаймляющие этот минор М, равны нулю, то ранг матрицы А=k.
Метод окаймляющих миноров нахождения ранга состоит в следующем: находят минор данной матрицы, отличный от 0 (1 или 2 порядка), затем вычисляют все окаймляющие миноры. Если они все = 0, то ранг матрицы = порядку этого ненулевого минора. Если среди окаймляющих находится один, отличный от нуля, то далее вычисляют все миноры, окаймляющие данный минор, у которых все окаймляющие миноры = 0. Ранг матрицы будет = порядку этого ненулевого минора.
