Замечание: Иногда в литературе под ф-ей Лапласа подразумевается др. Ф-ия в этом случае интегральная ф-ла Лапласа

17. Двумерные случайные величины

Упорядоченная пара (X, У) случайных величин X и У называется двумерной случайной величиной, или случайным вектором двумерного пространства.

Двумерная случайная величина (X, У) называется также системой случайных одномерных величин X и У.

Множество всех возможных значений дискретной двумерной слу­чайной величины с их вероятностями называется законом распределения этой случайной величины.

Условное математическое ожидание - дискрет. СВ Y при условии Х=х наз. M(Y / {X=x)=E yj*p(yj / x).

Функция регрессии : M(Y/X=x)=M(Y/x)=ф(y)

15. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение и моменты дискретной случайной величины.

Теорема. Для любой СВ математическое ожидание ее отклонения равно нулю, т.е.

.Дисперсией (рассеянием) СВ наз математическое ожидание квадрата отклонения этой величины от ее математического ожидания:

.

Очевидно, что дисперсия СВ постоянна, т.е. явл числовой характеристикой этой величины.

Св-ва дисперсии:

Теорема. Дисперсия постоянной величины равна нулю.

Теорема. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат .

Теорема. Дисперсия СВ = разности математического ожидания ее квадрата и квадрата математического ожидания самой величины: .

Теорема. Дисперсия суммы двух независимых СВ равна сумме дисперсий этих величин:

.

Следствие 1. Дисперсия суммы нескольких взаимно независимых СВ = сумме дисперсий этих величин.

Следствие 2. Если – постоянная величина, то .

Следствие 3. Дисперсия разности двух независимых СВ = сумме дисперсий этих величин, т.е. если СВ и независимы, то .

Средним квадратичным отклонением (или стандартом) СВ называется корень квадратный из дисперсии этой величины: .

21. Распределение Бернулли и его числовые характеристики. Случайная величина X имеет распределение Бернулли, если она равна количеству наступлений события А в серии из п независимых испытаний, проводимых по схеме Бернулли. Возможными значениями это случайной величины являются числа Вероятность того, что данная случайная величина примет значение, равное т, может быть вычислена по формуле Бернулли

Числовые характеристики случайной величины, имеющей распределение Бернулли:

Примером случайной величины, имеющей распределение Бернулли является случайная величина, равная числу попаданий в серии из п выстрелов.

22. Биномиальный закон распределения и его числовые характеристики. Биномиальное распределение описывает повторяющиеся независимые опыты. Этот закон определяет появление события раз при независимых испытаниях, если вероятность появления события в каждом из этих опытов не изменяется от опыта к опыту. Вероятность: ,

где: – известная вероятность появления события в опыте, не изменяющаяся от опыта к опыту;

– вероятность непоявления события в опыте;

– заданное число появления события в опытах;

– число сочетаний из элементов по .

В25. Вырожденное распределение и гипергеометрическое распределение. Гипергеометри́ческое распределе́ние в теории вероятностей моделирует количество удачных выборок без возвращения из конечной совокупности.

Гипергеометрическое распределение описывает вероятность того, что в выборке из n различных объектов, вытянутых из поставки ровно k объектов являются бракованными.

В общем, если случайная величина X соответствует гипергеометрическому распределению с параметрами N, D и n, то вероятность получения ровно k успехов определяется формулой

:

26. Равномерный закон распределения, графики функции и плотности распределения, числовые характеристики. Непрерывная случайная величина считается равномерно распределенной, если ее плотность вероятности имеет вид:

Характеристики:

1. Математическое ожидание:

2. Моды равномерное распределение не имеет.

3. Дисперсия может быть вычислена следующим образом:

Среднее квадратичное отклонение будет иметь вид:

.

29. Связь стандартного нормального распределения с нормальным распределением. Вероятность попадания нормально распределенной случайной величины в заданный интервал. Во многих практических задачах требуется определить вероятность попадания случайной величины в заданный интервал. Эта вероятность может быть выражена в виде разности функции распределения вероятности в граничных точках этого интервала

Следовательно, искомая вероятность может быть выражена через веденный ранее стандартный интеграл Лапласа:

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Функция Z распределения (или стандартное нормальное) определяется следующей формулой:

f(x) = 1/[(2p)^1/2] * e**{-1/2*x²}

-∞ < x < ∞

Нормальным называется такое распределение случайной величины , плотность вероятности которого описывается функцией Гаусса:

где – среднее квадратичное отклонение; – математическое ожидание случайной величины.

44. Выборочные ковариация и коэффициент корреляции. Линейная регрессия. Для определения значений теоретических коэффициентов, входящих в уравнения регрессии необходимо знать и использовать все значения переменных генеральной совокупности, что практически невозможно. В связи с этим по выборке ограниченного объема строится так называемое выборочное (эмпирическое) уравнение регрессии. В силу несовпадения статистической базы для генеральной совокупности и выборки оценки коэффициентов, входящих в уравнение регрессии, практически всегда отличаются от истинных (теоретических) значений, что приводит к несовпадению эмпирической и теоретической линий регрессии. Различные выборки из одной и той же генеральной совокупности обычно приводят к отличающимся друг от друга оценкам. Задача состоит в том, чтобы по конкретной выборке найти оценки неизвестных параметров так, чтобы построенная линия регрессии являлась бы наилучшей, среди всех других линий.Если функция регрессии линейна, то говорят о линейной регрессии. Линейная регрессия (линейное уравнение) является наиболее распространенным (и простым) видом зависимости между экономическими переменными. Для этого простейшего случая имеем:

или

Последнее соотношение называется теоретической линейной регрессионной моделью; коэффициенты – теоретическими параметрами регрессии; – случайным отклонением.

30. Параметры нормального распределения и их вероятностный смысл. Влияние параметров нормального распределения на форму нормальной кривой. Асимметрия и эксцесс распределения случайной величины. Нормальное распределение определяется двумя параметрами: а и σ. Достаточно знать эти пара­метры, чтобы задать нормальное распределение. Вероятностный смысл этих параметров таков: а есть математическое ожидание, σ — среднее квадратическое отклонение нормального распределения.

Влияние параметров нормального распределения на форму нормальной кривой. Известно, что графики функций f(х) и f(x—а) имеют одинаковую форму; сдвинув график f (х) в положитель­ном направлении оси х на а единиц масштаба при а > О или в отрицательном направ­лении при а < 0, получим график f(x—а). Отсюда сле­дует, что изменение величины параметра а (математиче­ского ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если а возрастает, и влево, если а убывает.

По-иному обстоит дело, если изменяется параметр σ: с возрастанием σ максимальная орди­ната нормальной кривой убывает, а сама кривая стано­вится более пологой, т. е. сжимается к оси Ох; при убывании σ нормальная кривая становится более «остро-вершинной» и растягивается в положительном направле­нии оси Оу.

Асимметрией распределения случайной величины называется отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения:

.

Эксцессом распределения случайной величины называют число, определяемое выражением:

.

Для нормального распределения , поэтому эксцесс равен нулю.

19. Коэффициент корреляции случайных величин(с.в.) и его свойства. Коэффициент корреляции с.в. и наз. число

.

Св-ва коэффициента корреляции: 1) r(X,Y)= r(Y,X); 2) r(X,X)=1; 3) , при этом r(X,Y)= ±1 тогда и только тогда, когда Y=aX+b, где a и b- некоторые постоянные; 4) r(aX+b, cY+ d)= sign(ac)*r(X,Y), где a,b,c,d-постоянные, а sign x= x/|x|-функция знака; 5) если X и Y независимы , то r(X,Y)=0.

31. Правило трех сигм нормально распределенной случайной величины, смысл и значение для практики.

Сущность правила «трех сигм»: Если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратичного отклонения.

На практике правило «трех сигм» применяют так: если распределение изучаемой средней величины неизвестно, но правило «трех сигм» выполняется, то есть основания полагать, что изучаемая величина распределена нормально, и наоборот.

37. Предмет и задачи математической статистики. Генеральная и выборочная совокупности. Способ отбора. Математическая статистика – наука о математических методах систематизации и использования статистических данных для научных и практических выводов, опирающаяся на теорию вероятностей.

Объектами изучения математической статистики являются случайные события, величины и функции, которые характеризуют рассматриваемое случайное явление. Случайными являются следующие события: выигрыш на один билет денежной лотереи, соответствие контролируемого продукта установленным требованиям, безотказная работа автомобиля в течение первого месяца его эксплуатации, выполнение подрядчиком суточного графика работ.

Выборочной совокупностью называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Способы отбора: 1 Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся а) простой случайный бесповторный отбор и б) простой случайный повторный отбор. 2) Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся а) типический отбор, б) механический отбор и в) серийный отбор.

Простым случайным называют отбор, при котором объекты извлекаются по одному из генеральной совокупности.

Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части.

Механическим называют отбор, при котором генеральная совокупность механически делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы выбирается один объект.

Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию.

42. Основные понятия статистической проверки гипотез. Основная и конкурирующая гипотезы, критерий проверки, ошибки первого и второго рода.

Статистической гипотезой называется всякое высказывание о генеральной совокупности, проверяемое по выборке. Процесс использования выборки для проверки гипотезы называется статистическим доказательством. Основную выдвигаемую гипотезу называют нулевой Н_о. Наряду с нулевой гипотезой рассматривают альтернативную ей Н₁. Выбор между гипотезами Н_о и Н₁ может сопровождаться ошибками двух родов. Ошибка первого рода α означает вероятность принятия Н₁, если верна гипотеза Н₀: α=р(Н₁/ Н₀). Ошибка второго рода означает вероятность принятия Н₀, если верна гипотеза Н₁: β=р(Н₀/Н₁). Существует правильное решение двух видов: р(Н₀/ Н₀)=1-α и р(Н₁/ Н₁)=1-β. Правило, по которому принимают решение о том, верна или не верна гипотеза Н₀, называется критерием, где: α= р(Н₁/ Н₀) –уровень значимости критерия; М=1-β= р(Н₁/ Н₁) –мощность критерия. Статистическим критерием К называют случайную величину, с помощью которой принимают решение о принятии или отклонении Н₀

38. Статистический и вариационный ряд. Эмпирическая функция распределения и ее свойства. Вариационный ряд для дискретных и непрерывных случайных величин. Пусть из генеральной совокупности извлечена выборка, причем значение исследуемого параметра наблюдалось раз, - раз и т.д. При этом объем выборки. Наблюдаемые значения называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом. Числа наблюдений называют частотами, а их отношения к объему выборки - относительными частотами. Вариационный ряд можно представить таблицей вида:

X			…..
n			….

Статистическим распределением выборки называют перечень вариант и соответствующих им относительных частот. Статистическое распределение можно представить как:

X			…..
w			….

где относительные частоты .

Эмпирической функцией распределения называют функцию , определяющую для каждого значения x относительную частоту события X<x. Таким образом, по определению , где – число вариант, меньших x, n – объем выборки.

Свойства эмпирической функции распределения: 1) Значения эмпирической функции принадлежат отрезку [0,1]. 2) – неубывающая функция. 3) Если – наименьшая варианта, то =0 при , если – наибольшая варианта, то =1 при .

Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

32. Функция Лапласа и ее связь с функцией распределения нормальной случайной величины. Свойства функции Лапласа. Для вычисления функции Лапласа используются специальные таблицы или методы приближенного вычисления. Функция обладает следующими свойствами: 1) ; 2) ; 3) функция – нечетная, т.е. = – , поэтому в таблицах обычно приводятся значения только для положительных ; 4) функция – монотонно возрастающая функция (это следует из того, что ). При , с точностью до тысячных можно принять_.

41. Доверительные интервалы для неизвестного математического ожидания и неизвестной дисперсии. Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение  этого распределения известно. Требуется оценить неизвестное математическое ожидание a по выборочному среднему . Найдем доверительные интервалы, покрывающие параметр a с надежностью .Будем рассматривать выборочное среднее _, как случайную величину (т.к. меняется от выборки к выборке), и выборочные значения , как одинаково распределенные независимые случайные величины (эти числа также меняются от выборки к выборке). Другими словами, математическое ожидание каждой из этих величин равно a и среднее квадратическое отклонение – . Так как случайная величина X распределена нормально, то и выборочное среднее также распределено нормально. Параметры распределения равны:

.

Потребуем, чтобы выполнялось соотношение , где – заданная надежность.

Используем формулу .

Заменим X на и  на и получим:

,

где .

Выразив из последнего равенства , получим:

.

Так как вероятность P задана и равна , окончательно имеем:

.

Смысл полученного соотношения – с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр a, причем точность оценки равна .

Таким образом, задача решена. Число определяется из равенства ; по таблице функции Лапласа находят аргумент , которому соответствует значение функции Лапласа, равное .Следует отметить два момента: 1) при возрастании объема выборки n число убывает и, следовательно, точность оценки увеличивается, 2) увеличение надежности оценки приводит к увеличению (так как функция Лапласа – возрастающая функция) и, следовательно, к возрастанию , то есть увеличение надежности оценки влечет за собой уменьшение ее точности.

Если требуется оценить математическое ожидание с наперед заданной точностью и надежностью , то минимальный объем выборки, который обеспечит эту точность, находят по формуле , следующей из равенства .

.

24. Распределение Пуассона и его числовые характеристики. Рассмотрим второй случай асимптотического приближения биномиального распределения, когда , а – имеет конечное значение. Случайная величина называется распределенной по закону Пуассона с параметром , если эта случайная величина может принимать значения , соответствующая вероятность которых определяется по формуле Пуассона, когда :

.

В биномиальном распределении величина имеет смысл математического ожидания. Проведем вычисления математического ожидания для распределения Пуассона:

.

Таким образом, в распределении Пуассона величина также имеет смысл математического ожидания.

Проведем вычисления дисперсии для распределения Пуассона:

,

поскольку

,

Таким образом, в распределении Пуассона дисперсия также равна .

43. Критерий согласия Пирсона (χ² -критерий). Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Имеется несколько критериев согласия, наиболее часто используемым является критерий согласия К. Пирсона («хи квадрат»). Ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.

Пусть по выборке объема n получено эмпирическое распределение:

Варианты……………………

_{Эмпирические частоты…….}

Чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия, и, следовательно, он характеризует близость эмпирического и теоретического распределений.

Доказано, что при n закон распределения случайной величины (А) стремится к закону распределения с степенями свободы независимо от того, какому закону распределения подчинена генеральная совокупность. Поэтому сам критерий называют критерием согласия .

7.Общее пределение вероятности.Свойства вероятностей.Формула сложении явероятностей.

Под вероятностью события понимается некоторая числовая характеристика возможности наступления этого события. Существует несколько подходов к определению вероятности. Основные из них: статистическая вероятность, классическое определение вероятности, геометрическая вероятность.

Статистическая вероятность.Пусть при проведении n испытаний некоторое событие A появилось m раз. Многочисленные эксперименты такого рода показывают, что при больших n отношение m/n, называемое частостью события А, остается примерно постоянным. Статистическое определение вероятности заключается в том, что за вероятность события А принимается постоянная величина, вокруг которой колеблются значения частостей при неограниченном возрастании числа n.

Классическое определение вероятности.Классической вероятностью события А называется отношение числа m элементарных событий, благоприятствующих событию А, к числу n всех злементарных событий из этой схемы:

Р(А)= .

Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости и т.д.). Если геометрическая мера всей области Ω равна mes Ω, а мера части этой области А, попадание в которую благоприятствует данному событию, есть mes А, то вероятность события А определяется по формуле

P(A)=

Свойства вероятностей:

1. P(Ω)=1

2. P(Ø)=0

3. A<B P(A)≤P(B)

4. 0≤P(A)≤1

5. P(Ã)=1-P(A)

Формула сложения вероятности P(A+B)=P(A)+P(B)-P(A*B)

20. Линейная регрессия. Метод наименьших квадратов. Функцию называют линейной средней квадратической регрессией на .

Теорема. Линейная средняя квадратическая регрессия на имеет вид:

где , , , , .

Метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции, называется методом наименьших квадратов.

27. Показательный закон распределения, графики функции и плотности распределения, числовые характеристики. Показательным распределением непрерывной случайной величины называется такое распределение, которое описывается следующим выражением для плотности вероятности:

,

где – постоянная положительная величина.

Функция распределения вероятности в этом случае имеет вид:

Математическое ожидание случайной величины, имеющей экспоненциальное распределение, получаем на основании общей формулы с учетом того, что при :

.

Интегрируя это выражение по частям, находим: .

Дисперсию для экспоненциального распределения можно получить, используя выражение:

.

Подставляя выражение для плотности вероятности, находим:

Вычисляя интеграл по частям, получаем: .

Числовые характеристики:

1.мат-кое ожидание: M(X)═1/λ

2.дисперсия: D(X)=1/λ², среднее квадратическое отклонение: σ(X)=√D=1/λ

3.вероятность попадания СВ X в заданный интервал:

P(a≤x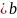 )=e^-λa-e^-λb

Диф-ная Функция: Интегральная функция

28. Нормальный закон распределения, графики функции и плотности распределения. Стандартное нормальное распределение. Функция отраженного нормального распределения. Нормальным называется такое распределение случайной величины , плотность вероятности которого описывается функцией Гаусса:

где – среднее квадратичное отклонение; – математическое ожидание случайной величины.

Г рафик плотности нормального распределения называют нормальной кривой Гаусса.

При а=0, σ =1 распределение называется стандартным нормальным. Плотность вероятности равна:

φ (х)=1/√2π *е^-х/2а функция распределения

F(x)= 1/√2π ∫^x_{-бескон.} *е^{- t/2}dt

Дифференциальная функция

Интегральная ф-ция