
1.
Предмет
и задачи теории вероятностей. Элементы
комбинаторики. Перестановки, размещения,
сочетания. Теорема о числе комбинаций.
Теория
вероятностей
– математическая дисциплина, изучающая
закономерности,возник. в случайных
явлениях. Объектами изучения теории
вероятностей являются случайные
события, величины и функции, которые
характеризуют рассматриваемое случайное
явление. Случайным в теории вероятностей
называют событие, которое при данном
испытании, в данном опыте может либо
произойти, либо не произойти и для
которого имеется определенная вероятность
его наступления.Эл-ты
комбинаторики:сочетание-
наборы,составленные
из n разл-х эл-в по m, кот отлич-ся хотя
бы 1 эл-м
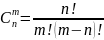 Разменщение-
наборы,сост-е из n
различных эл-в по m
эл-м,кот отлич.либо составом, либо
порядком
Разменщение-
наборы,сост-е из n
различных эл-в по m
эл-м,кот отлич.либо составом, либо
порядком
 Перестановки-
наборы,сост-е из одних и тех же n
разл-х эл-в, и отлич. тольео порядком их
распред-я.
Перестановки-
наборы,сост-е из одних и тех же n
разл-х эл-в, и отлич. тольео порядком их
распред-я. ,
,
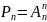 Решение
большинства комбинаторных задач
основано на применении двух основных
правил – правила суммы и правила
произведения.
Решение
большинства комбинаторных задач
основано на применении двух основных
правил – правила суммы и правила
произведения.
Правило суммы: Если элемент А можно выбрать т способами, а элемент В – п способами (причем, ни один из способов выбора элемента А не совпадает со способом выбора элемента В), то выбрать А или В можно т + п способами.Правило произведения: Если элемент А можно выбрать т способами и после каждого такого выбора элемент В можно выбрать п, то выбрать упорядоченную пару (А,В) можно тхп способами.
6.
Зависимые и независимые события. События
независимые в совокупности. Попарно
независимые события.
Если при наступлении события А
вероятность события В
не меняется, то события А
и В
и называются независимыми.Теорема:
Вероятность
совместного появления двух независимых
событий А
и В (произведения А и В ) равна произведению
вероятностей этих событий:
P(A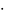 B)=P(A)
P(B).Следствие:
Вероятность
произведения конечного числа независимых
в совокупности событий равна произведению
вероятностей этих событий:.
B)=P(A)
P(B).Следствие:
Вероятность
произведения конечного числа независимых
в совокупности событий равна произведению
вероятностей этих событий:.
Соб.
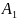 ,…,
,…,
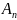 наз-ся независимыми
в совок-ти,
если для любых соб-й
наз-ся независимыми
в совок-ти,
если для любых соб-й
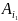 ,
,
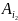 ,…,
,…,
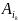 ,
k
,
k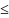 n,
вер-ть
n,
вер-ть
 .Соб.
,…,
наз-ся попарно
независ-ми, если
.Соб.
,…,
наз-ся попарно
независ-ми, если
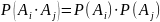 ,
,
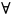 i
i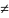 j=
j=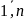 .
.
12. Плотность распределения вероятностей непрерывной случайной величины и ее свойства. Плотность распределения вероятностей случайной величины, являющейся функцией случайной величины.Если существует такая неотрицательная функция f(t), что функция распределения F(x) для каждого
х € (-∞, ∞) представима в виде
F(x) = ∫-∞x f(t)dt, то f(x) называется плотностью распределения случайной величины Х . Плотность распределения непрерывной случайной величины Х можно определить так:
f(x) = F/(x). Свойства плотности распределения:
1) ∫+∞-∞f(x)dx=l;
2) P(a≤X<b)= ∫ ba f(x)dx.
Пример 1. Стрелок трижды стреляет в мишень. Вероятность промаха при одном выстреле равна 0,1. Построить закон и функцию распределения случайной величины Х - числа промахов при 3 выстрелах. Найти математическое ожидание и дисперсию Х
2.
Случайные
события. Операции над событиями, их
свойства.
Случайным в теории вероятностей называют
событие, которое при данном испытании,
в данном опыте может либо произойти,
либо не произойти и для которого имеется
определенная вероятность его
наступления.Вероятность случайного
события
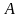 ,
обозначаемая
,
обозначаемая
![]() – числовая мера степени возможности
появления данного события при определенных
условиях. При этом всегда
– числовая мера степени возможности
появления данного события при определенных
условиях. При этом всегда
![]() .Событие
называется достоверным,
если в результате опыта оно обязательно
произойдет. Его вероятность равна
единице. Событие называется невозможным,
если в результате опыта оно не может
произойти; его вероятность равна нулю.
Суммой
нескольких событий называется событие,
заключающееся в появлении хотя бы
одного из них. Несколько событий
.Событие
называется достоверным,
если в результате опыта оно обязательно
произойдет. Его вероятность равна
единице. Событие называется невозможным,
если в результате опыта оно не может
произойти; его вероятность равна нулю.
Суммой
нескольких событий называется событие,
заключающееся в появлении хотя бы
одного из них. Несколько событий![]() называются несовместимыми
в данном опыте, если никакие два из них
не могут появиться одновременно .
называются несовместимыми
в данном опыте, если никакие два из них
не могут появиться одновременно .![]() (
(![]() )
–
Сумма событий.
Это событие, состоящее в том, что
произошло хотя бы одно из двух событий
)
–
Сумма событий.
Это событие, состоящее в том, что
произошло хотя бы одно из двух событий
![]() или
или
![]() или оба
события одновременно. Пересечением
или произведением
событий А и В наз- событие состоящее в
том ,что произошли оба события А и В
одновременно т.е. А,В ,есть множество
содержащее элементарные исходы входящие
в А и в В одновременно .
или оба
события одновременно. Пересечением
или произведением
событий А и В наз- событие состоящее в
том ,что произошли оба события А и В
одновременно т.е. А,В ,есть множество
содержащее элементарные исходы входящие
в А и в В одновременно .
![]() (множество
элементов, принадлежащих А, но не
принадлежащих В)
–
разность
событий
(множество
элементов, принадлежащих А, но не
принадлежащих В)
–
разность
событий
1)![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
![]() 6)
6)
![]() 7)
7)
![]()
8)![]() 9)
9)
![]()
10)
![]() 11)
11)
![]() 12)
12)
![]() 13)
13)![]() 14)
14)
![]() 15)
15)
![]() 16)
16)
![]()
17)![]()
18)![]()
19)
![]() 20)
20)
![]()
21) А(В-С)=(АВ)-(АС)
3.
Классическое определение вероятности.
Свойства вероятностей. Формула сложения
вероятностей. Несовместные события.
Классическое
определение вероятности
связано с определением благоприятствующего
исхода. Исход называется благоприятствующим
данному событию, если его появление
влечет за собой наступление этого
события. Вероятность
события
равна отношению числа равновозможных
благоприятствующих элементарных
исходов к общему числу всех равновозможных
и единственно возможных элементарных
исходов данного испытания:
![]() ,где
,где
![]() –
число благоприятствующих событию
исходов;
–
число благоприятствующих событию
исходов;
![]() – общее число возможных исходов. Из
определения вероятности события
следует, что
– общее число возможных исходов. Из
определения вероятности события
следует, что
![]() ,
поэтому всегда выполняются неравенства
,
поэтому всегда выполняются неравенства
![]() ,
т.е. вероятность
любого события есть неотрицательное
число, не превышающее единицы.
Простейшие свойства вероятностей: 1)
,
т.е. вероятность
любого события есть неотрицательное
число, не превышающее единицы.
Простейшие свойства вероятностей: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
4)
;
3)
;
4)
![]() ;5)
;5)
![]() .Теорема:
Вероятность
появления хотя бы одного из двух
совместных событий равна сумме
вероятностей этих событий без вероятности
их совместного появления:
.Два
события называются несовместными
(несовместимыми), если они не могут
произойти вместе при одном и том же
испытании. Несколько событий называются
несовместными, если они попарно
несовместны.Теорема:
Вероятность
суммы конечного числа несовместных
событий
.Теорема:
Вероятность
появления хотя бы одного из двух
совместных событий равна сумме
вероятностей этих событий без вероятности
их совместного появления:
.Два
события называются несовместными
(несовместимыми), если они не могут
произойти вместе при одном и том же
испытании. Несколько событий называются
несовместными, если они попарно
несовместны.Теорема:
Вероятность
суммы конечного числа несовместных
событий
![]() равна
сумме вероятностей этих событий:
равна
сумме вероятностей этих событий:
![]() .
.
23.
Геометрическое распределение и его
числовые характеристики.
Закон распределения дискретной случайной
величины
![]() называют геометрическим,
поскольку
называют геометрическим,
поскольку
![]() – формула расчета
-го
члена геометрической прогрессии, с
первым членом
– формула расчета
-го
члена геометрической прогрессии, с
первым членом
![]() и знаменателем
и знаменателем
![]() (
(![]() ).
Несложно убедиться в том, что выполняется
условие нормировки:
).
Несложно убедиться в том, что выполняется
условие нормировки:
![]()
Случайная
величина
называется распределенной по закону
геометрической прогрессии с параметром
![]() ,
если
может принимать значения
,
если
может принимать значения
![]() ,
соответствующая вероятность которых
определяется по формуле:
,
соответствующая вероятность которых
определяется по формуле:
![]() ,
где
,
где
![]() .
.
4.
Геометрическое определение вероятности.
Примеры задач на геометрическую
вероятность.
Геометрические
вероятности
– вероятности попадания точки в область
(отрезок, часть плоскости и т.д.). Расс-м
какую-либо обл-ть
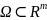 .Предп-м,что
мера
.Предп-м,что
мера
 конечна.пусть случ. эксперимент сос-т
в том,что мы наудачу бросаем в эту об-ть
точку.Термин «наудачу» здесь озн-т,что
вер-ть попадания точки в любую часть
A
конечна.пусть случ. эксперимент сос-т
в том,что мы наудачу бросаем в эту об-ть
точку.Термин «наудачу» здесь озн-т,что
вер-ть попадания точки в любую часть
A не зависит от формы или расположения
A
внутри
,
а зависит лишь от меры области A.
Тогда вероятность того,что точка
попадёт в А:
не зависит от формы или расположения
A
внутри
,
а зависит лишь от меры области A.
Тогда вероятность того,что точка
попадёт в А:
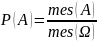 где
где
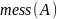 - мера обл. A.
- мера обл. A.
Пример1. Точка бросается наудачу на отрезок [0;1].Вероятность точки попвсть в 0.5 равна 0,т.к.мера мн-ва,сост-го из 1 точки(в данном случае длина есть 0).Вместе с тем попадание в т. 0.5 не явл. невозможным событием,т.к это один из элементарных исходов эксперимента. Пример2.На отрезок АВ длины 1 см. наудачу бросается точка.Н-ти вер-ть того,что эта точка будет ближе к концам отрезка, чем его середине.
![]()
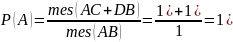
Пример.Парадокс Бертрана.
В круге 1-го радиуса наудачу выбир-ся хорда.Какова вероятность того, что её длина будет больше,чем длина стороны,вписанного в круг правильного треугольника.
Парадокс заключается в некорректной формулировке условия задач с математ. точки зрения. «Выбор наудачу хорды круга» может быть описан с пом. геометрич. опред-я вероятности, т.е. этот «эксперимент» можно по-разному описать с пом. выбора наудачу точки в некот. обл.Здесь слово «эксперимент» взято в кавычки не напрасно:Сказав: «В круге наудачу выбирается хорда» мы ещё не описали физич. эксп-та.Парадокс исчезает сразу, как только получим ответ на вопрос: «Что то значит:в круге выбирается хорда?»
5.
Условные вероятности, их свойства.
Формула сложения условных вероятностей,
формула умножения вероятностей.
Вероятность события
,
вычисленная при условии, что произошло
другое событие
с
вер-тью Р(В)≠0,
называется условной
вероятностью
события
и обозначается
![]() Р(А/В)=Р(АВ)/Р(В)
Вероятность
Р(А/В)=Р(АВ)/Р(В)
Вероятность
![]() появления события
при этих новых условиях называется его
условной вероятностью в отличие от
вероятности
появления события
при этих новых условиях называется его
условной вероятностью в отличие от
вероятности
![]() ,
которая может быть названа безусловной
вероятностью события
.В
тех случаях, когда вероятность события
рассматривается при условии, что имели
место два других события
и
,
которая может быть названа безусловной
вероятностью события
.В
тех случаях, когда вероятность события
рассматривается при условии, что имели
место два других события
и
![]() ,
спользуется условная вероятность
относительно произведения событий В
и С:
,
спользуется условная вероятность
относительно произведения событий В
и С:
![]() .Св-ва
услов. вер-тей: 1.Р(Ω∕В)=1
2.Р(∅/В)=0
3.А⊂С⟹Р(А/В)≤Р(С/В)
4.Р(А ̅/В)=1-Р(А/В)
5.0≤Р(А/В)≤1 6.Формула умножения
вероятностей:Теорема:
Вероятность
произведения двух событий равна
произведению вероятности одного из
них на условную вероятность другого,
вычисленную при условии, что первое
событие имело место: ,
.Св-ва
услов. вер-тей: 1.Р(Ω∕В)=1
2.Р(∅/В)=0
3.А⊂С⟹Р(А/В)≤Р(С/В)
4.Р(А ̅/В)=1-Р(А/В)
5.0≤Р(А/В)≤1 6.Формула умножения
вероятностей:Теорема:
Вероятность
произведения двух событий равна
произведению вероятности одного из
них на условную вероятность другого,
вычисленную при условии, что первое
событие имело место: ,
![]() Р(А)≠0,
Р(В)≠0Общ.
ф-ла умнож-я вер-тей:
Р(А)≠0,
Р(В)≠0Общ.
ф-ла умнож-я вер-тей:
 Формула
сложения услов. вер-тей:
Р(А+С/В)=Р(А/В)+Р(С/В)-Р(АС/В)
Формула
сложения услов. вер-тей:
Р(А+С/В)=Р(А/В)+Р(С/В)-Р(АС/В)
9. Схема Бернулли последовательных испытаний. Формула Бернулли и ее следствие. Наивероятнейшее число наступлений события.
Схема
Бернулли заключ. в след.: проводится n
последовательных испытаний, которые:
независимы; в любом испытании возможны
только 2 исхода (A
и
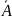 );
вероятности этих исходов постоянны и
не изменяются от испытания к испытанию.
);
вероятности этих исходов постоянны и
не изменяются от испытания к испытанию.
Под независимыми понимаются такие эксперименты, в которых любые события, возникающие в разных экспериментах, являются независимыми в совокупности.
p = P(A) q = P( ) = 1 – p
Наступление события A обычно называют успехом, а ненаступление – неудачей.
Формула Бернулли.
Вероятность того, что в схеме Бернулли из n испытаний успех наступит ровно m раз равна
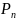 (m)
=
(m)
=
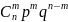
Следствие:
Пусть m1
и
m2
 Z,
Z,
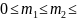 n.
Тогда вероятность того, что в схеме
Бернулли успех наступит не менее m1
и не более m2
раз в n
испытаниях равна
n.
Тогда вероятность того, что в схеме
Бернулли успех наступит не менее m1
и не более m2
раз в n
испытаниях равна
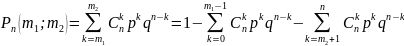
Определение: Число наступлений события A (успеха) называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события A любое другое количество раз.
Теорема.
Наивероятнейшее
число наступлений события
в
независимых
испытаниях схемы Бернулли заключено
между числами
![]() и
и
![]() .
При
этом, если
.
При
этом, если
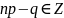 ,
то наивероятнейших чисел два, а именно
,
то наивероятнейших чисел два, а именно
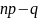 и
и
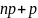 .
.
16. Математическое ожидание, дисперсия, среднее квадратическое отклонение и моменты непрерывной случайной величины. Мода и медиана непрерывной случайной величины. Неравенство Коши-Буняковского. Дисперсией непрерывной СВ наз-ся значение интеграла:
![]() .
.
Среднее квадратичное отклонение непрерывной СВ - корень квадратный из дисперсии:
![]() .
.
Мода
(![]() )
непрерывной СВ
– значение, кот соответствует максимальное
знач ее плотности вероятности.
)
непрерывной СВ
– значение, кот соответствует максимальное
знач ее плотности вероятности.
Медианой
(![]() )
непрерывной СВ
- значение, кот опр равенством:
)
непрерывной СВ
- значение, кот опр равенством:
![]() .
.
Нерав-во Коши-Буняковского: для любых СВX и Y
M(|X Y|)≤(M(X2))1/2 (M(Y2))1/2
8.Формула полной вероятности и формула Байеса.
Формула полной вероятности:
Пусть H1…Hn – полная группа событий и P(Hi)>0, i=1,n⁻⁻, тогда для любого события А
Р(А)=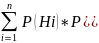 )
)
Формула Байеса:
Пусть дана полная группа событий H1,…,Нn и некоторое событие А, тогда для любых К от 1 до n условная вероятность события Нк при условии, что произошло событие А вычислится по формуле
Р(Нк/A)=
11.
Понятие случайной величины(СВ) и ее
закона распределения. Функция
распределения случайной величины и ее
свойства. График функции распределения
случайной величины..
Случайной
величиной
наз-ся переменная величина, к-рая в
зависимости от исхода испытания случайно
принимает одно значение из множества
возможных значений.Случайная величина
обычно обозначается прописной латинской
буквой (![]() ),
ее конкретные значения – строчными
буквами (
),
ее конкретные значения – строчными
буквами (![]() ).СВ
делятся на дискретные и непрерывные,
выделяют также смешанные 1) Величина
наз-ся дискретной,
если она м. принимать определенные,
фиксированные значения. 2) СВ вназывается
непрерывной,
если она может принимать значения,
сколь угодно мало отличающиеся друг
от друга.Законом
распределения
СВ называется
совокупность пар чисел (
).СВ
делятся на дискретные и непрерывные,
выделяют также смешанные 1) Величина
наз-ся дискретной,
если она м. принимать определенные,
фиксированные значения. 2) СВ вназывается
непрерывной,
если она может принимать значения,
сколь угодно мало отличающиеся друг
от друга.Законом
распределения
СВ называется
совокупность пар чисел (![]() ),
где
),
где
![]() – возможные значения случайной величины,
а
– возможные значения случайной величины,
а
![]() – вероятности, с которыми она принимает
эти значения, причем
– вероятности, с которыми она принимает
эти значения, причем
![]() .закон.
Как для
дискретной величины, так и для непрерывной
вводится понятие функции
распределения.
Функция
.закон.
Как для
дискретной величины, так и для непрерывной
вводится понятие функции
распределения.
Функция
F(x) = Р(Х < х), х € (-∞, ∞) называется функцией распределения случайной величины Х Для дискретной случайной величины Х функция распределения имеет вид F(x)=∑pi
i:x,<x
Свойства функции распределения:
1) если х1 < х2 , то F(х1)≤F(x2), то есть F(x) - неубывающая функция;
2) F(-∞)=О, F(∞) =1; 3) функция F(x) непрерывна слева, то есть lim F(x) = F(y). x→y-0
Кроме того, для любых а < Ь верно равенство Р(а ≤Х < Ь) = F(b) - F(a).
y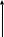
1

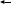


1 2 x
18. Ковариацией случайных величин X и У называют математическое ожидание произведения отклонений этих величин: рху = М{\Х-М<Х)][У-М(У)]}.
Для вычисления ковариации дискретных вел-н испол-т формулу mxy=E*E [х1-М(Х)][у/-М(У)]р(х,Уi),
а для непрерывных величин—формулу mxy=SS[х—М(ХШу-М(У)]f(х, у)dxdy.
Ковариация равна нулю, если X и У независимы; следовательно, если ковариация не равна нулю, то X и У — зависимые случайные величины. Ковариация служит для характеристики связи между величинами X и У.
Две случайные величины X и У называют корелированными, если их ковариация отлична от нуля; Х и У называют некоррелированными величинами, если ковариация равна нулю.
Дисперсию СВ У - функции случайной величины Х(У=(р(Х)), имеющей дифференциальную функцию f(х), можно определить по формулам:
М(У) = М(ф(х)) = Sф(х)f(х)dх
D(У) = В(ф(х)) = Sф2{х)/(х)dх-М2{У).
10. Предельные теоремы для схемы Бернулли (Теорема Пуассона, локальная и интегральная теоремы Муавра-Лапласа). Функции Гаусса и Лапласа.
В случае, когда число испытаний велико, формулу Бернулли применять неудобно. Для больших существуют приближенные формулы. Точность этих формул увеличивается с возрастанием .
Теорема
Пуассона:Предположим,
что произведение np
=
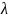 является постоянной величиной, когда
n
неограниченно возрастает, тогда для
любого фиксированного m
и
является постоянной величиной, когда
n
неограниченно возрастает, тогда для
любого фиксированного m
и
 постоянного
постоянного
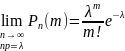 На
практике эта теорема применяется
следующим образом. Если n
велико, а p
мало,
На
практике эта теорема применяется
следующим образом. Если n
велико, а p
мало,
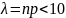 ,
то
,
то
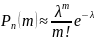
Теорема
Пуассона с оценкой погрешности: Пусть
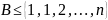 произвольное множество целых
неотрицательных чисел от 0 до n,
произвольное множество целых
неотрицательных чисел от 0 до n,
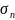 – число успехов n
испытаний схемы Бернулли,
тогда
– число успехов n
испытаний схемы Бернулли,
тогда

Замечание: Если мало значение q1 то по Пуассоновским приближениям можно воспользоваться для числа неудач.
Если
же n
достаточно велико, а p
не слишком близко к нулю или единице,
то имеет место теорема: Локальная
теорема Муавра-Лапласа: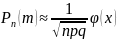 ,
где
,
где
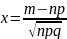 ,
,
а
 Функция
Функция
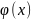 называется ф-ей Гауса. Эта функция
затабулирована
называется ф-ей Гауса. Эта функция
затабулирована
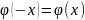 – ф-ия Гауса чётная. При
достаточно больших n
вероятность того, что событие A
в схеме Бернулли наступило не менее m1
и не более m2
раз в n
испытаниях, при условии, что p
не слишком близко к 0 или 1, вычисляется
с помощью след. теоремы:
Интегральная теорема Муавра-Лапласа:
– ф-ия Гауса чётная. При
достаточно больших n
вероятность того, что событие A
в схеме Бернулли наступило не менее m1
и не более m2
раз в n
испытаниях, при условии, что p
не слишком близко к 0 или 1, вычисляется
с помощью след. теоремы:
Интегральная теорема Муавра-Лапласа:
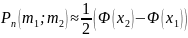 где
где
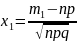 ,
,
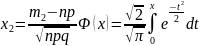 Ф-ия
Ф-ия
 (x)
называется ф-ией Лапласа, она также
затабулирована, она нечётная, т.е. Ф(-x)
= Ф(x)
(x)
называется ф-ией Лапласа, она также
затабулирована, она нечётная, т.е. Ф(-x)
= Ф(x)
