I. Числовые ряды

§ 1. Основные понятия

Пусть дана некоторая бесконечная последовательность чисел

. (1)

Выражение вида

(2)

называется бесконечным числовым рядом, или просто рядом. Числа (1) называются членами ряда. Число а_п, где п - не фиксировано - общим членом ряда.

Складывая последовательно члены ряда, получаем последовательность

(3)

которая называется последовательностью частичных сумм или последовательностью отрезков ряда.

Определение. Если существует конечный предел S последовательности частичных сумм (3), то его называют суммой ряда (2) и пишут

.

Ряд (2) в этом случае называют сходящимся .

Если последовательность частичных сумм (3) расходится, то и ряд (2) называется расходящимся и ему в этом случае не приписывают никакую сумму.

Например, суммируя бесконечную геометрическую прогрессию, получаем ряд

. (4)

При q  1 его частичная сумма примет вид:

.

При |q| < 1, получаем:

, (5)

следовательно, ряд (4) сходится. При |q|  1, ряд (4) расходится.

Ряд 1+1+1+...+1+... расходится, так как .

Теорема 1. Если ряд (2) сходится, то его общий член стремится к нулю при п  .

Действительно, если ряд (2) сходится, то

,

следовательно,

.

Но легко убедиться в том, что стремление к нулю общего члена не обеспечивает сходимости ряда. Другими словами, этот важный необходимый признак сходимости ряда не является достаточным.

Гармонический ряд

расходится, но его общий член стремится к нулю, т. е.

.

Если в ряде (2) отбросить первые т членов, то получается ряд:

, (6)

называемый остатком ряда (2).

Теорема 2. Если сходится ряд (2), то сходится и любой его остаток (6). Обратно, из сходимости остатка (6) вытекает сходимость исходного ряда (2).

Если остаток ряда сходится, то его сумму будем обозначать r_m.

Теорема 3. Если ряд (2) сходится, то сумма r_m его остатка стремится к нулю при т .

Справедливы следующие основные свойства сходящихся рядов:

1^о. Если члены сходящегося ряда (2) умножить на одно и то же число b, то его сходимость не нарушается, а сумма умножается на b.

2^о. Два сходящихся ряда

можно почленно складывать или вычитать и при этом получаем сходящийся ряд, причем

Пример 1. Показать, что ряд сходится.

Решение. Составим частичную сумму S_n первых п членов ряда:

. (7)

Разложим общий член ряда на простейшие дроби, пользуясь известным методом неопределенных коэффициентов:

.

Отсюда получаем:

.

Поэтому

.

Перепишем сумму (7) так:

Переходя к пределу, получаем:

.

Таким образом, данный ряд сходится и его сумма равна

.

Пример 2. Рассмотрим ряд . Покажем, что он сходится.

Решение. Распишем ряд в развернутом виде:

или

Члены ряда образуют бесконечно убывающую геометрическую прогрессию со знаменателем . Следовательно, данный ряд сходится и сумму его вычисляем по формуле (5)

.

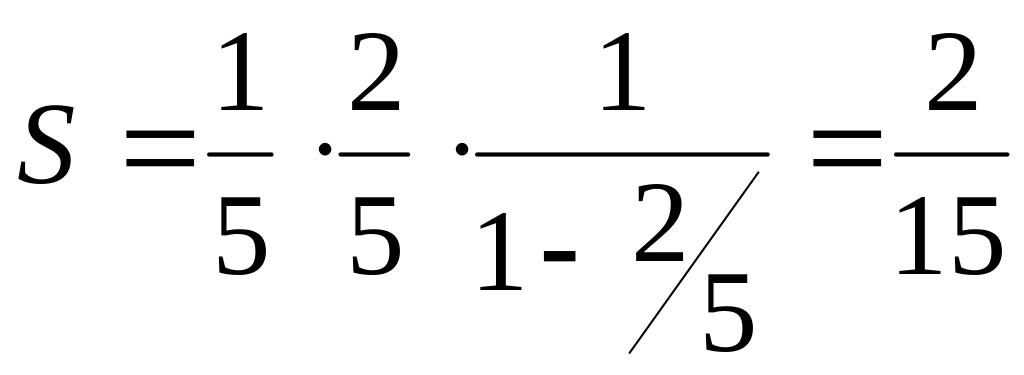Пример 3. Покажем, что ряд расходится.

Решение. Проверим выполнение необходимого условия сходимости для данного ряда.

.

Так как общий член ряда не стремится к нулю при п  , то заданный ряд не удовлетворяет необходимому признаку сходимости и, следовательно, расходится.