3.5. Метод термодинамических потенциалов

3.5.1. Определение и физический смысл потенциалов. Предположим, что находящаяся во внешней среде система предоставлена самой себе и над ней не производится никакой работы. В ней будут происходить самопроизвольные процессы, приводящие её в равновесное состояние. В формуле (3.23) следует теперь положить 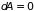, что приводит к неравенству

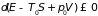. (3.28)

Иными словами, при всех процессах в системе, взаимодействующей со средой, величина 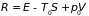не увеличивается, а в равновесии достигает минимума. Для замкнутой системы ( и 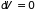) из (3.28) следует закон возрастания энтропии .

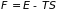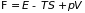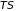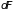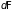Максимальная работа, производимая телом при изотермо-изохорическом и изотермо-изобарическом процессах была определена через убыль функций и , которые получили название свободная энергия и основной термодинамический потенциал (потенциал Гиббса), соответственно. Функция называется связанной энергией. Их изменение ( и ) также, как и внутренней энергии ( ) в теплоизолированной системе, является мерой работы в незамкнутых системах при изотермо-изохорических и изотермо-изобарических процессах. Для незамкнутых систем неравенство (3.28) при и 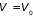(или ) принимает вид

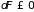и 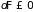. (3.29)

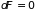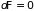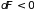Таким образом, изменение как свободной энергии, так и потенциала Гиббса, подобно энтропии, является критерием обратимости ( и ) или необратимости ( и 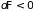) процессов и определяет их направление в незамкнутых системах.

Примером необратимого изотермо-изохорического процесса может служить растворение какого-либо вещества (соли, сахара) в значительном объеме растворителя (воды) при постоянных температуре и объеме раствора. Поэтому, согласно (3.29), свободная энергия раствора будет меньше, чем сумма свободных энергий растворителя и вещества.

Метод термодинамических потенциалов (характеристических функций) был развит Гиббсом. Это аналитический метод, базирующийся на основном термодинамическом равенстве, в котором учитывается работа всех внешних сил

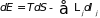(3.30)

Идея метода состоит в том, что данное равенство позволяет для системы в различных условиях ввести некоторые термодинамические потенциалы, изменение которых в квазистатическом процессе является полным дифференциалом. Используя этот факт, составляются уравнения, необходимые для анализа того или иного явления.

Простые системы с постоянным числом частиц описываются уравнением (3.8):

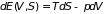, (3.31)

где объем и энтропия являются независимыми переменными. Остальные параметры системы определяются, если известна функция :

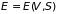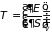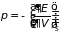; . (3.32)

Внутренняя энергия 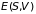в качестве термодинамического потенциала с практической точки зрения неудобна тем, что одна из независимых переменных – энтропия не может быть измерена непосредственно. Если независимыми являются не и , а какие-либо другие величины, то энергия не является характеристической функцией (потенциалом) этих величин. При других переменных вводятся иные потенциалы. Так, вычитая из обеих частей уравнения (3.31) дифференциал 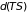, получим

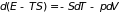. (3.33)

Такая операция дифференциальной формы называется преобразованием Лежандра. Учитывая, что 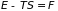есть свободная энергия, определяем ее как потенциал относительно переменных объема и температуры

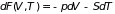. (3.34)

Прибавляя к обеим частям этого уравнения дифференциал 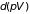находим потенциал Гиббса по отношению к переменным давления и температуры

. (3.35)

Когда на систему действуют, кроме механических сил , и другие немеханические силы (электрические, магнитные и т.д.), то в (3.35) нужно добавить их работу :

.

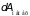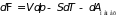Отсюда следует, что убыль потенциала Гиббса при изотермо-изобарных процессах равна работе системы против действующих на нее немеханических сил. Применение преобразования Лежандра с дифференциалом к (3.31) приводит к еще одному потенциалу – энтальпии 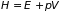относительно энтропии и давления :

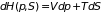. (3.36)

Физический смысл энтальпии в том, что при изобарных процессах её изменение равно поглощенному количеству теплоты. По этой причине потенциал 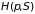называют еще тепловой функцией или теплосодержанием системы.

Следствием формул (3.34)-(3.36) являются равенства

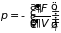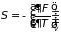; ; (3.37.а)

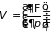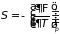; ; (3.37.б)

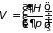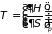; , (3.37.в)

которые совместно с (3.32) определяют основные термодинамические параметры системы при различных процессах. Первое в (3.37.а) играет особую роль в термодинамике и получило название уравнение состояния.

Все термодинамические потенциалы являются, во-первых, аддитивными и однозначными функциями состояния, во-вторых, их убыль при соответствующих условиях определяет работу против действующих на нее сил. Кроме того, с помощью основного термодинамического неравенства они позволяют для необратимых процессов установить общие критерии термодинамического равновесия и устойчивости систем.

Для сложных систем, состояние которых, кроме объема (давления), зависит от других внешних параметров 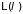полученные выражения для дифференциалов потенциалов усложняются за счет добавления в их правые части соответствующих слагаемых 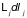(3.30).

3.5.2. Дифференциальные соотношения термодинамики. Уравнения Гиббса-Гельмгольца. Поскольку (3.31), (3.34)-(3.36) представляют полный дифференциал соответствующих потенциалов, то приравнивая смешанные производные , , 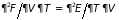…, получаем уравнения

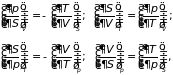(3.38)

которые носят название дифференциальные соотношения термодинамики (или перекрестные соотношения Максвелла). Справедливы и обращенные равенства, например:

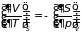, и т.д.

Уравнения (3.38) связывают два свойства системы. В частности, первое из них определяет изменение температуры системы при ее адиабатическом расширении через изменение давления при изохорном подводе тепла. Установление подобных связей и составляет содержание метода термодинамических потенциалов.

Дифференциальные соотношения термодинамики позволяют не только сопоставлять макроскопические характеристики материальных систем, но и заменять исследование одного свойства изучением другого, связанного с ним. Это особенно важно, когда нужно уйти от неизмеряемых (или трудно измеряемых) величин, например, энтропии.

Метод дифференциальных соотношений термодинамики представляет собой общее и эффективное средство исследования конкретных свойств самых разнообразных систем. Общность обусловлена тем, что дифференциальные соотношения являются следствием основного уравнения термодинамики, выражающего такой универсальный принцип, как закон сохранения энергии. Чрезвычайно важным является и то, что дифференциальные соотношения термодинамики отражают глубокую внутреннюю связь между разнородными явлениями, отражают единство различных форм движения материи.

Кроме установленных соотношений между различными свойствами системы (3.38), существует и связь между термодинамическими потенциалами. Так, из определения свободной энергии ( ), энтальпии (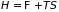 ) и формул (3.37.а), (3.37.б) для нетрудно получить уравнения

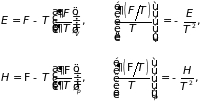(3.39)

именуемые уравнениями Гиббса-Гельмгольца. Они показывают, что при известных температурных зависимостях внутренней энергии (или энтальпии) системы могут быть найдены её свободная энергия (или потенциал Гиббса):

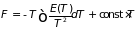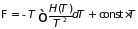, (3.40)

3.5.3. Потенциалы систем с переменным числом частиц. Энергия, энтропия и объем суть аддитивные функции. Поэтому основное термодинамическое равенство (3.31) может быть записано также для их удельных значений, отнесенных к единице массы или одной частицы:

,

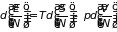где – число частиц в системе. Это равенство не зависит от того, по какой причине изменяются удельные значения. Считая переменными, кроме , , и число частиц, имеем

, (3.41)

где обозначено

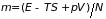. (3.42)

Из (3.41) следует

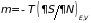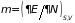; (3.43)

Последние равенства доказывает тождественность величины химическому (парциальному) потенциалу, входящему в большое каноническое распределение Гиббса. Формула (3.41) играет роль основного термодинамического равенства для систем с переменным числом частиц.

Если система неоднородная, то наряду с изменением общего числа частиц могут проходить процессы взаимопревращения частиц разного сорта. В этом случае в равенстве (3.41) вместо последнего слагаемого необходимо ввести сумму по всем сортам частиц – , где 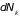– изменение числа частиц -го сорта, а 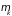– соответствующий им химический потенциал. Такие же слагаемые входят в дифференциалы потенциалов , 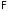и , в частности,

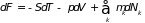(3.44)

Химический потенциал из этих выражений, очевидно, равен

. (3.45)

Таким образом, можно получить дифференцированием любого из термодинамических потенциалов по числу частиц. Однако в каждом случае он будет выражен через различные независимые переменные. Простой формулой определяется связь химического потенциала с потенциалом Гиббса (3.42)

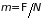. (3.46)

При анализе систем с переменным числом частиц чаще всего используют такой термодинамический потенциал, дифференцирование которого по соответствующим переменным позволяет найти числа частиц в системе 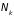каждого сорта. Чтобы его найти проведем преобразование Лежандра формулы (3.44)

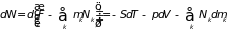. (3.47)

Здесь функция

, (3.48)

Называется большим термодинамическим потенциалом. Его знание позволяет из (3.47) определить

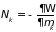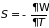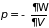; ; . (3.49)