Форма распределения

В симметричных рядах распределения значения моды и медианы совпадают со средней величиной (=Мо=Ме), в умеренно асимметричных они соотносятся таким образом: 3(-Ме)= -Мо

Для примера 1 =36,14; Мо=Ме=36 – симметричный ряд

Для примера 2 =16,3; Мо=15,3; Ме=16 – умеренно асимметричный ряд

(3(-Ме)=0,9; -Мо=1)

Квартили (Q) – значения вариантов, которые делят упорядоченный ряд по объему на 4 равные части. Выделяют три квартиля. Второй квартиль – это медиана (Ме=Q₂).

Первый квартиль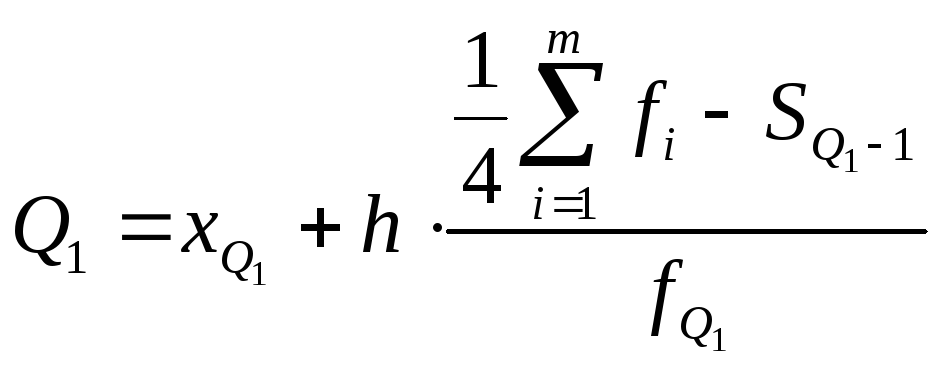

Третий квартиль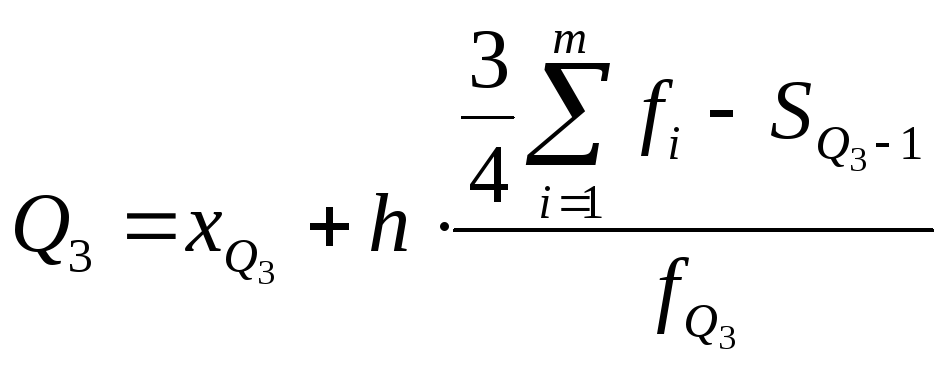

- общая формула k-ого квартиля

Пример 2

Влажность, % (xi)	Число образцов (fi)	Накопленная частота (Si)
До 14 14 – 16 16 – 18 18 – 20 20 и более	20 30 25 15 10	20 50 75 90 -
Итого:	100

N₁=25,75; N₂=50,5; N₃=75,25

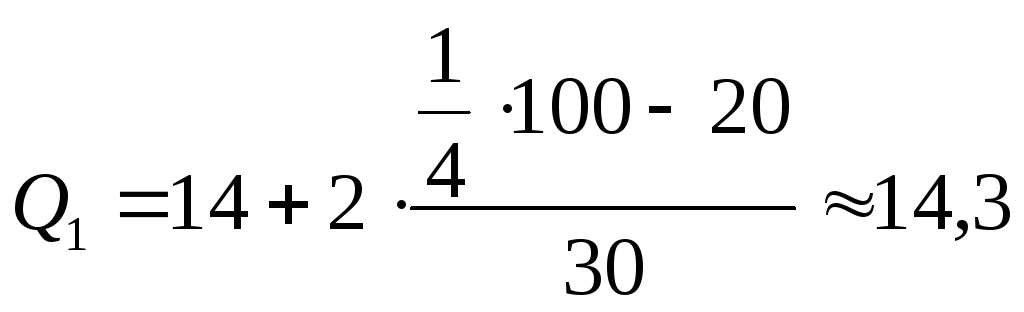
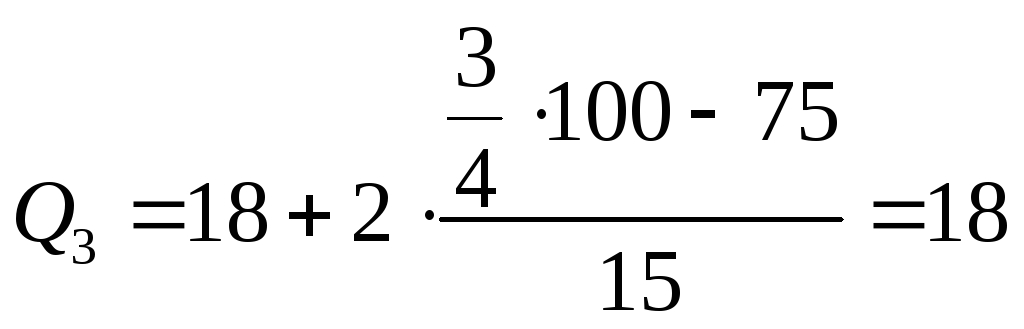
Вывод: для ранжированных данных 25% товаров содержат процент влажности, не превышающий 14,3%, у 75% товаров процент влажности не превышает 18%

Обобщение: Квантилем уровня q (или q-квантилем) называется такое значение x_q случайной величины, при котором интегральная функция ее распределения принимает значение, равное q, т. е. F(x_q)=P(X<x_q)=q.

Очевидно, что введенная выше медиана случайной величины есть квантиль уровня 0,5 (2-ой квартиль), т. е. Me(X)=x_0,5. Квантили x_0,25 и x_0,75 (1-ый и 3-ий квартили) получили название соответственно верхнего и нижнего квантилей.

Начальным моментом k-ого порядка случайной величины X называется математическое ожидание k-ой степени этой величины m_k=M(X^k).

Центральным моментом k-ого порядка случайной величины X называется математическое ожидание k-ой степени отклонения случайной величины X от ее математического ожидания. _k=M[X-M(X)]^k.

Момент	Случайная величина
	дискретная	непрерывная
начальный
центральный

В таблице: x_i - значения, которые принимает дискретная случайная величина с вероятностями p_i, f(x) - плотность вероятности непрерывной случайной величины, а - математическое ожидание.

Нетрудно заметить, что при k=1 первый начальный момент случайной величины X есть ее математическое ожидание m₁=M(X)=a, при k=2 второй центральный момент - дисперсия _k=D(X).

Центральные моменты могут быть выражены через начальные моменты по формулам:

₁ = 0

₂ = m₂ - (m₁)²

₃ = m₃ - 3m₁m₂ + 2(m₁)³

₄ = m₄ - 4m₁m₃ + 6(m₁)²m₂ - 3(m₁)⁴

Первый начальный момент (математическое ожидание) характеризует среднее значение или положение распределения случайной величины на числовой оси.

Второй центральный момент (дисперсия) характеризует степень рассеяния распределения случайной величины относительно математического ожидания.

Третий центральный момент служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на куб среднего квадратического отклонения случайной величины. Полученная величина называется коэффициентом асимметрии случайной величины . Если распределение симметрично относительно математического ожидания, то А=0. Кривая более пологая справа имеет положительную асимметрию (А>0), более пологая слева - отрицательную (А<0).

Четвертый центральный момент служит для характеристики крутости (островершинности или плосковершинности) распределения.

Эксцессом (коэффициентом эксцесса) случайной величины называется число (число 3 вычитается, т. к. для нормального распределения ). Кривые более островершинные, чем нормальная, обладают положительным эксцессом, более плосковершинные - отрицательным эксцессом.