4 Определение обратной матрицы. Доказать что у каждой обратимой матрицы существует лишь одно обращение.

Определение: Квадратная матрица А называется обратимой если существует такая квадратная матрица Х что АХ=ХА=Е. (1)

Каждая матрица Х удовлетворяющая равенству (1) называется обратной матрице А или обращением матрицы А. Обратная матрица к матрице А обозначается А^-1

А А^-1= А^-1А=Е Отсюда следует что для матрицы А^-1 обратной будет (А^-1)^-1=А

Теорема: У каждой обратимой матрицы существует единственное обращение.

Доказательство: Предположим что у матрицы А существует наряду с Х еще одна обратная матрица У, т.е. АУ=Е. Тогда

(ХА)У=ЕУ=У ┐

Х(АУ)=ХЕ=Х ┘Следовательно Х=У. Т.е. у матрицы А существует единственное обращение.(ч.т.д.)

5. Определение обратной матрицы. Доказать что (АВС)^-1=С^-1В^-1А^-1.

Определение: Квадратная матрица А называется обратимой если существует такая квадратная матрица Х что АХ=ХА=Е. (1)

Каждая матрица Х удовлетворяющая равенству (1) называется обратной матрице А или обращением матрицы А. Обратная матрица к матрице А обозначается А^-1

А А^-1= А^-1А=Е Отсюда следует что для матрицы А^-1 обратной будет (А^-1)^-1=А (3)

Теорема: Если квадратные матрицы А, В, С одного и того же порядка обратимы, то их произведение тоже обратимо и (АВС)^-1=С^-1В^-1А^-1.

Доказательство: А(В(СС^-1)В^-1)А^-1=Е и С^-1(В^-1(А^-1А)В)С=Е (ч.т.д.)

Для любого натурального m по определению А^m=А*А*…*А – m-раз.

По определению А⁰=Е.

Определение: Для каждой обратимой матрицы А, А^-2=А^-1*А^-1; А^-3= А^-1*А^-1*А^-1 (4)

Из (3) и (4) следует что для каждой обратимой матрицы А и любых целых чисел р и q имеют место обычные правила действия со степенями:

А^рА^q =А^{р+ q}

(АВ)^р=А^рВ^р если АВ=ВА

(А^р)^q=А^р*q

6. Доказать что в результате транспонирования обратимой матрицы получается снова обратимая матрица и (A’)^-1=(A^-1)’.

Операция транспонирования матрицы и её свойства.

Определение: Матрица А’ получающаяся из матрицы А путем замены строк столбцами называется транспонированной по отношению к матрице А.

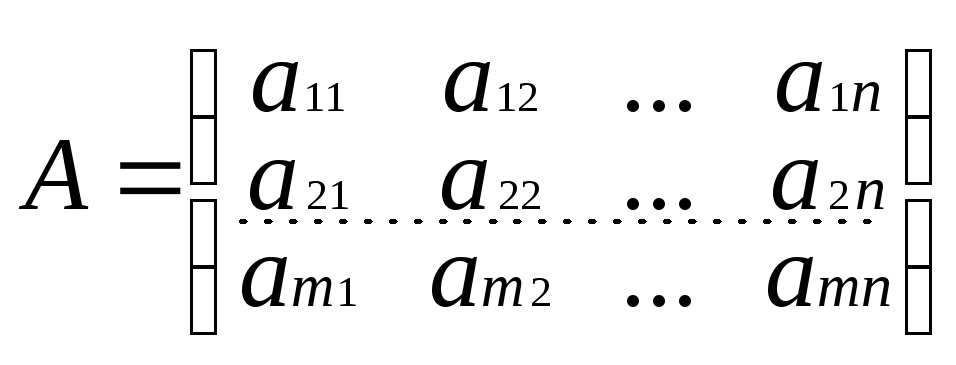
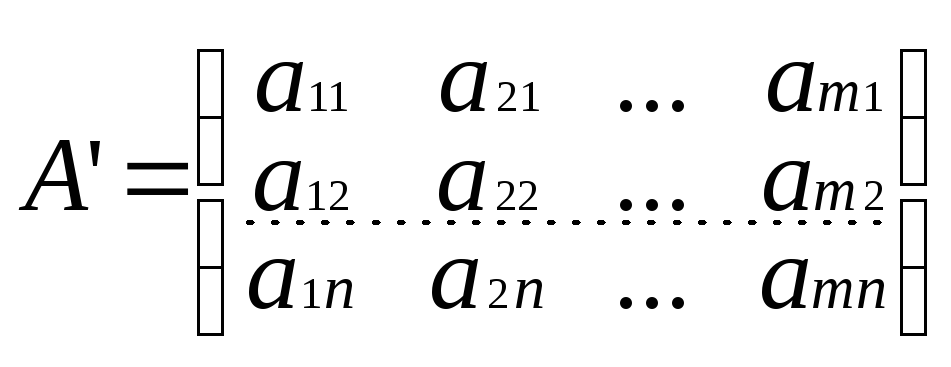
Справедливы следующие правила транспонирования матриц:

1. (αА+αВ)’=αA’ + αB’

2. (AB)’=B’A’

Идея доказательства показать что матрицы (AB)’ и B’A’ имеют одинаковую размерность и у них равны соответствующие элементы.

Определение: Если А – произвольная квадратная матрица и A=A’ (-A=A’), то матрица А называется симметрической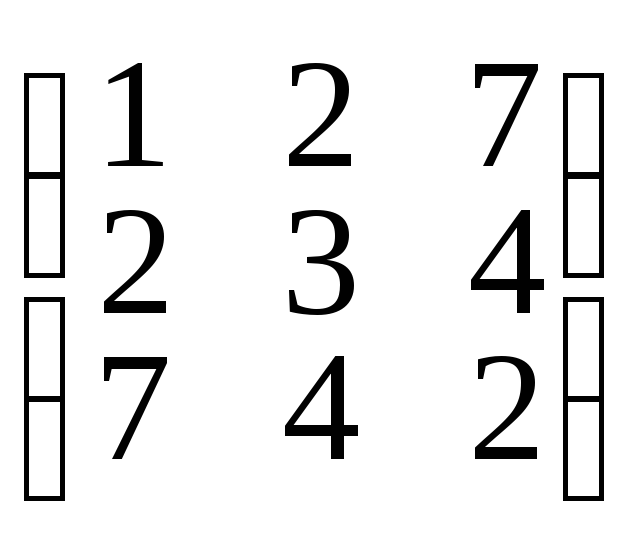 или кососимметрической

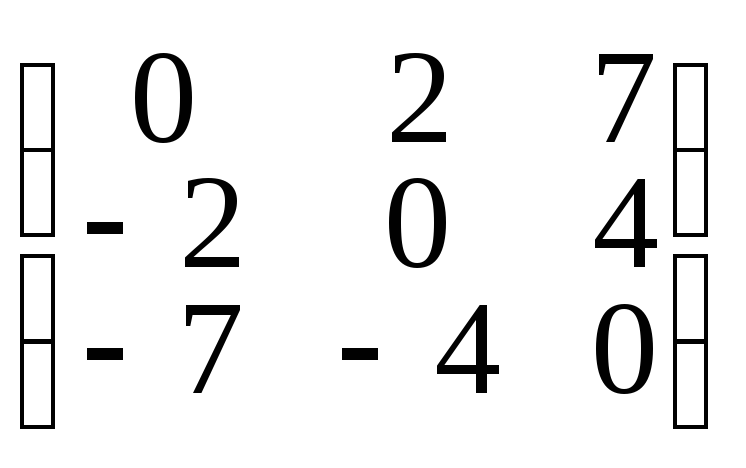
Теорема: В результате транспонирования обратимой матрицы А получается снова обратимая матрица и (A’)^-1=(A^-1)’.

Доказательство: Применим правила транспонирования к соотношению АХ=ХА=Е:

(АХ)’=(ХА)’=Е’

А’Х’=Х’А’=Е

Из определения обратной матрицы следует что (A’)^-1= Х’=(A^-1)’(ч.т.д.)

7. Блочные матрицы. Сложение и умножение блочных матриц. Теорема об определителе квазитреугольной матрицы.

Прямоугольную матрицу А можно вертикальными и горизонтальными линиями разбить на прямоугольные клетки(блоки). В частности матрица может быть разбита только горизонтальными или только вертикальными линиями. (А_α,β)_s,t – блочная матрица. Рассмотрим две матрицы А и В одинаковой размерности и с одинаковым разбиением на блоки. Соответствующие блоки А_α,β и В_α,β имеют одинаковую размерность m_α x n _β , α=1..s, β=1..t. Тогда в соответствии с правилом сложения матриц операция сложения блочных матриц одинаковых размеров с одинаковым разбиением на блоки, производится точно также как если бы вместо блоков стояли числовые элементы.

Чтобы распространить правило умножения матриц на блочные матрицы необходимо чтобы все горизонтальные размеры блоков первой матрицы совпали с соответствующими размерами второго сомножителя. Число столбцов блока А_α,β равно числу строк блока В_β,с .

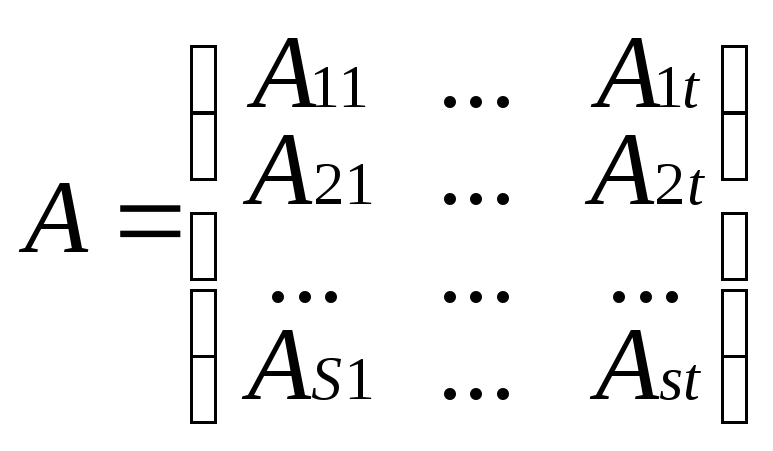
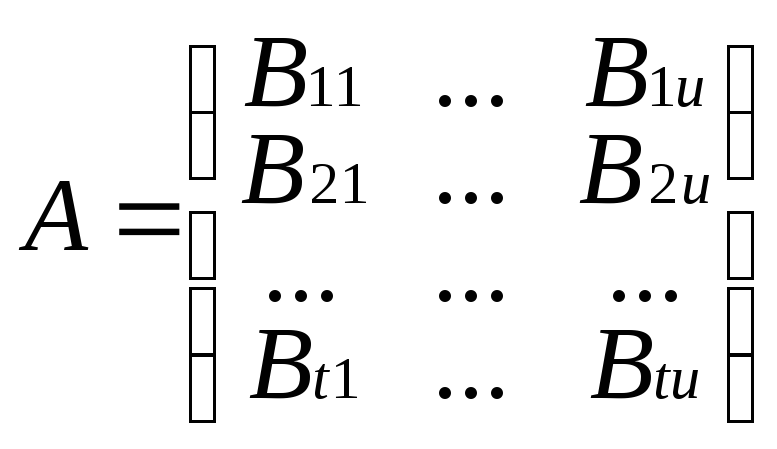
Β изменяется от 1 доt, с изменяется от 1 до u. Таким образом возможно умножение матриц А и В формально также как если бы вместо блоков стояли числовые элементы.

Определение: Квадратная матрица у которой все элементы расположенные под(над) главной диагональю равны 0 называется верхней(нижней) треугольной матрицей. Аналогичные понятия вводятся и для блочных матриц.

Определение: Блочная матрица А называется верхней(нижней) квазитреугольной матрицей если все диагональные блоки и сама матрица А квадратные матрицы, и все не диагональные блоки расположенные под(над) диагональными блоками нулевые матрицы.

Определение: Блочная матрица А называется квазидиагональной если все диагональные блоки и сама матрица А квадратные матрицы, а все недиагональные блоки – нулевые матрицы.

Теорема: Определитель квазитреугольной матрицы связан с определителем диагональных матриц следующим соотношением:

(♀) где П – произведение.

Доказательство: Рассмотрим сначала квазитреугольную матрицу где А₁₂=0, , ,

По определению

Т.к. А₁₂=0 то из всех произведений могут быть ≠0 только те в которых индексы . Вследствие этого остальные индексы могут принимать значения только из множества . В этих условиях число инверсий в перестановке равно:

т.е.

Учитывая это находим что

Отсюда следует что

Рассматривая в общем случае квазитреугольную матрицу

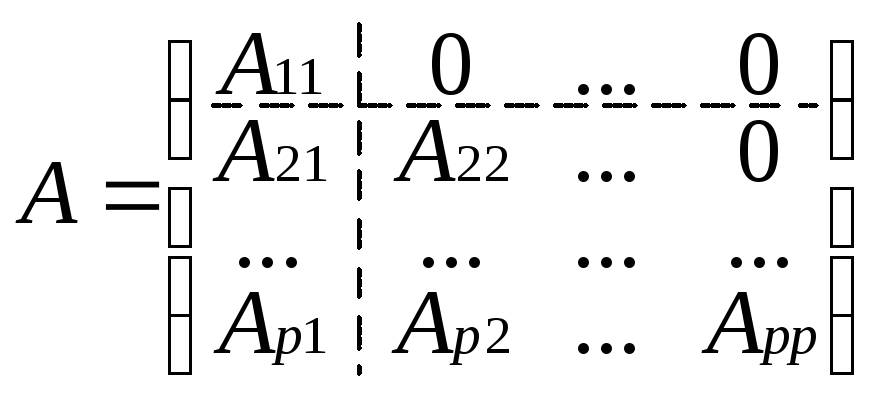
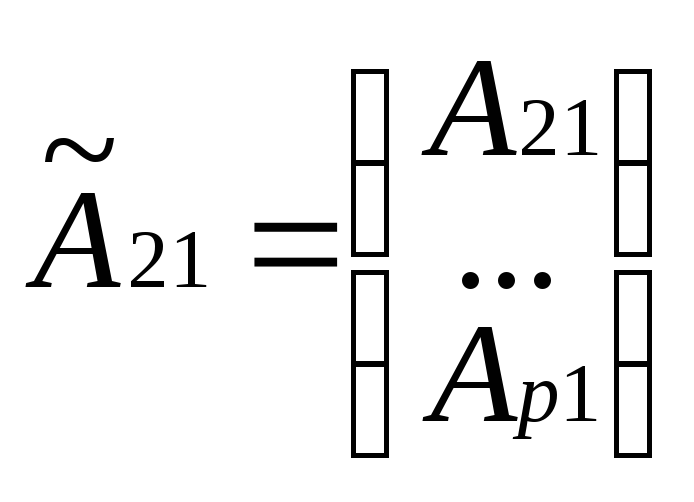
Как матрицу где согласно (*) будем иметь . Матрица снова квазитреугольная. Проделав над ней туже операцию, получим . После (р-1) таких шагов придем к (♀).

Аналогично доказывается равенство (♀) применительно к верхней квазитреугольной матрице.(ч.т.д.)