3.1.1. Оценка погрешности приближений процесса итераций

Пусть и - два последовательных приближения системы (3.2). Тогда для приближения справедлива оценка

:,

если выполнено первое условие теоремы 3.1, или

,

если выполнено второе условие теоремы 3.1. Процесс итерации заканчивают, когда указанные оценки свидетельствуют о достижении заданной точности ε.

или

3.1.2. Приведение линейной системы к виду, удобному для итерации:

Сходимость накладывает жесткие условия на коэффициенты данной линейной системы . Однако, если , то с помощью линейного комбинирования уравнений системы, последнюю всегда можно заменить эквивалентной системой , такой, что условия сходимости будут выполнены. Умножим уравнение (3.1) на матрицу, где - матрица с малыми по модулю, одинаковыми элементами. Тогда будем иметь:

или , где и .

Все элементы матрицы ε выбираем одинаковыми из условия . Это обеспечивает выполнение достаточного условия сходимости метода.

Пример 3.1 Решить систему методом итераций в Mathcad с тремя верными цифрами после запятой

Точность вычислений

Решение исходной системы матричным методом

Линейными преобразованиями добиваемся диагонального преобладания.

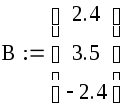
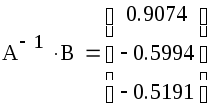
2*I+II

II+2*III

II-3III

Преобразуем к виду, удобному для итераций.

q-это норма матрицы «с»

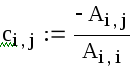
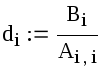
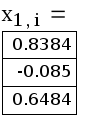
В качестве начального приближения возьмем столбец свободных членов, сделаем 6 приближений, вектор разностей между соседними приближениями обозначим z. Результаты поместим в матрицу x.

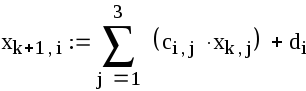
Ответ:

Рис. 3.1.Решение примера 3.1 в Mathcad

3.2. Метод Зейделя

Метод Зейделя является модификацией метода итерации. Он заключается в том, что при вычислении (k+1)-го приближения неизвестного при i>1 используют уже вычисленные ранее (k+1)-е приближения неизвестных

Пусть дана приведенная линейная система

Выберем произвольно начальные приближения корней ,

Далее, предполагая, что k-е приближения корней известны, согласно Зейделю будем строить (k+1)-е приближения корней по следующим формулам:

Процесс повторяется до тех пор, пока разница между двумя соседними приближениями не будет меньше необходимой точности.

Условия сходимости те же, что и для метода итераций.

Пример 3.2. Пусть дана линейная система и приближенные корни системы:

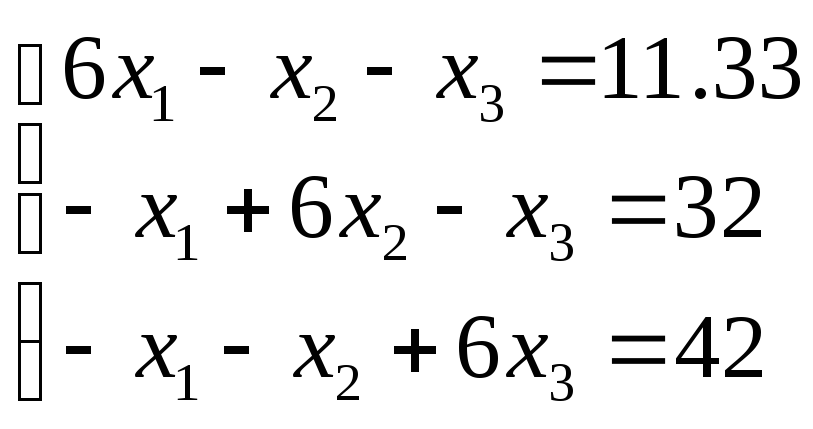и .

Приведем систему к виду, удобному для итераций

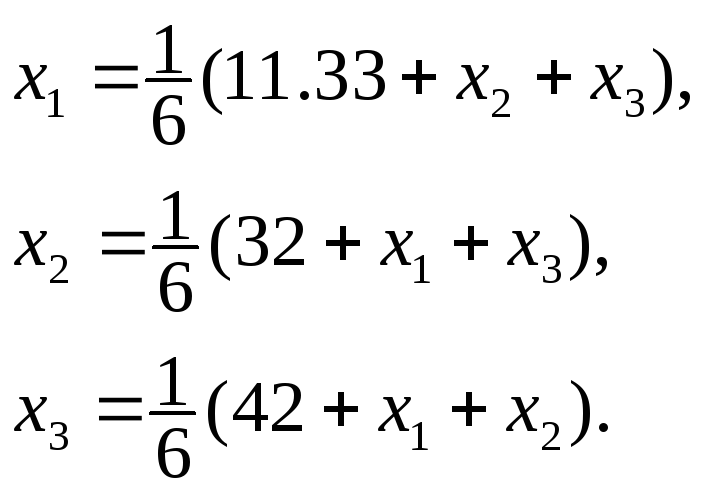
поэтому метод сходится

Взяв в качестве начальных приближений: , получим:

при k=1

при k = 2

Найдем разность по модулю между соседними приближениями:

|-| = 0,00048

|-| = 0,00047

|-| = 0,00016

Так как для приведенной системы выполняется условие сходимости при _,то полученное приближение имеет погрешность, не превышающую 0,0005.

Таким образом, в качестве решения можем принять .