
- •21. 4.1. Передаточная функция и характеристики разомкнутой цепи звеньев
- •4.1.1. Цепь из последовательно соединенных звеньев
- •4.1.2. Цепь из параллельно соединенных звеньев
- •4.1.3. Цепи с местной обратной связью
- •22. Линейные законы регулирования. Понятие о законах регулирования
- •23.Пропорциональное регулирование. Интегральное регулирование. Изодромное регулирование. Регулирование по производным.Пропорциональное регулирование
- •24.Процесс управления и требования к нему. Итд
- •28.Алгебраический критерий устойчивости Гурвица.
- •29. Частотный критерий устойчивости Михайлова
- •Критерий устойчивости Найквиста
- •35. Постановка задач оптимального управления. Фазовые и управляющие переменные. Амплитудные ограничения. Примеры
- •Амплитудные ограничения
- •37. Критерии качества управления. Типы критериев качества
- •38. Классификация задач оптимального управления по типу ограничений фазовые переменные.
- •34.Методы анализа и синтеза систем управления.
- •39. Распространенные задачи оптимального управления. Основные проблемы теории управляемых процессов.
- •40.Принцип максимума л.С. Понтрягина в теории оптимальных систем
- •41.Метод динамического программирования р. Беллмана
- •42. Применение принципа максимума, как проверочного условия
- •43.Применение принципа максимума для сведения задачи оптимального управления к решению двухточечной краевой задачи.
- •45. Принцип максимума л.С. Понтрягина для задач Больца, Лагранжа
- •46. Принцип максимума л.С. Понтрягина для задач терминального управления
- •48. Свойства функции Гамильтона. Достаточность принципа максимума для линейных систем
- •48. Свойства функции Гамильтона. Достаточность принципа максимума для линейных систем
- •31. Области устойчивости сау. Метод корневого годографа. Критерий Вышнеградского. Метод d-разбиения. Области устойчивости сау
- •Метод корневого годографа
- •Критерий Вышнеградского
- •Метод d-разбиения
- •25. Операционный метод расчета переходных процессов в сау. Преобразования Фурье, Лапласа, Карсона-Хевисайда. Теорема разложения Преобразование Лапласа
- •Преобразование Карсона-Хевисайда
- •Теорема разложения
- •Преобразование Фурье
37. Критерии качества управления. Типы критериев качества
управление объектом связано с выбором допустимых управлений.
В соответствии с целью управления для формулировки задачи оптимального управления необходимо определить количественный критерий качества управления.
Необходимо определить некоторый функционал J(u), ставящий в соответствие любому допустимому управлению некоторое число, характеризующее качество этого управления, относительно выбранного функционала. Функционал J есть отображение множества допустимых управлений на действительную прямую
![]()
![]() -функциональное
множество допустимых управлений.
-функциональное
множество допустимых управлений.
Оптимальное
управление доставляет экстремальное
значение критерию качества. В последующем,
без ограничения общности, будем
рассматривать только задачи минимизации.
Оптимальное управление будем обозначать
![]()
![]() .
Оптимальное управление
.
Оптимальное управление
![]() характеризуется соотношением
характеризуется соотношением
![]() ,
,
![]() ,
,
![]() .
.
Допустим,
что задано начальное состояние
![]() .
Тогда решение системы (10.1.2), соответствующее
оптимальному управлению u*(t)
называется оптимальной фазовой
траекторией объекта и обозначается
x*(t),
.
Тогда решение системы (10.1.2), соответствующее
оптимальному управлению u*(t)
называется оптимальной фазовой
траекторией объекта и обозначается
x*(t),
![]() .
.
Наиболее распространенными в теории оптимального управления являются следующие типы функционалов:
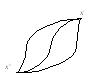 1) Терминальный
функционал (Функционал Майера)
1) Терминальный
функционал (Функционал Майера)
Это некоторый функционал от конечного состояния системы
![]() .
.
2) Функционал задачи быстродействия (функционал быстродействия)
Данный функционал соответствует времени перехода объекта из одного состояния в другое
![]() .
.
Конечный
момент времени
![]() не задан. Нужно перевести систему из
одного состояния в другое за минимальное
время. Здесь имеет место неявная
зависимость функционала от управления.
не задан. Нужно перевести систему из
одного состояния в другое за минимальное
время. Здесь имеет место неявная
зависимость функционала от управления.
3) Функционал интегрального типа (функционал Лагранжа)
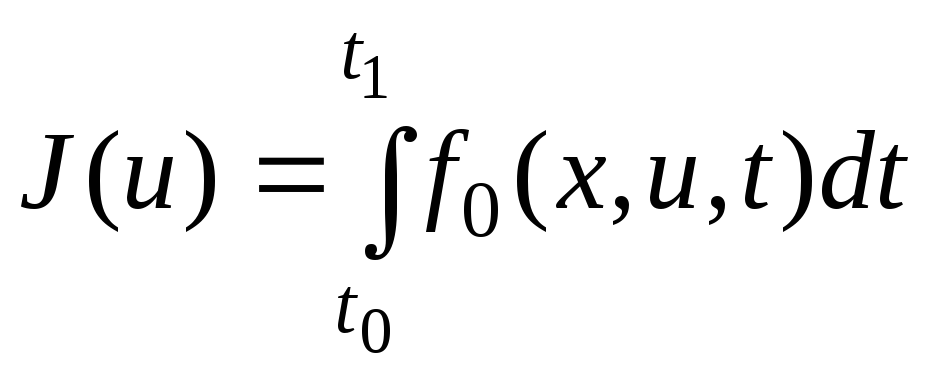 .
.
4) Функционал Больца
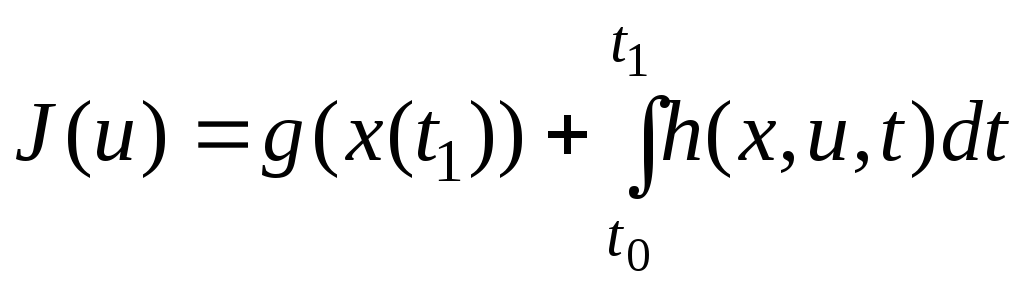 .
.
Это есть комбинация терминального функционала и функционала Лагранжа.
Н ужно
найти управление из числа допустимых,
чтобы функционал имел минимальное
значение.
ужно
найти управление из числа допустимых,
чтобы функционал имел минимальное
значение.
38. Классификация задач оптимального управления по типу ограничений фазовые переменные.
1) Задачи оптимального управления с фиксированным и нефиксированным конечным моментом времени.
Начальный
момент времени
![]() ,
как правило, фиксирован, конечный же
момент времени
,
как правило, фиксирован, конечный же
момент времени
![]() может быть как фиксированным, так и
нефиксированным. Если конечный момент
времени
может быть как фиксированным, так и
нефиксированным. Если конечный момент
времени
![]() фиксирован, то соответствующая задача
оптимального управления называется
задачей с фиксированным временем.
фиксирован, то соответствующая задача
оптимального управления называется
задачей с фиксированным временем.
Если
момент
![]() не фиксирован, то соответствующая задача
оптимального управления называется
задачей с нефиксированным временем.
не фиксирован, то соответствующая задача
оптимального управления называется
задачей с нефиксированным временем.
В
задаче оптимального управления с
нефиксированным временем необходимо
найти оптимальное управление u*(t) и
оптимальный конечный момент времени
![]() ,
которые доставляют минимум выбранному
функционалу.
,
которые доставляют минимум выбранному
функционалу.
Пример задачи с нефиксированным временем – задача быстродействия.
2) Задача оптимального управления с закрепленными концами траекторий.
Зададим
в фазовом пространстве Х две точки:
![]() и
и
![]() .
Задача состоит в том, чтобы перевести
систему из состояния
.
Задача состоит в том, чтобы перевести
систему из состояния
![]() в состояние
в состояние
![]() .
Ограничения налагаются так, что
оптимальное управление должно перевести
объект из точки
.
Ограничения налагаются так, что
оптимальное управление должно перевести
объект из точки
![]() ,
в точку
,
в точку
![]() и доставить минимальное значение
определенному функционалу.
и доставить минимальное значение
определенному функционалу.
Граничные
условия имеют вид:
![]() ,
,
![]() .
.
Рассматриваются всевозможные траектории, соединяющие эти точки.
Из этого множества необходимо выбрать траекторию, которая минимизирует функционал.
Рис. 10.2. Фазовые траектории задачи оптимального управления с закрепленными концами траекторий
3) Задача оптимального управления с подвижными концами фазовых траекторий
В
фазовом пространстве Х задаются два
множества Г1
и Г2:
![]() Ø.
Ø.
Задача
состоит в том, чтобы переместить объект
из множества Г1:
![]() ,
на множество Г2:
,
на множество Г2:
![]() и минимизировать при этом функционал.
и минимизировать при этом функционал.
Среди бесконечного множества траекторий выбирается та, которая минимизирует функционал.
Рис. 10.3. Фазовые траектории задачи оптимального управления
с подвижными концами траекторий
Как правило, начальный момент и начальные условия задаются.
4) Задача оптимального управления с подвижным правым концом фазовой траектории
![]() .
.
Множество
![]() в этом случае вырождается в точку.
в этом случае вырождается в точку.
5) Задача оптимального управления со свободным правым концом фазовой траектории.
В этом случае на правый конец фазовой траектории никаких ограничений не задается. Необходимо минимизировать функционал при заданном начальном условии.
6) Задача оптимального управления с ограничениями на фазовые переменные.
Ограничения
задаются не только на концы фазовой
траектории, но и на траекторию в целом.
В фазовом пространстве Х задается
множество Г(t),
![]() ,
и фазовая траектория не должна выходить
за пределы этого множества:
,
и фазовая траектория не должна выходить
за пределы этого множества:
![]() ,
,
![]() .
.
Пример.
![]() ,
,
![]()
