. Свободные колебания полубесконечной струны (стержня)

Соответствующая краевая задача для струны с жестко закрепленным краем имеет вид:

Введём функции:

получающиеся нечетным продолжением начальных условий через точку х=0.

Тогда краевая задача сводится к уже рассмотренной ранее:

Проверим выполнимость начальных и краевых условий.

_,

_.

Поскольку производная от интеграла

имеет вид

_{, получаем}

_.

При х=0 получаем

Получили решение краевой задачи (2.7а) в области 0≤х<∞ в виде (2.6) при нечетном продолжении начальных условий.

Рассмотрим теперь краевую задачу:

Начальные условия четным образом продолжим через х=0:

_.

Эта краевая задача тоже сводится к уже рассмотренной:

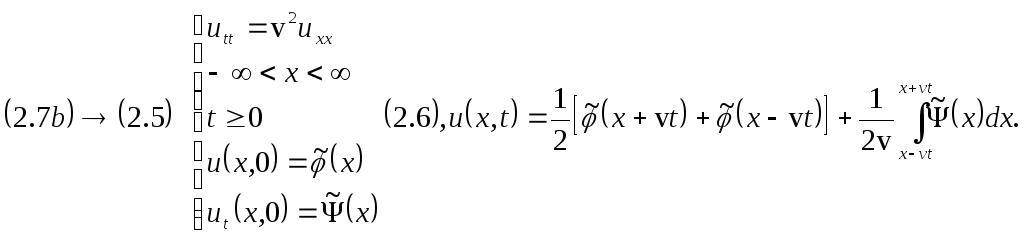
Теперь проверяем выполнимость начальных и краевых условий:

,

,

.

Для вычисления u_x(x,t) воспользуемся правилом дифференцируемости интегралов

,

_.

Получаем

,

_.

Получили решение краевой задачи (2.7б) при четном продолжении начальных условий.

. Свободные колебания струны ограниченных размеров

В этом случае при закрепленном при х=0 конце струны краевая задача имеет вид:

Продолжаем функции нечетным образом с периодом 2l черех х=0 и х=l.

Покажем, что (2.6) является решением задачи (2.8). Ясно, что .

Проверим выполнение начальных и краевых условий.

Начальные условия:

,

,

_.

Краевые условия:

_,

Начальные условия продолжим четным образом через х=0 и х=l.

_{и т.д.}

2.80 Вынужденные колебания бесконечной струны

Сформулируем задачу для вынужденных колебаний бесконечной струны с внешним воздействием:

(2.8) .

Используем метод редукции представим решение в виде суммы

. Разбиваем краевую задачу (2.8) на 2 части.

_{(2.8а) (2.8б)}

Решение (2.8а) есть решение (2.5). Тогда получаем:

.

Представим u⁽²⁾(x,t)=

Лемма:

u⁽²⁾ есть решение (2.8б), если z(x,t,τ) является решением (2.8в):

(2.8в)

Доказательство:

u_хх⁽²⁾(x,t)=

u_t⁽²⁾= .

Воспользуемся формулой интегрирования интеграла, зависящего от параметра, и получим:

u_tt⁽²⁾= .

u_tt⁽²⁾-v²u_xx⁽²⁾= - v² =f(x,t).

Лемма доказана.

Введем обозначение ==, где s=t-τ. Тогда

(2.8в)

(2.8в) переходит в (2.5) при переобозначениях t→s, φ(x)→0, ψ(x)→f(x,τ).

Поэтому решение(2.8в) можно построить через формулу Даламбера

(2.6) .

z(x,s)= . Тогда

u⁽²⁾(x,t)= .

Получаем решение краевой задачи (2.8).

(2.9) .

Выражение (2.9) при f(x,t)=0 переходит в решение в виде формулы Даламбера (2.6).

28