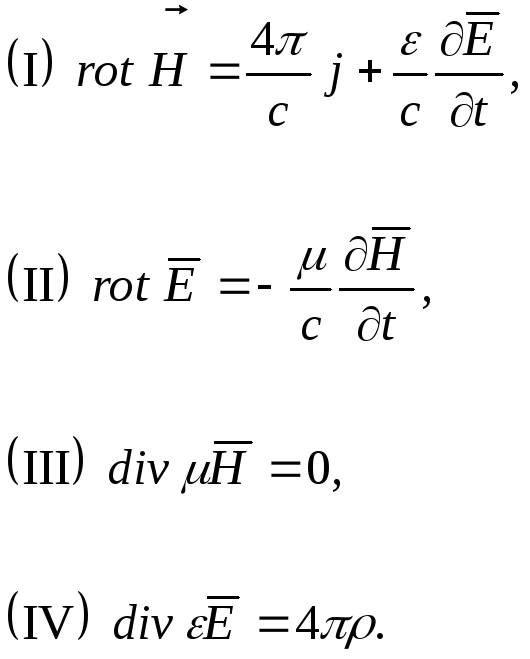- •Тема 2. Уравнения гиперболического типа . Уравнения малых поперечных колебаний упругой струны.
- •. Малые продольные колебания упругого стержня
- •.Малые поперечные колебания упругой мембраны
- •2.4º Электромагнитное поле в однородных средах
- •. Постановка краевых задач и их редукция.
- •. Свободные колебания бесконечной струны (стержня)
- •. Свободные колебания полубесконечной струны (стержня)
- •. Свободные колебания струны ограниченных размеров
- •2.80 Вынужденные колебания бесконечной струны
.Малые поперечные колебания упругой мембраны
Под
мембраной будем понимать поверхность
![]() ,
опирающуюся на замкнутый контур
,
опирающуюся на замкнутый контур
![]() .
.
Введём некоторые ограничения:
![]() ,
где v-
скорость точки мембраны.
,
где v-
скорость точки мембраны.
Точки мембраны колеблются перпендикулярно плоскости, в которой она находится в положении равновесия.
![]() –
отклонение
от положения равновесия точки с
координатами
–
отклонение
от положения равновесия точки с
координатами
![]() в момент времени
в момент времени
![]() .
Скорость
.
Скорость ![]() перпендикулярна плоскости (х,у). Таким
образом, любое сечение перпендикулярно
плоскости
перпендикулярна плоскости (х,у). Таким
образом, любое сечение перпендикулярно
плоскости
![]() и для него может быть построена задача,
аналогичная 2.1º
и для него может быть построена задача,
аналогичная 2.1º
б) Будем считать мембрану гибкой, т.е. силы натяжения направлены по касательной к мгновенному профилю.
![]() .
.
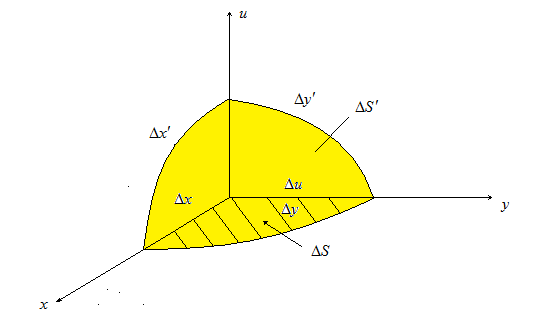
Введём линейную плотность силы.
![]() .
.
![]() Колебания
малы и происходят без растяжения
мембраны:
Колебания
малы и происходят без растяжения
мембраны:
![]()
![]() ,
что дает:
,
что дает:
![]() .
.
Возьмём
направление
![]() ,
в котором мембрана имеет наиболее крутой
наклон и рассечём мембрану в этом
направлении.
,
в котором мембрана имеет наиболее крутой
наклон и рассечём мембрану в этом
направлении.
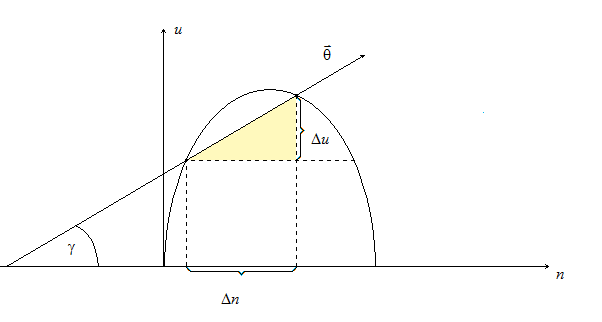
![]() максимальный
угол наклона касательной к оси х.
максимальный
угол наклона касательной к оси х.
![]() .
.
Градиент u направлен в сторону наибольшего возрастания функции U.
Проекции
![]() равны
равны
|
|
, |
![]() ,
тогда
,
тогда
![]() .
.
Производная остаётся постоянной и не зависит от времени.
![]() Участок
мембраны при колебаниях не сдвигается
в плоскости
Участок
мембраны при колебаниях не сдвигается
в плоскости
![]() за время
за время
![]() .
Пусть
.
Пусть
![]() за
время
за
время
![]()
![]() за
время
за
время
![]() .
Получаем
.
Получаем
![]() условие
отсутствия сдвига.
условие
отсутствия сдвига.
![]() .
.
Если равны интегралы по произвольной области, то равны подынтегральные выражения.
![]() и
и
![]() не зависит от
не зависит от
![]() .
.
Аналогично
![]()
![]() ,
,
![]() не зависит от
не зависит от
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Введем
поверхностную плотность массы. Пусть
![]() малый элемент мембраны и
малый элемент мембраны и
![]() масса мембраны, тогда
масса мембраны, тогда
![]() .
.
Используем второй закон Ньютона
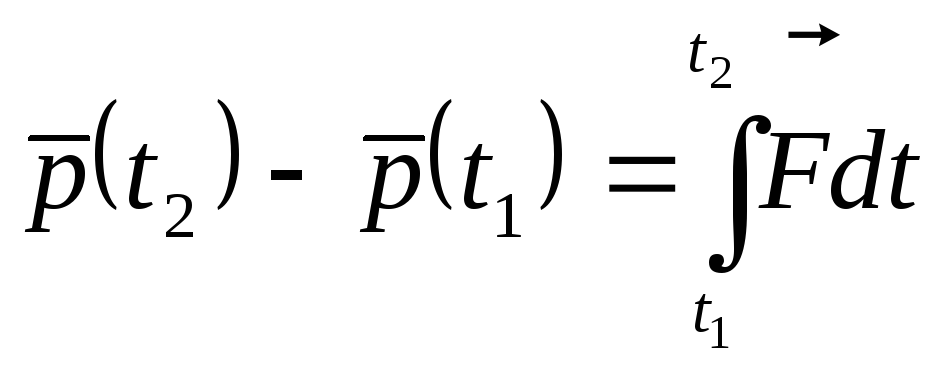 ,
,
![]() .
.
Для
малого элемента мембраны dS
:
![]() ,
d
,
d![]() =
=![]() .
.
Для
конечного по размерам участка
![]() ,
,
![]() .
.
Получаем
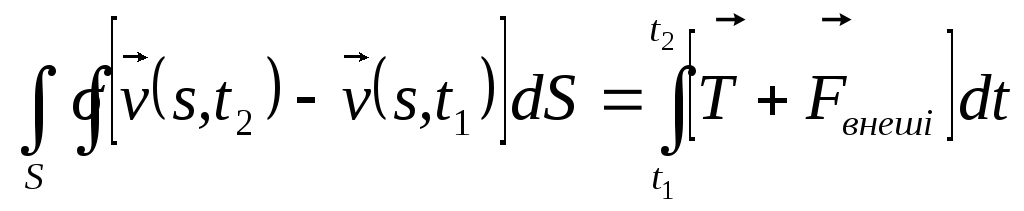 .
.
Введем поверхностную плотность внешней силы
![]() ,
,
![]() ,
,
![]() ,
тогда второй закон Ньютона перепишется
в виде
,
тогда второй закон Ньютона перепишется
в виде
 .
.
Проектируем
на ось
![]()
![]() ,
,
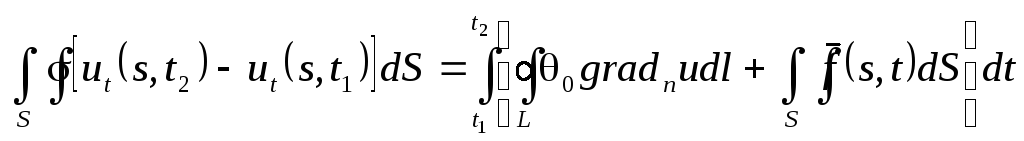 .
.
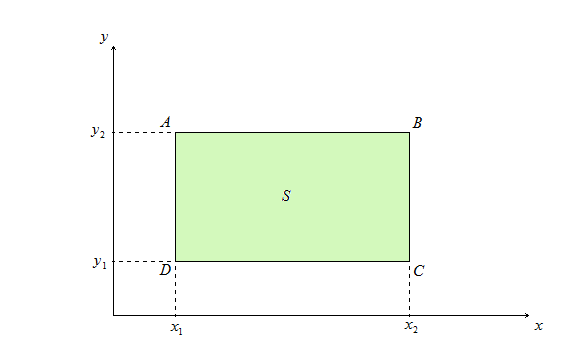
Теорема Остроградского – Гаусса имеет вид в двумерном случае
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() ;
;
![]() .
В нашем случае
.
В нашем случае
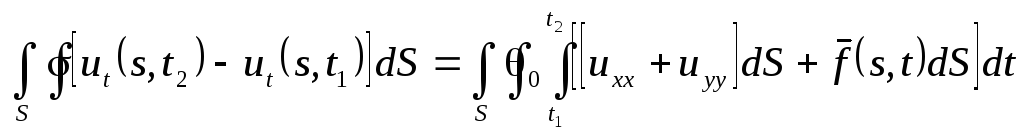 .
.
Имеем интегральное равенство для произвольных областей, следовательно, равны подынтегральные выражения.
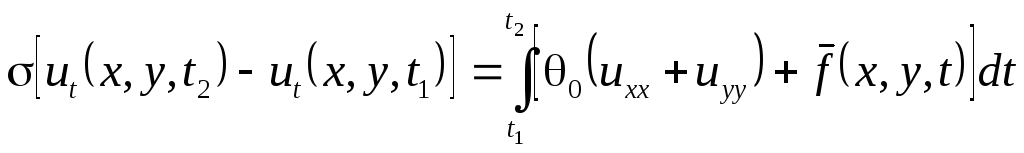 .
.
Воспользуемся теоремой о среднем:
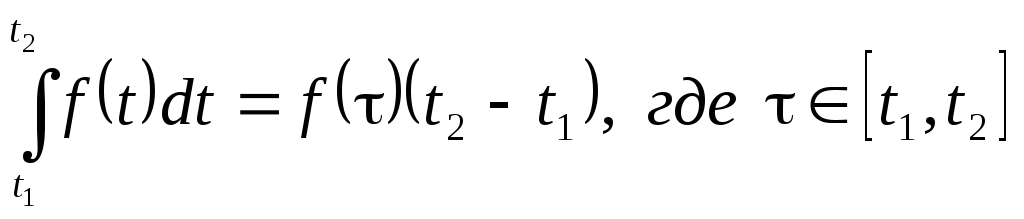 ,
и получим
,
и получим
![]() .
.
После предельного перехода
![]()
получаем
![]() ,
,
![]()
В отличии от одномерных задач (2.1) и (2.2) уравнение (2.3) является двумерным.
Проверяем
размерность ![]() :
:
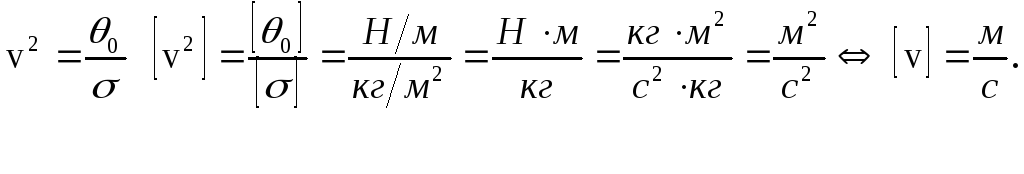
2.4º Электромагнитное поле в однородных средах
Запишем уравнения Максвелла в произвольной среде.
|
|
В однородной среде:
|
В
вакууме
![]()
Запишем уравнения Максвелла в изотропной среде(λ,μ,ε- постоянны):
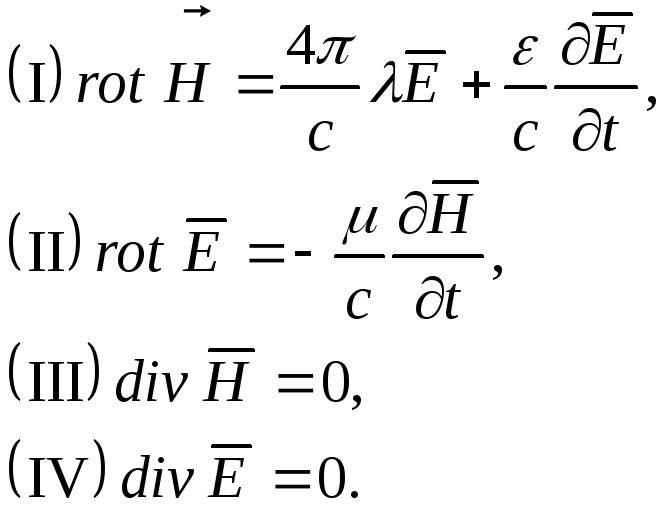
Известно векторное равенство
rot
rot
![]() =
grad
div
=
grad
div
![]() - ∆
- ∆ ![]() .
.
Действуем операцией rot на первое уравнение.
![]()
![]()
Так
как
![]() ,
то
,
то
![]() ,
,
![]() .
.
Действуем операцией rot на второе уравнение.
![]() ,
,
![]() .
.
Так
как
![]() ,
то
,
то
![]() .
Получаем 6 уравнений для компонент
векторов напряженности.
.
Получаем 6 уравнений для компонент
векторов напряженности.
![]()
![]()
![]()
Введем полевую функцию
![]() ,
для которой
,
для которой
![]() ,
,
![]()
Уравнение
(2.4) – уравнение гиперболического типа,
в соответствии с 1.6º , причем
-
![]() – поглощение электромагнитным полем
энергии.
– поглощение электромагнитным полем
энергии.
В одномерном случае уравнение принимает вид:
![]()