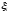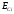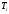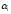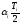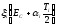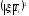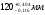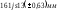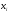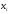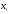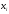Расчет линейных размерных цепей вероятностным методом. Обратная задача.

Найти предельные значения замыкающего размера 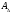при значениях составляющих размеров, полученных в результате решения прямой задачи. Допустимый процент брака на сборке равен 0,27%

Сведем данные для расчета в таблицу

Обозначение размера	Размер
А1	21-0,12 мм	+1	-0,06	0,12	+0,2	0,012	-0,048	-0,048	0,0144
А2		+1	0,144	0,52	+0,2	0,052	0,196	0,196	0,2704
А3	21-0,12 мм	+1	-0,06	0,12	+0,2	0,012	-0,048	-0,048	0,0144
А4		-1	0	0,63	0	0	0	0	0,3969

1. Номинальное значение замыкающего размера

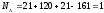
2. Среднее отклонение замыкающего размера

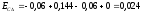
3. Допуск замыкающего размера

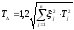
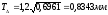
4. Предельные отклонения замыкающего размера

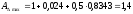
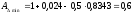
5. Сравниваем полученные результаты с заданными

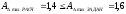
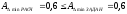
Следовательно, изменения предельных отклонений составляющих размеров не требуется.

Часть 3

Обработка результатов многократных измерений.

Доверительная вероятность P=0,98

15.96 15.50 15.75 15.65 15.68 15.49 15.71 15.57 15.68 15.49 15.38 15.77 15.62 15.65

15.59 15.56 15.35 15.93 15.83 15.67 15.68 15.25 15.47 15.76 15.47 15.61 15.69 15.56

15.61 15.74 15.56 15.31 15.80 15.46 15.35 15.77 15.50 15.80 15.80 15.78 15.82 15.34

15.48 15.67 15.57 15.42 15.61 15.55 15.67 15.58 15.68 15.80 15.54 15.88 15.62 15.50

15.64 15.58 15.67 15.58 15.73 15.73 15.48 15.52 15.72 15.59 15.60 15.68 15.48 15.62

15.47 16.00 15.52 15.65 15.53 15.74 15.60 15.48 15.43 15.82 15.79 15.53 15.58 15.57

15.53 15.49 15.40 15.53 15.51 15.69 15.75 15.34 15.67 15.43 15.43 15.63 15.81 15.49

15.68 15.62

1. Определяем среднее арифметическое и стандартное отклонение.

Среднее арифметическое является статической оценкой математического ожидания для ряда однородных результатов.

.

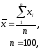
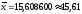Стандартное отклонение является статической оценкой среднего квадратического отклонения.

.

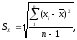
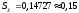2. С помощью правила «трех сигм» проверяем наличие или отсутствие грубых промахов.

,

.

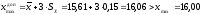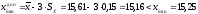Получаем, что 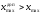и 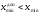. Таким образом, ни один из результатов не выходит за границы интервала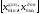, следовательно, с вероятностью 0,9973 гипотеза об отсутствии грубых погрешностей принимается.

3. Построение гистограммы и выдвижение гипотезы о виде закона распределения вероятности.

Для построения гистограммы, необходимо результаты отдельных измерений расположить в так называемый вариационный ряд по возрастанию их численных значений.

Таблица 1

	15,25	15,31	15,34	15,35	15,38	15,40	15,42	15,43	15,46	15,47	15,48	15,49	15,50
Кол-во	1	1	2	2	1	1	1	3	1	3	4	4	3
	15,51	15,52	15,53	15,54	15,55	15,56	15,57	15,58	15,59	15,60	15,61	15,62	15,63
Кол-во	1	2	4	1	1	3	3	4	2	2	3	4	1
	15,64	15,65	15,67	15,68	15,69	15,71	15,72	15,73	15,74	15,75	15,76	15,77	15,78
Кол-во	1	3	5	6	2	1	1	2	2	2	1	2	1
	15,79	15,80	15,81	15,82	15,83	15,88	15,93	15,96	16,00
Кол-во	1	4	1	2	1	1	1	1	1

Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разбивается на k=9 одинаковых интервалов .

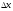Ширину интервала определим по формуле:

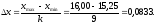
Выбираем начало первого интервала так, чтобы его значение оказалось меньше минимального результата вариационного ряда, а последний интервал покрывал бы максимальное значение ряда. Примем начало первого интервала в точке 15,20 , тогда конец последнего (10-го) интервала окажется в точке 16,033.

Подсчитаем для каждого интервала количество результатов 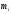, попавших в каждый отдельный интервал, используя формулу:

.

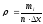Учтем что, если в интервал попадает меньше пяти наблюдений, то такие интервалы необходимо объединить с соседними, соответственно изменяя и параметр 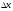. Так объединим в один первые два интервала, а также два последних интервала. Общее число интервалов станет равным 6.

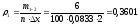
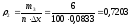
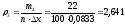
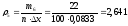
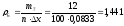
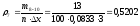
Результаты производимых вычислений занесем в таблицу 2 (см. прил. 2), а затем построим саму гистограмму (см. прил. 1).

Из вида гистограммы на рис.1 можно сделать предположение о том, что вероятность результата измерения подчиняется нормальному закону. Проверим правдивость этой гипотезы.

4. Для проверки нормальности закона применим критерий Пирсона.

Если выдвинута гипотеза о нормальности распределения, то для расчета вероятностей используем функцию Лапласа:

,

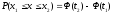где 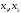– значения соответствующие началу и концу интервала.

Для каждого из этих значений рассчитаем относительный доверительный интервал t по формуле:

.

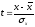Затем из таблиц Лапласа найдем соответствующие значения функци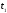й Ф() и Ф(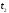). При этом будем иметь в виду, что конец предыдущего интервала является началом последующего.

Произведем численный расчет.

первый интервал:

,

.

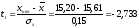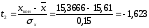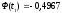
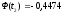
второй интервал:

,

.

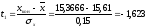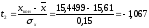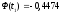
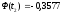
третий интервал:

,

.

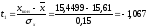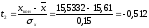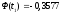
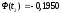
четвертый интервал:

,

.

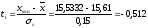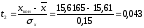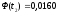
пятый интервал:

,

.

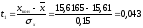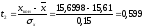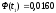
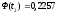
шестой интервал:

,

.

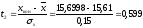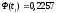
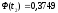
седьмой интервал:

,

.

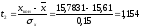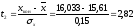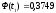
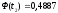
На основании вычисленных значений функции Лапласа получаем:

Рассчитанные значения 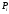занесем в таблицу 2 и на их основе произведем расчет значений 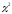- критерия для каждого интервала.

Значения критерия для отдельного интервала рассчитаем по формуле:

,

где n – общее количество проведенных измерений,

m – число результатов измерений, попавших в данный интервал.

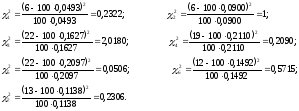
Суммарное значение критерия определим по формуле:

.

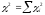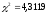
Определим табличное (критическое) значени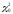е - критерия, задавшись доверительной вероятностью 0,95 и вычислив число степеней свободы по формуле:

,

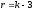где k – число интервалов.

Получаем:

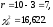
Т.к. 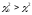, следовательно, с вероятностью 0,98 гипотеза о нормальности распределения вероятности результата измерения принимается.

5. Строим теоретическую кривую плотности вероятности.

Её следует строить в тех же координатах, что и гистограмму. Для этого рассчитаем значения плотности вероятности для середины каждого интервала по формуле:

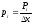
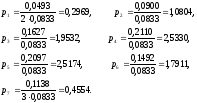
6. Представление результата в виде доверительного интервала.

Определим стандартное отклонение среднего арифметического 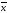по формуле:

.

.

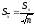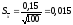Закон распределения вероятности для среднего арифметического считаем нормальным (что следует из нормальности распределения самой измеряемой величины), тогда доверительный интервал определяется по формуле:

,

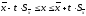где t – параметр, который находится в зависимости от заданной доверительной вероятности. Доверительной вероятности 0,98 соответствует аргумент функции Лапласа .

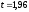Окончательно получим:

,

.

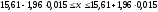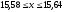Рассмотрим случай, когда закон распределения вероятности для среднего арифметического считается неизвестным, тогда относительный доверительный интервал рассчитывается в соответствии с неравенством Чебышева:

.

,

.

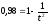
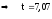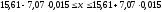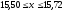Как видно из сравнения результатов, неизвестность закона распределения вероятности приводит к расширению доверительного интервала, то есть к увеличению дефицита измерительной информации.