Теорема Коши для односвязной области
Пусть
− односвязная область,
− любой кусочно-гладкий замкнутый
контур, лежащий в области
.
Если
функция
является аналитической в области
и на самом контуре, то интеграл по
замкнутому контуру равен нулю:
.
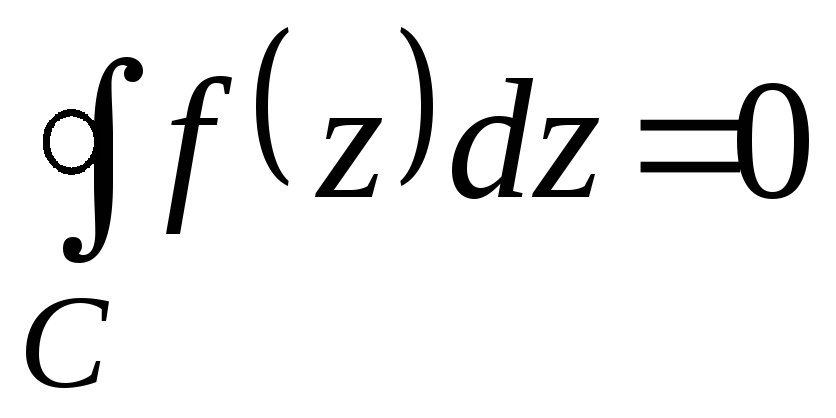(16)
Справедлива и обратная теорема – теорема Морера.
Теорема Морера
Пусть однозначная
функция
непрерывна в односвязной области
и интеграл по любому замкнутому контуру,
лежащему в области
от функции
,
равен нулю, тогда функция
является аналитической функцией.
Если область
замкнутая односвязная область, функция
аналитическая в этой области, то в
качестве замкнутого контура можно взять
границу области
.
Рассмотрим
обобщение данной теоремы Коши на
многосвязные
области,
ограниченные не самопересекающимися
контуром
и
простыми замкнутыми контурами
,
лежащими внутри общего контура
и вне друг друга.
Теорема Коши для −связной области
Пусть функция
аналитическая в
−связной
области
,
тогда интеграл от функции по всем
границам равен нулю, при этом предполагается,
что обход граничных кривых происходит
в положительном направлении.
Рис. 6
Доказательство
Разрезают область
дугами
и
.
Из области
получают односвязную область
(см. рис. 6).
Для нее по теореме об односвязной области получают:
,
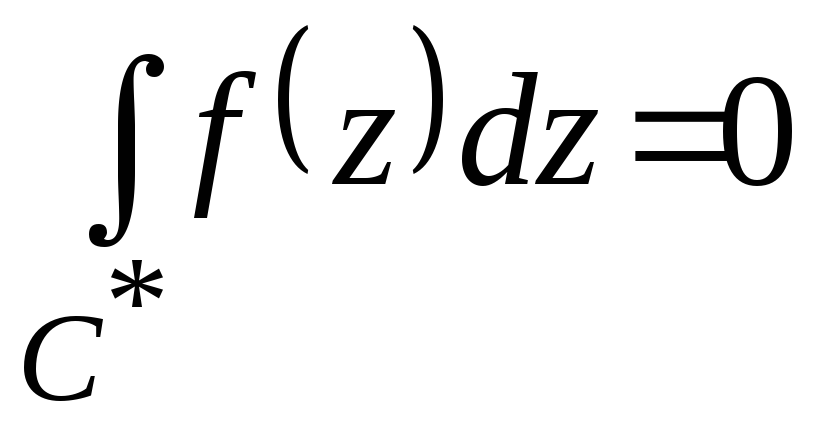где
− граница односвязной области
.
При обходе по общей
границе
контуры
,
,
проходят в положительном направлении
один раз. Дуги
и
проходят два раза в положительном и
отрицательном направлении:
,
где
и
.
В итоге
.
Следствия теоремы Коши для −связной области
-
При выполнении условий теоремы интеграл по внешнему контуру равен сумме интегралов по внутренним (обход на всех контурах в одну сторону (см. рис. 6)):
.
2. Если функция
является аналитической в односвязной
области 
и на границе области, за исключением,
быть может, некоторой точки
этой области, то интегралы от функции
по различным замкнутым кривым, которые
лежат в области
и ограничивают области, содержащие
точку
,
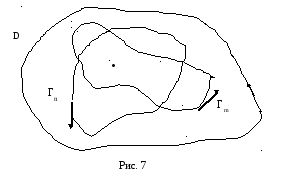
равны между собой (см. рис. 7):
.
Точки, в которых
однозначная функция
является аналитической, называются
регулярными
или правильными.
Особыми точками
функции
называют точки, в которых функция не
является аналитической или неопределенна.
изолированной
особой точкой
называется точка, для которой существует
такая окрестность, что функция
является аналитической во всех точках
этой окрестности кроме самой точки.
Интегральная формула Коши
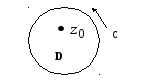
Рис. 8
Пусть
функция
является аналитической функцией в
некоторой замкнутой области
(односвязной или
-связной)
и на еë границе. Кривая
,
ограничивающая контур, является
кусочно-гладкой. Значение функции в
любой внутренней точке
области
(рис. 8)
будет определяться по формуле
.
(17)
Эта формула выражает
фундаментальное свойство аналитических
функций: аналитическая
функция
в замкнутой области
вполне определяется своими значениями
на границе этой области.
Формально для
любой подынтегральной функции
,
имеющей в замкнутой области особую
точку
,
необходимо преобразовать вид функции,
выделив в знаменатель выражение
.
Остальную часть функции необходимо
записать в числитель
.
Полученная в числителе функция
станет аналитической в рассматриваемой
области.
Формула (17) позволяет вычислять контурные интегралы вида
.
(18)