18. Эмпирическая функция распределения.

Пусть известно статистическое распределение частот количественного признака X. Введем обозначения:

mx- число наблюдений, при которых наблюдалось значение признака, меньшее х; п- общее число наблюдений (объем выборки). Ясно, что относительная частота события Х < х равна. mx/n. Если х изменяется, то изменяется и относительная частота, т. е. относительная частота есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию определяющую для каждого значения х относительную частоту события Х < х, т.е.

В отличие от эмпирической функции распределения выборки функцию распределения F (х) генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F (х) определяет вероятность события Х < х, а эмпирическая функция определяет относительную частоту этого же события. Из теоремы Бернулли следует, что относительная частота события Х < х, т. е. эмпирическая функция стремится по вероятности к вероятности F (х) этого события. Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности.

Эмпирическая функция обладает всеми свойствами F(x):

1) ее значения принадлежат отрезку [0, 1];

2) неубывающая;

3) если хi -наименьшая варианта, то

если x k - наибольшая варианта, то

Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

17.

Вариационным рядом называется последовательность вариантов запис-х в возрастном порядке и соответ-х им частот.Число показывающее сколько раз повторяется в данной со-ти каждой называется частотой.

Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную ее величину и непрерывным, если его значения могут отличаться одно от другого на сколько угодно малую величину.

Графическое изображение

• Полигон частот –называют ломанную, отрезки которой соед-т точки (х1;m1),(x2;m2)….(Xk;Wk),где Хi-варианты выборки,Wi-соответствующие им относительные частоты(относительные частоты выч-ся по формуле Wi=mi/n)

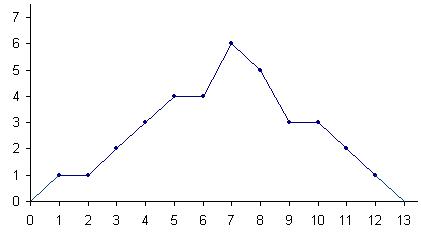
• Гистограмма- служит для изображения интервальных вариац-х рядов и представляет собой ступенчатую фигуру из прямоугольников с основанием= интервальным значением признака(Хi-1;Xi)и высотами= частотам mi интервалов.

• Кумулята служит для графического изображения кумулятивного вариационного ряда. Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат - накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты - соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой.

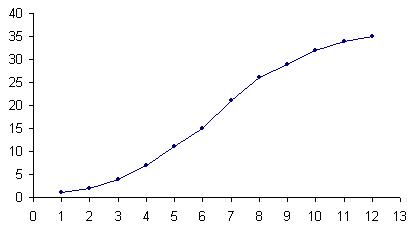
• Огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.

Разновидностью кумуляты является кривая концентрации или график Лоренца. Для построения кривой концентрации на обе оси прямоугольной системы координат наносится масштабная шкала в процентах от 0 до 100. При этом на оси абсцисс указывают накопленные частости, а на оси ординат — накопленные значения доли (в процентах) по объему признака.

Равномерному распределению признака соответствует на графике диагональ квадрата . При неравномерном распределении график представляет собой вогнутую кривую в зависимости от уровня концентрации признака.

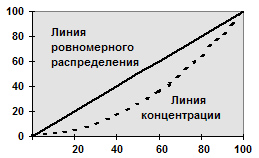
16.При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные.

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

На практике обычно пользуются бесповторным случайным отбором.

Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной) .

В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.

№19) Понятие точечной и интервальной оценок неизвестных параметров распределения и их свойства.

Понятие о точечной оценке

Выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики, называется ее точечной статистической оценкой. Их недостаток заключается в том, что неизвестно, с какой точностью оценивается параметр. Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку называют точечной. Точечные оценки могут быть получены с использованием метода моментов, метода максимального правдоподобия и метода наименьших квадратов.

Понятие об интервальных оценках

Если для выборок большого объема точность обычно бывает достаточной (при условии несмещенности, эффективности и состоятельности оценок), то для выборок небольшого объема вопрос точности оценок становится очень важным. Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.

Свойства оценок:

1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

В противном случае оценка называется смещенной и допускает систематическую ошибку. Так, рассмотренное ранее среднее выборочное является несмещенной оценкой среднего генерального. В то же время выборочная дисперсия - является смещенной оценкой генеральной дисперсии.

2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:

Это условие будет выполняться, если и оценка является несмещенной.

3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной:

- Такая оценка называется эффективной.

№20) Требования предъявляемые к оценкам параметров

Оценивая параметр a по выборке, находим такую величину , которую принимаем за точечную оценку параметра a. Естественно, при этом стремимся, чтобы оценка была в определенном смысле наилучшей, поэтому к ней предъявляется ряд требований:

1) Состоятельность. Точечная оценка называется состоятельной, если при неограниченном увеличении объема выборки () она стремится к истинному значению параметра a.

В математической статистике показывается, что состоятельной оценкой генерального среднего значения , является выборочное среднее арифметическое , а состоятельной оценкой генеральной дисперсии — выборочная дисперсия .

2. Несмещенность. Оценка 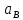называется несмещенной, если она не содержит систематической ошибки, т. е. среднее значение оценки, определенное по многократно повторенной выборке объема n из одной и той же генеральной совокупности, стремится к истинному значению соответствующего генерального параметра a.

Выборочное среднее арифметическое является несмещенной оценкой генерального среднего . Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия, вычисляемая по формуле:

для не сгруппированных данных, для сгруппированных данных.

3. Эффективность. Несмещенная оценка является эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками того же параметра генеральной совокупности.

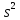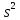Это надо понимать так: полученные по выборке оценки и — случайные величины, так как случайны сами выборочные значения. Поэтому можно говорить о математическом ожидании и дисперсии оценок и Эффективность этих оценок означает, что их дисперсии D() и D(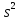) меньше дисперсий любых других несмещенных оценок среднего значения и дисперсии генеральной совокупности.

Итак, наилучшими в указанном смысле оценками генерального среднего значения и генеральной дисперсии являются выборочные характеристики, и .
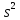