5.4. Обобщение: отсечение двумерного отрезка выпуклым окном

В описанных выше алгоритмах предполагалось, что отсекающее окно является координатно-ориентированным прямоугольником. Однако во многих случаях окно не таково. Кирус и Бек предложили алгоритм отсечения окном произвольной выпуклой формы.

Прежде чем описывать алгоритм Кируса-Бека рассмотрим отсечение параметрически заданного отрезка прямоугольным окном. Параметрическое уравнение отрезка P₁P₂ имеет вид:

P(t)=P₁+(P₂– P₁)t, 0≤t≤1, (1)

где t – параметр. Параметрическое описание отрезка не зависит от выбора системы координат. Это свойство делает параметрическое представление особенно полезным для определения пересечения отрезка со стороной произвольного выпуклого многоугольника.

В двумерной декартовой системе координат уравнение (1) сводится к паре одномерных параметрических уравнений вида:

0≤t≤1. (2)

x(t)=x₁+(x₂– x₁)t,

y(t)=y₁+(y₂– y₁)t,

В случае прямоугольного отсекающего окна одна из координат пересечения отрезка с каждой стороной известна. Необходимо вычислить только вторую координату. Из уравнения (1) получаем:

t=(P(t)–P1)/(P2– P1).

А из уравнения (2) следует, что значения t, соответствующие пересечениям со сторонами окна, равны:

• для левой стороны t=(x_л–x₁)/(x₂–x₁), 0≤t≤1,

• для правой стороны t=(x_п–x₁)/(x₂–x₁), 0≤t≤1,

• для нижней стороны t=(y_н–y₁)/(y₂–y₁), 0≤t≤1,

• для верхней стороны t=(y_в–y₁)/(y₂–y₁), 0≤t≤1.

Здесь через x_л, x_п, y_н, y_в обозначены координаты левой, правой, нижней и верхней сторон окна. Если решения этих уравнений дают значение t за пределами интервала 0≤t≤1, то такие решения отбрасываются, поскольку они соответствуют точкам, лежащим вне заданного отрезка.

5.5. Алгоритм Кируса–Бека

Для создания надежного алгоритма отсечения необходим хороший метод определения местоположения относительно окна (внутри, на границе, вне его) точки, принадлежащей отрезку. Для этой цели в алгоритме Кируса–Бека используется вектор нормали (рис.13).

Возьмем выпуклую отсекающую область R. Доказано, что внутренняя нормаль n в произвольной точке a, лежащей на границе R, удовлетворяет условию:

n(b–a)≥0, (3)

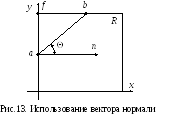
где b – любая точка на границе R, т.к. cos Q всегда положителен.

Возвращаясь к определению пересечения отрезка со стороной окна, вновь возьмем параметрическое представление отрезка P1P2 уравнением (1). Если f – граничная точка выпуклой области R, а n – внутренняя нормаль к одной из ограничивающих эту область плоскостей, то для любой конкретной величины t, т.е. для любой точки отрезка P1P2, из условия n(P(t)–f)<0 следует, что вектор P(t)–f направлен вовне области R. Из условия n(P(t)–f)<0 следует, что вектор P(t)–f принадлежит плоскости, которая проходит через f и перпендикулярна нормали. Из условия n(P(t)–f)>0 следует, что вектор направлен внутрь R. Из всех этих условий, взятых вместе, следует, что бесконечная прямая пересекает замкнутую выпуклую область в двух точках. Далее, пусть эти две точки не принадлежат одной граничной плоскости или ребру. Тогда уравнение n(P(t)–f)=0 имеет только одно решение. Если точка f лежит на той граничной плоскости или ребре, для которых n является внутренней нормалью, то точка на отрезке P(t) будет точка пересечения этого отрезка с указанной граничной плоскостью.

Таким образом запишем формализованный алгоритм Кируса–Бека:

P(t)=P₁+(P₂–P₁)t, 0≤t≤1, (4)

n_i(P(t)–f_i), i=1, 2, 3,… (5)

Решение уравнения будет положительно, равно нулю или отрицательно - в зависимости от того, будет ли избранная точка отрезка лежать с внутренней стороны границы, на самой границе или с ее внешней стороны. Подстановка (4) в (5) дает условие пересечения отрезка с границей области:

n_i(P₁+(P₂–P₁)t–f_i)=0 или n_i(P₁-f_i) + n_i(P₂-P₁)t = 0.

Вектор (P₂–P₁) определяет ориентацию отрезка, а вектор (P₁–f_i) пропорционален расстоянию от первого конца отрезка до избранной граничной точки. Обозначим через D=P₂–P₁ директрису или ориентацию отрезка, а через W_i=P₁–f_i - некий весовой множитель. Тогда получаем уравнение:

t(n_i*D)+W_i*n_i=0

Если W_i*n_i<0, то эта точка вне окна. Если W_i*n_i=0, то эта точка на границе. Если W_i*n_i>0, то эта точка внутри окна. Последнее уравнение используется для получения значений t соответствующих пересечениям отрезка с каждой стороной окна. Если значение t лежит за пределом интервала 0≤t≤1, то оно игнорируется.