
- •Контрольные варианты к задаче 1
- •Контрольные варианты к задаче 2
- •Контрольные варианты к задаче 3
- •Контрольные варианты к задаче 4
- •Контрольные варианты к задаче 5
- •Контрольные варианты к задаче 6
- •Контрольные варианты к задаче 7
- •Контрольные варианты к задаче 8
- •Контрольные варианты к задаче 9
- •Контрольные варианты к задаче 10
- •Контрольные варианты к задаче 11
- •Контрольные варианты к задаче 12
- •Контрольные варианты к задаче 13
- •Контрольные варианты к задаче 14
- •Контрольные варианты к задаче 15
- •Контрольные варианты к задаче 16
- •Контрольные варианты к задаче 17
- •Контрольные варианты к задаче 18
- •Контрольные варианты к задаче 19
- •Контрольные варианты к задаче 20
- •Контрольные варианты к задаче 21
- •Контрольные варианты к задаче 22
- •Контрольные варианты задачи 23
- •Контрольные варианты задачи 25
- •Контрольные варианты задачи 26
- •Библиографический список
Контрольные варианты к задаче 20
Вычислить пределы функций:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
26. |
|
|
27. |
|
28. |
|
|
29. |
|
30. |
|
З а д а ч а 21
Пример 23
Вычислить
![]() .
Это неопределенность вида
.
Это неопределенность вида
![]() .
.
Так
как
![]() .
.
Найдем, используя свойство непрерывности логарифмической функции:
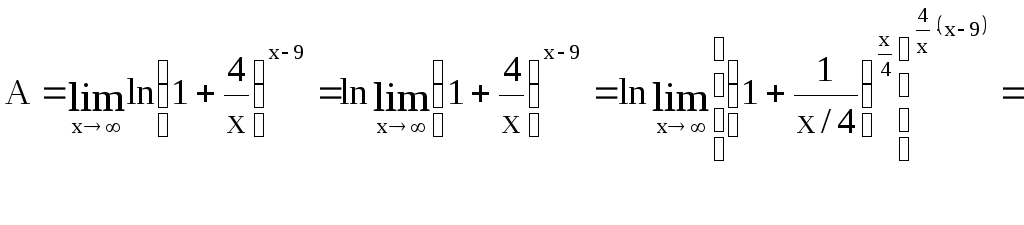
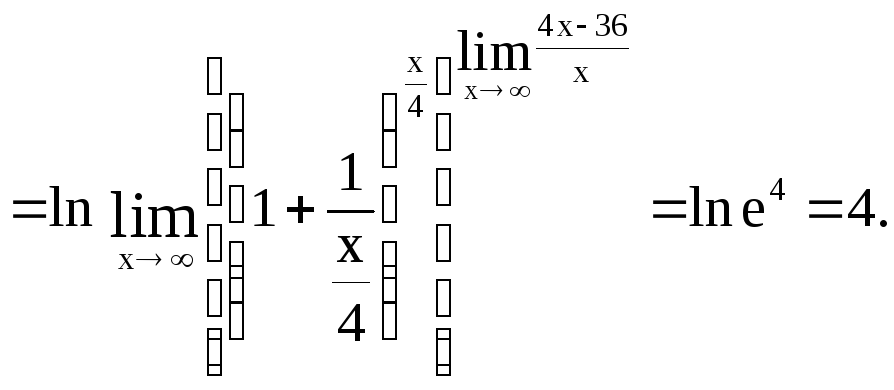
Контрольные варианты к задаче 21
Вычислить пределы функции:
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
8.
|
|
9.
|
10.
|
|
11.
|
12.
|
|
13.
|
14.
|
|
15.
|
16.
|
|
17.
|
18.
|
|
19.
|
20.
|
|
21.
|
22.
|
|
23.
|
24.
|
|
25.
|
26.
|
|
27.
|
28.
|
|
29.
|
30.
|
З а д а ч а 22
Пример 24
Вычислить
![]() .
.
Если
представить предельное значение
переменной х, то получим неопределенность
вида
![]() .
Используя вторую форму второго
замечательного предела
.
Используя вторую форму второго
замечательного предела
![]() ,
введем новую переменную
,
введем новую переменную
![]() .
Тогда
.
Тогда
![]() ,
если
,
если
![]() .
Из замены
.
Из замены
![]() .
Тогда
.
Тогда
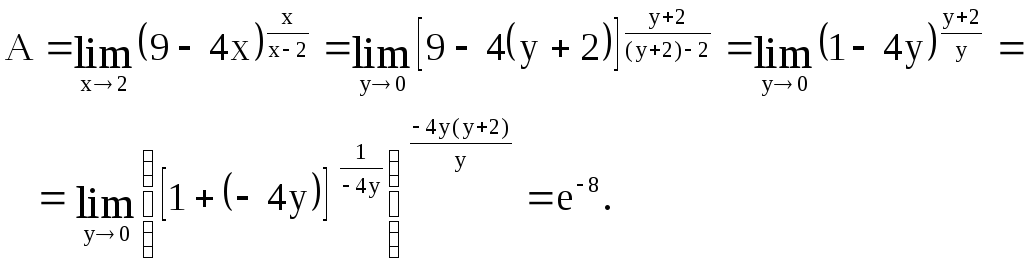
Контрольные варианты к задаче 22
Вычислить пределы функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
З а д а ч а 23
Пример 25
![]() .
.
При
подстановке предельного значения
аргумента возникает неопределенность
![]() .
Приведение к общему знаменателю
сводит эту неопределенность к
.
Приведение к общему знаменателю
сводит эту неопределенность к
неопределенности
![]() или
или
![]() .
.
![]() .
.
