
Операции над векторами Сложение векторов
В алгебраическом представлении при сложении векторов с = a + b проекция результирующего вектора на оси координат является суммой соответствующих проекций складываемых векторов с учётом их знака:
сx = ax + bx ; сy = ay + by ; сz = az + bz .
Если точка привязки не важна, а важна лишь величина (длина) результирующего вектора, то сложение векторов можно считать коммутативной операцией (от перемены мест слагаемых сумма не меняется). В противном случае точка привязки результирующего вектора определяется исходя из физического смысла производимой операции (как правило, в физике точки привязки всех складываемых векторов и суммарного вектора совпадают, — то есть и все слагаемые, и их сумма применимы к одной и той же точке пространства или материальной точке).
Вычитание векторов
Вычитание векторов с = a – b можно представить как сложение уменьшаемого вектора с вектором, противоположным вычитаемому по направлению и равным ему по величине. Таким образом, в агебраическом представлении проекции вычитаемого вектора на оси координат меняют свой знак:
сx = ax – bx ; сy = ay – by ; сz = az – bz .
Умножение вектора на число
При умножении вектора на число b = k · a в алгебраическом виде достаточно все его проекции умножить на это число:
bx = k · ax ; by = k · ay ; bz = k · az .
В строго геометрическом смысле при умножении на число начало вектора остаётся на месте, а «удлиняется» его конец. Однако на физических иллюстрациях часто остаётся на месте точка конца вектора, скажем точка приложения силы, хотя в общем случае этот вопрос всегда определяется физическим смыслом решаемой задачи.
Операция умножения на число является коммутативной a · k = k · a (от перемены мест сомножителей результат не меняется). При положительном множителе результирующий вектор сонаправлен с исходным, при отрицательном направление меняется на строго противоположное. Поэтому результат умножения вектора на число всегда коллинеарен с исходным вектором, за исключением случая, когда множитель или исходный вектор являются нулевыми — тогда результатом будет нулевой вектор, говорить о направлении которого некорректно.
Скалярное произведение векторов
Результатом скалярного перемножения векторов является число, равное произведению их модулей, умноженному на косинус угла между ними.
Вычисление скалярного произведения
В алгебраической форме скалярное произведение d = a · b вычисляется как
d = ax · bx + ay · by + az · bz .
Свойства скалярного произведения
Коммутативность: a · b = b · a .
Дистрибутивность: a · (b + c) = a · b + a · c .
Сочетательность (линейность) относительно скалярного множителя: k · (a · b) = (k · a) · b = a · (k · b) .
Скалярный квадрат вектора равен квадрату его модуля: a · a = |a|2 (норма вектора).
Векторное произведение векторов
|
|
Вычисление векторного произведения
В алгебраической форме векторное произведение c = [a × b] в правой системе координат вычисляется как
сx = ay · bz – az · by ; сy = az · bx – ax · bz ; сz = ax · by – ay · bx .
В левой системе координат знаки слагаемых меняются на противоположные.
В физике обычно подразумевается, что точки привязки всех перемножаемых векторов и результирующего вектора совпадают (и вектора-сомножители, и результат их векторного произведения действуют в одной и той же точке пространства).

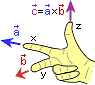 Правая
тройка векторов и правая система
координат.
Правая
тройка векторов и правая система
координат.