Метод Гаусса

Наиболее известным и популярным способом решения линейных систем вида (1) является метод Гаусса. Суть его проста — это последовательное исключение неизвестных. В отличие от курса линейной алгебры, нас будут интересовать вычислительные аспекты метода Гаусса, а именно, технология получения вектора-решения x из исходных матрицы A и вектора b, причем, по возможности, минимизирующая влияние неизбежных ошибок округлений. С этой целью, работая с уравнениями системы (1), выведем сначала совокупность формул, позволяющих в итоге получить искомые значения неизвестных, а затем на их основе запишем алгоритм решения поставленной задачи.

Будем поэтапно приводить систему (1) к треугольному виду, исключая последовательно сначала x₁ из второго, третьего, ..., n-го уравнений, затем x₂ из третьего, четвертого, ..., n-того уравнений преобразованной системы, и т.д.

На первом этапе заменим второе, третье, ... , n-е уравнения на уравнения, получающиеся сложением этих уравнений с первым, умноженным соответственно на , , ..., . Результатом этого этапа преобразований будет эквивалентная (1) система

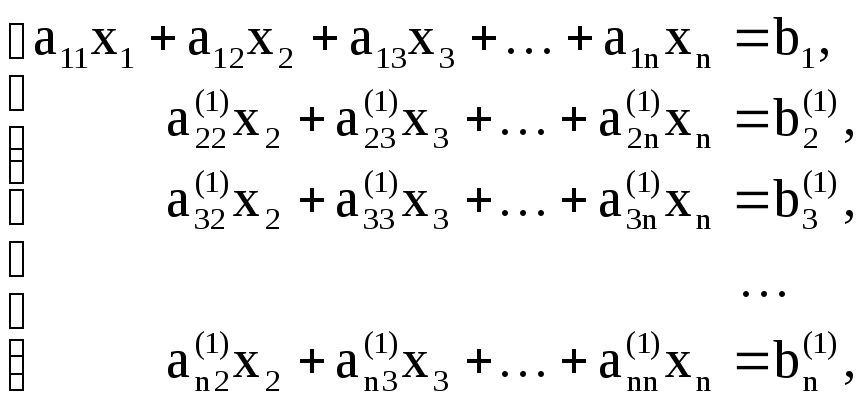(3)

коэффициенты которой (с верхним индексом 1) подсчитываются по формулам

, , где i, j = 2, 3, ..., n.

При этом можно считать, что а₁₁  0, так как по предположению система (1) однозначно разрешима, значит, все коэффициенты при x₁ не могут одновременно равняться нулю, и на первое место всегда можно поставить уравнение с отличным от нуля первым коэффициентом.

На втором этапе проделываем такие же операции, как и на первом, с подсистемой системы (3), получающейся исключением первого уравнения. Эквивалентный (3) (а значит, и (1)) результат второго этапа будет иметь вид

где 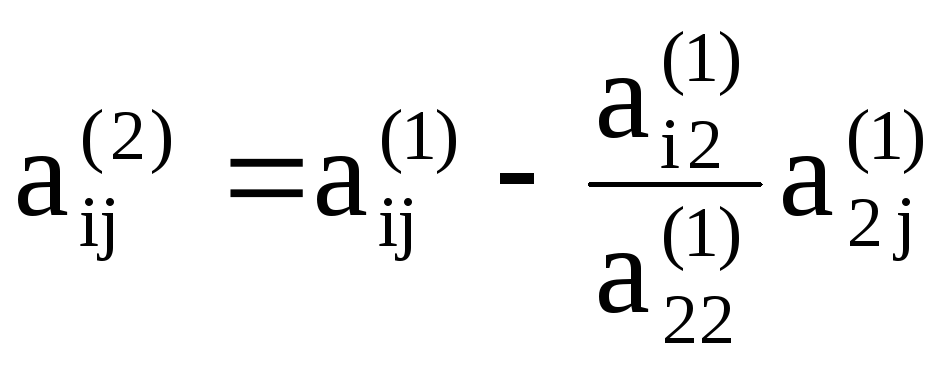, 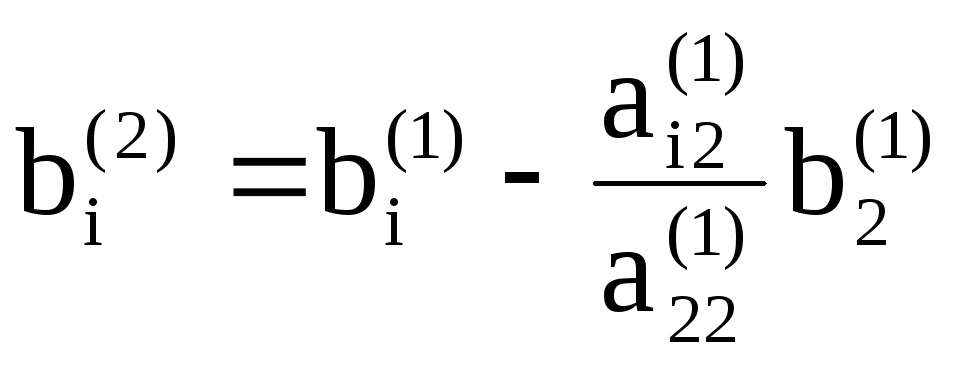; i, j = 3, ..., n.

Продолжая этот процесс, на (n – 1)-м этапе так называемого прямого хода метода Гаусса данную систему (1) приведем к треугольному виду:

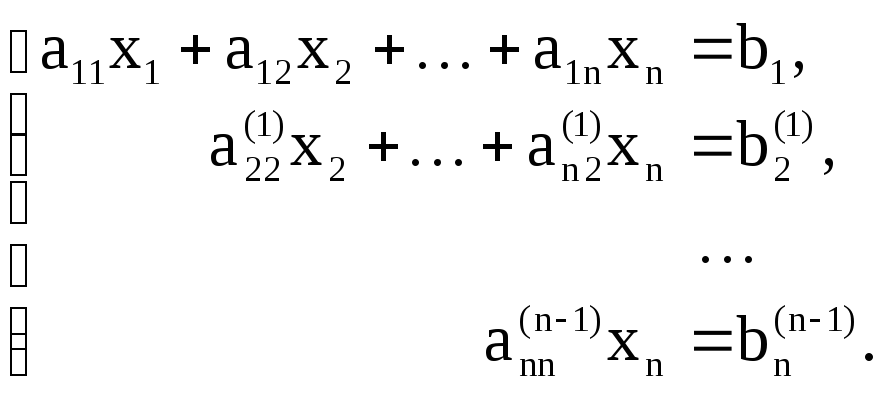(4)

На основе предыдущих рассуждений и формул легко убедиться, что коэффициенты этой системы могут быть получены из коэффициентов данной системы последовательным пересчетом по формулам

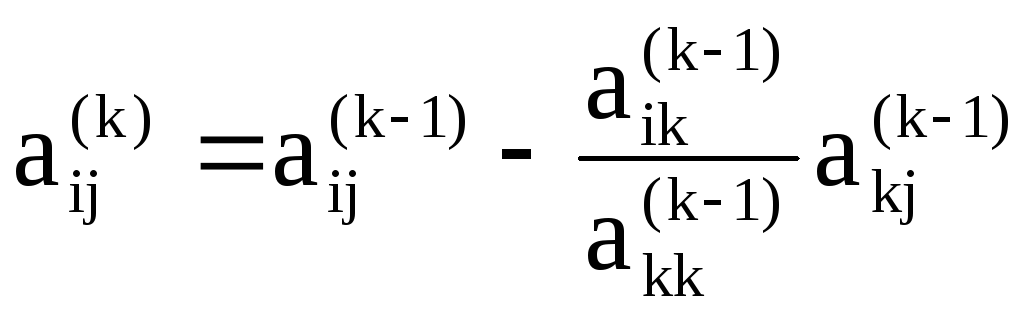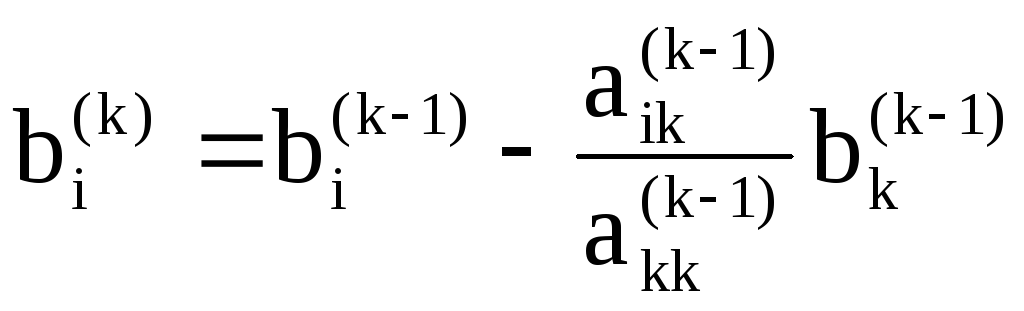, , (5)

где верхний индекс k (номер этапа) должен изменяться от 1 до n – 1, нижние индексы i и j (в любой очередности)— от k + 1 до n; по определению полагаем , .

Треугольная, точнее, трапециевидная структура системы (4) позволяет последовательно одно за другим вычислять значения неизвестных, начиная с последнего:

,

…,

,

.

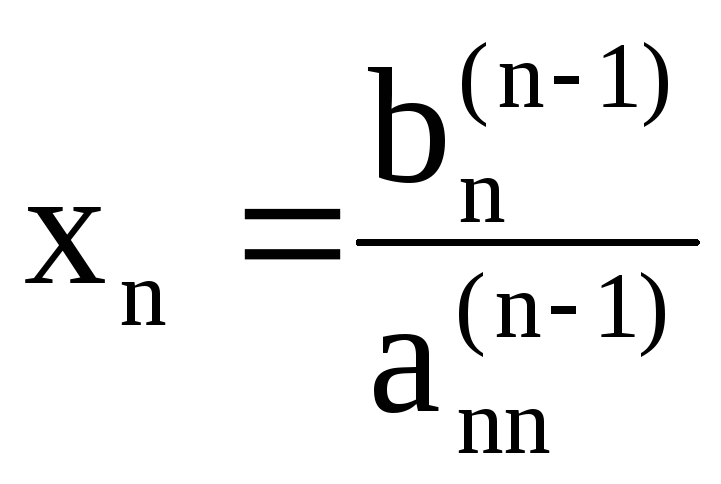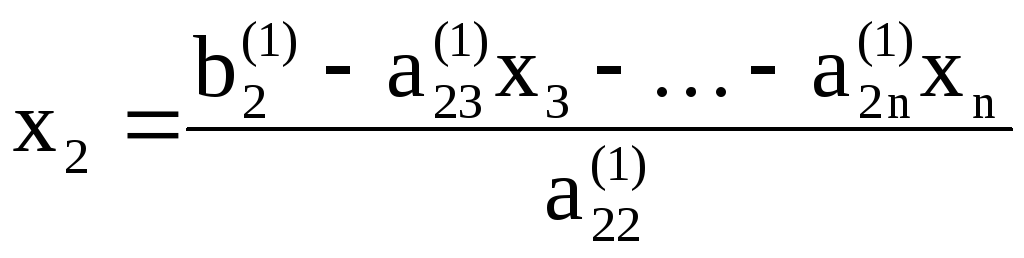Этот процесс последовательного вычисления значений неизвестных называют обратным ходом метода Гаусса. Очевидно, он определяется одной формулой

, (6)

где k полагают равным n, n – 1, ..., 2, 1 и сумма по определению считается равной нулю, если нижний предел суммирования у знака Σ имеет значение больше верхнего.

Итак, решение СЛАУ вида (1) методом Гаусса сводится к последовательной реализации вычислений по формулам (5) и (6).

Итерационные методы Решение слау методом простых итераций

Система стандартного вида

Ax = b, (7)

где — nn-матрица, а x = (x₁, ..., x_n)^Т и b = (b₁, ..., b_n)^Т — n-мерные векторы-столбцы, тем или иным способом (таких способов существует бесконечное множество; некоторые из них будут рассмотрены ниже) может быть преобразована к эквивалентной ей системе вида

x = Bx + с, (8)

где x — тот же вектор неизвестных, а B и c — некоторые новые матрица и вектор соответственно. Систему (8) можно трактовать, как задачу о неподвижной точке линейного отображения B в пространстве Rⁿ и по аналогии со скалярным случаем определить последовательность приближений x^(k) к неподвижной точке x рекуррентным равенством

x^(k+1) = Bx^(k) + с, k = 0, 1, 2, ... (9)

Итерационный процесс (9), начинающийся с некоторого вектора , будем называть методом простых итераций (коротко МПИ).

Изучим комплекс вопросов о сходимости этого процесса. А именно:

1) какие нужно предъявить требования к В, с и x⁽⁰⁾, чтобы последовательность (x^(k)) при k   имела пределом x* — неподвижную точку задачи (8) (и значит, решение эквивалентной (8) исходной системы (7))?

2) с какой скоростью сходится этот процесс, т.е. каков закон убывания абсолютных погрешностей получаемых по формуле (9) приближений?

3) сколько нужно сделать итераций по формуле (9), чтобы при заданном начальном приближении x⁽⁰⁾ найти решение задачи (8) с заданной точностью?

Теорема 1. Необходимые и достаточные условия сходимости МПИ

Необходимым и достаточным условием сходимости метода простых итераций (9) при любом начальном векторе x⁽⁰⁾ к решению x* системы (8) является требование, чтобы все собственные числа матрицы B были по модулю меньше 1.

Теорема 2. Погрешность МПИ

Пусть ||B||  q < 1. Тогда при любом начальном векторе x⁽⁰⁾ МПИ (9) сходится к единственному решению x* задачи (8) и при всех k  N справедливы оценки погрешности:

1) (апостериорная);

2) (априорная).